贝特公式
贝特公式描述了[1] 带电粒子(质子,粒子,离子)穿越介质单位距离时的平均能损,即材料的阻止本领。 对于电子来说,其能损稍有不同,主要是由于其质量较小(要求相对论更正)以及其全同性,并且由于电子的轫致辐射损失能量较多,因此也需要将这一项考虑在内。快速的带电粒子穿过材料时,与材料中原子的电子发生相互作用,从而激发或者电离材料原子,这一相互作用导致粒子的能量损失。
非相对论的贝特公式由汉斯·贝特在1930年发现,而相对论版(见下文)由他在1932年发现[2]。注意平均能损不同于最可几能损,后者由郎道-瓦维洛夫理论描述。[3]
贝特公式有时被称为贝特-布洛赫公式,但这是一种误导(见下文)。
公式内容
速度为,电荷数为(整数,单位为基本电荷),能量为的带电粒子,在电子数密度为,平均激发能为的材料中穿越距离时,在国际单位制中,相对论版的贝特公式为:[2]
-
()
其中c 是光速,为真空介电常数, , 和 为基本电荷和电子的静质量。
材料的电子数密度可以通过下面公式来计算:
其中 是材料的密度, 是材料的原子序数, 是相对原子质量, 是阿伏伽德罗常数, 为摩尔质量常数。
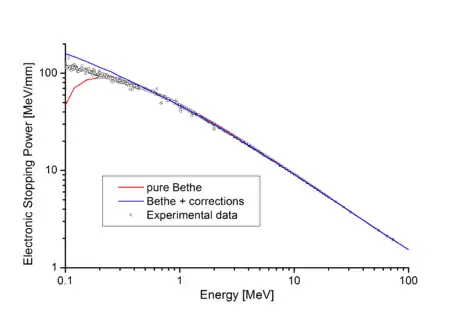
在右图中,黑色圆圈是不同作者给出的实验测量结果,红色曲线是未修正的贝特公式。[4] 显然,贝特公式在高能区很好地符合了实验结果。 当添加了一些修正项后,贝特公式符合得更好(图中的蓝色曲线,见下文)。
对于低能带电粒子,即相对速度 ,贝特公式简化为
-
()
这可以从 (1)式中将 由 替代,并忽略其余 项得到。
在低能区,根据贝特公式,粒子的能损随 的增加而降低,并在 达到最小值,其中 是粒子的质量(对于质子来说,该极值点约为3000 MeV)。 在极端相对论的情况下,,粒子的能损对数增加,这主要是由于电场的横向分量造成的。
参考文献
- H. Bethe und J. Ashkin in "Experimental Nuclear Physics, ed.
- Sigmund, Peter Particle Penetration and Radiation Effects.
- H. Bichsel, Rev.
- . 2015-04-15 [2015-11-01]. (原始内容存档于2012-02-06).