邊 (圖論)
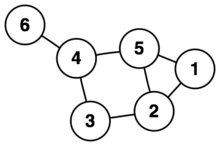
在圖論中,邊(edges)是圖的基本單元之一,其與點共同組成了圖。一般的情況下,邊通常是連接兩個點的圖論元素,而在部分的情況下會只連接1個點(如非簡單圖)或連接3個或更多個點(如超圖),因此邊通常可以被定義為將點相連的元素,而被邊連接的點稱為端點。
分類
邊依照連接的點數量可以分為三類,其中一種稱為簡單邊,即這些邊連接2個相異的點。簡單圖的每一個邊皆為簡單邊。另一種為超邊(hyperedges),即這些邊連接3個或更多個點,通常出現於超圖中,其也可以依照其連接的邊數稱為多元邊,例如連接三個點的邊可稱為三元邊。另一類為只連接1個點的邊,或連接的兩點是相同點的邊,這種邊通常稱為自環。
簡單邊
在圖論中,簡單邊是指連接2個相異點的邊。簡單圖的每一個邊皆為簡單邊。更正式地,簡單邊可以定義為,有一個圖是一個二元組,其中是點集、是邊集,並且滿足,由所有無序點對構成(換句話說,邊連接了兩相異點),而這個連接了此兩個相異點的邊則稱為簡單邊。[1][2]
超邊
在圖論中,超邊又稱超連結(hyperlinks)、接口或連接(connectors)[3] 是指連接任意數量點的邊,其連接的點數量不一定為2個,可能是3個或更多。更正式地,超邊可以定義為,有一個超圖是一個二元組,其中是點集、是邊集,且邊集是的子集、是的冪集,而中的邊稱為超邊。
在不同領域中,超邊有許多不同的名稱,例如,在計算幾何學中,超邊又可以被稱為範圍(ranges)[4]、在合作博弈論中,超邊又可稱為簡單博弈(simple games)[5]。
無向邊
若一個邊不具有方向性,則稱該邊為無向邊,其可以視為2個點的集合,或只有2個點的超邊。無向邊也可以在有向圖中存在,即雙向連結都存在的邊,例如有兩點A和B,若同時存在A到B的邊和B到A的邊,則這條邊在這個有向圖中可以稱為一個無向邊。
與幾何學的關聯
在圖論中的邊與幾何學的邊不同,圖論中的邊是指連接點的抽象,不同於多邊形、多面體等幾何圖形的邊,幾何圖形的邊通常具有具體的線段或曲線,而圖論中的邊僅表達了哪些頂點要相連,哪些不用。[14]
參見
參考文獻
- Bender, Edward A.; Williamson, S. Gill. . 2010 [2019-09-14]. (原始内容存档于2020-10-19).
- See, for instance, Iyanaga and Kawada, 69 J, p. 234 or Biggs, p. 4.
- Judea Pearl, in HEURISTICS Intelligent Search Strategies for Computer Problem Solving, Addison Wesley (1984), p. 25
- Haussler, David; Welzl, Emo, , Discrete and Computational Geometry, 1987, 2 (2): 127–151, MR 0884223, doi:10.1007/BF02187876
- Peleg, B. . . Handbook of Social Choice and Welfare 1. 2002: 195–201. ISBN 9780444829146. doi:10.1016/S1574-0110(02)80012-1.
- Balakrishnan, V. K.; Graph Theory, McGraw-Hill; 1 edition (February 1, 1997). ISBN 0-07-005489-4
- Bollobás, Béla; Modern Graph Theory, Springer; 1st edition (August 12, 2002). ISBN 0-387-98488-7
- Diestel, Reinhard; Graph Theory, Springer; 2nd edition (February 18, 2000). ISBN 0-387-98976-5
- Gross, Jonathon L, and Yellen, Jay; Graph Theory and Its Applications, CRC Press (December 30, 1998). ISBN 0-8493-3982-0
- Gross, Jonathon L, and Yellen, Jay; (eds); Handbook of Graph Theory. CRC (December 29, 2003). ISBN 1-58488-090-2
- Zwillinger, Daniel; CRC Standard Mathematical Tables and Formulae, Chapman & Hall/CRC; 31st edition (November 27, 2002). ISBN 1-58488-291-3
- Beineke, Lowell W.; Wilson, Robin J., , Encyclopedia of Mathematics and its Applications 128, Cambridge University Press, Cambridge: 5, 2009, ISBN 978-0-521-80230-7, MR 2581536, doi:10.1017/CBO9781139087223
- G. Gallo, G. Longo, S. Nguyen, S. Pallottino, Directed hypergraphs and applications, DOI link, Citeseer link.
- Senechal, Marjorie, , Springer: 81, 2013 [2019-09-14], ISBN 9780387927145, (原始内容存档于2014-01-07).
