连通分量标记
连通分量标记(或者称连通分量分析,连通区域标记)是图论应用中的一种算法,给二值图像中的每个连通区域标上一个特定的标号。该算法可用来对图像的目标进行定位和计数。该算法不要和图像分割相混淆。
连通分量标记通常在计算机视觉领域中对二值图像的连通区域进行检测,也可以处理彩色图像和更高维的数据。[1][2]当将其集成到图像识别系统或者是人机交互系统时,该算法也起到重要作用。[3][4]
概述

4-邻域

8-邻域
中间像素和它周围像素的位置决定了是几邻域连接,4邻域连接是周围像素处在中间像素的上下左右的位置,8邻域连接则还包括其对角的4个像素的位置。
算法
两次扫描算法的图形解释
以一个8领域的例子来说明两次扫描算法。 该算法的数据结构为并查集。 1,第一次扫描: 将0视为背景像素,1为目标像素。原始图像如下。
![]()
从左往右从上到下扫描,背景像素保持0不变,遇到1值时,分析它的8邻域(只考虑已被扫描的的像素点,即左边、左上、上和右上这四个方向的像素值)
- 如果这四个方向的值都是0,那么该位置就创建一个新的标号(在原标号上加1);
- 如果这四个方向的非0值(即标号)都一样,那么该位置标号就是其领域的非0标号;
- 如果这四个方向的非0值有两个不同的标号,那么该位置标号就选其中之一,并记录这两个不同的标号(因为这两个标号是连通的,故视为等同的标号);
第一次扫描结束后得到如下标好号的图:
![]()
并且同时得到哪些标号相同的。
| Set ID | Equivalent Labels |
|---|---|
| 1 | 1,2 |
| 2 | 1,2 |
| 3 | 3,4,5,6,7 |
| 4 | 3,4,5,6,7 |
| 5 | 3,4,5,6,7 |
| 6 | 3,4,5,6,7 |
| 7 | 3,4,5,6,7 |
2,第二次扫描: 合并这些相同的标号,得到结果
![]()
最后可以将这两个区域以不同颜色显示出来
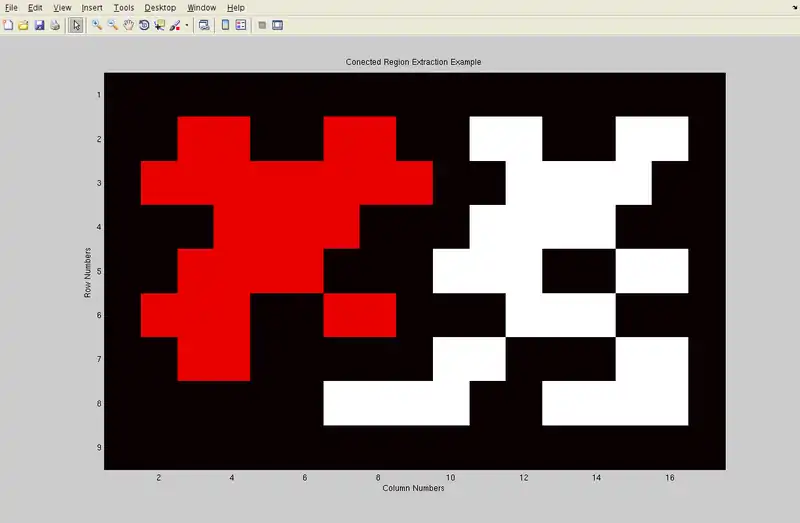
其伪代码如下:
algorithm TwoPass(data)
linked = []
labels = structure with dimensions of data, initialized with the value of Background
First pass
for row in data:
for column in row:
if data[row][column] is not Background
neighbors = connected elements with the current element's value
if neighbors is empty
linked[NextLabel] = set containing NextLabel
labels[row][column] = NextLabel
NextLabel += 1
else
Find the smallest label
L = neighbors labels
labels[row][column] = min(L)
for label in L
linked[label] = union(linked[label], L)
Second pass
for row in data
for column in row
if data[row][column] is not Background
labels[row][column] = find(labels[row][column])
return labels
参考文献
- H. Samet and M. Tamminen. . IEEE Transactions on Pattern Analysis and Machine Intelligence (TIEEE Trans. Pattern Anal. Mach. Intell.). 1988, 10 (4): 579. doi:10.1109/34.3918.
- Michael B. Dillencourt and Hannan Samet and Markku Tamminen. . Journal of the ACM (J. ACM). 1992, 39 (2): 253. doi:10.1145/128749.128750.
- Weijie Chen, Maryellen L. Giger and Ulrich Bick. . Academic Radiology. 2006, 13 (1): 63–72. PMID 16399033. doi:10.1016/j.acra.2005.08.035.
- Kesheng Wu, Wendy Koegler, Jacqueline Chen and Arie Shoshani. . SSDBM. 2003 [2016-04-04]. (原始内容存档于2008-09-06).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.