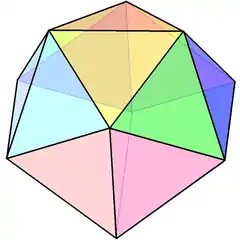
邊收縮二十面體

在幾何學中，邊收縮二十面體是一種凸多面體，是指將正二十面體的其中1條邊作邊收縮變換後所產生的多面體，由18個三角形面、27條邊和11個頂點構成，擁有四階的C2v循環群對稱性，屬於三角面多面體，是十八面體中的一個特例。

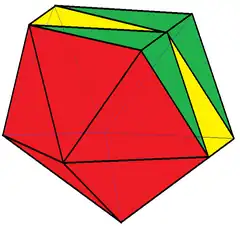邊收縮二十面體
邊收縮二十面體
（點選觀看旋轉模型）
類別三角面多面體
性質
面18
邊27
頂點11
歐拉特徵數F=18, E=27, V=11 （χ=2）
組成與佈局
面的種類三角形×18
面的佈局
2 (34)
8 (35)
1 (36)
對稱性
對稱群C2v, [2], (*22), order 4
特性
凸、 三角面
圖像

（展開圖）

雖然邊收縮二十面體的面分布得很均勻，但不具有球體的對稱性。一般来说，面分布均勻的多面體的形狀會接近球体，但邊收縮二十面體却不具有此種特性。此外，具有這種結構的嚴格凸多面体的邊不能等長，因為有部分頂點為6三角形的公共頂點，若其為正三角形，則會造成这6個面共面，而無法组成嚴格凸多面體[1][註 1]。因此，邊收縮二十面體亦可歸類為擬詹森多面體。

性質

在幾何學中，邊收縮二十面體有18個面、27個邊和11個頂點，因此它的對偶多面體是一個十一面體。它屬於凸多面體，因此歐拉示性數為2。

從展開圖可以看出，該多面體共有三种不同的面，面積都很接近。

相關幾何圖形

正切割二十面體

正切割二十面體是將正二十面體中適當的6個面每三個面為一組地替換為梯形而形成的多面體，其性質與邊收縮的二十面體性質類似。

正切割二十面體由13個面、23條邊和10個頂點組成。13個面中，有11正三角形和2個梯形[2]。

在化學領域

在化學中，將十八面體硼烷離子（[B11H11]2−）中的氫全部去掉後，可以得到这种多面体的幾何結構。


十八面體硼烷 [B11H11]2−
展開圖

註釋
  1. 嚴格凸多面體的要求為：各角的角度均嚴格小於180度，且各個面皆不共面。

參考文獻
  1. Holleman, Arnold Frederik; Wiberg, Egon, Wiberg, Nils , 编, , 由Eagleson, Mary; Brewer, William翻译, San Diego/Berlin: Academic Press/De Gruyter: 1165, 2001, ISBN 0-12-352651-5
  2. John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26) The Grand Antiprism

外部連結
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.