铁木辛柯梁理论
铁木辛柯梁是20世纪早期由美籍俄裔科学家与工程师斯蒂芬·铁木辛柯提出并发展的力学模型。[1][2]模型考虑了剪应力和转动惯性,使其适于描述短梁、层合梁以及波长接近厚度的高频激励时梁的表现。结果方程有4阶,但不同于一般的梁理论,如欧拉-伯努利梁理论,还有一个2阶空间导数呈现。实际上,考虑了附加的变形机理有效地降低了梁的刚度,结果在一稳态载荷下挠度更大,在一组给定的边界条件时预估固有频率更低。后者在高频即波长更短时效果更明显,反向剪力距离缩短时也有同样效果。
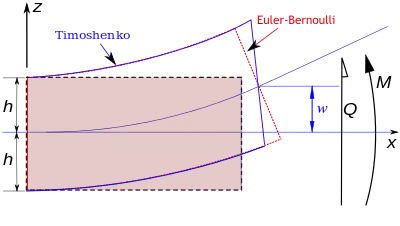
控制方程
准静态铁木辛柯梁
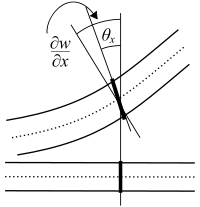
在静力学中铁木辛柯梁理论没有轴向影响,假定梁的位移服从于
式中是梁上一点的坐标,是位移矢量的三维坐标分量,是对于梁的中性面的法向转角,是中性面的在方向的位移。
控制方程是以下常微分方程的解耦系统:
静态条件下的铁木辛柯梁理论,若在以下條件成立時,等同于欧拉-伯努利梁理论
此時,可忽略上面控制方程的最后一项,得到有效的近似,式中是梁的长度。
对于等截面均匀梁,合并以上两个方程,
动态铁木辛柯梁
在铁木辛柯梁理论中若不考虑轴向影响,则给出梁的位移
式中是梁内一点的坐标,是位移矢量的三维坐标分量,是对于梁的中性面的法向转角,是中性面方向的位移.
从以上假设,铁木辛柯梁,考虑到振动,要用线性耦合偏微分方程描述:[3]
其中因变量是梁的平移位移和转角位移。注意不同于欧拉-伯努利梁理论,转角位移是另一个变量而非挠度斜率的近似。此外,
这些参数不一定是常数。
对于各向同性的线弹性均匀等截面梁,以上两个方程可合并成[4][5]
轴向影响
如果梁的位移由下式给出
其中是方向的附加位移,则铁木辛柯梁的控制方程成为
其中,是外加轴向力。任意外部轴向力的平衡依靠应力
式中是轴向应力,梁的厚度设为。
包含轴向力的梁方程合并为
阻尼
如果,除轴向力外,我们考虑与速度成正比的阻尼力,形如
铁木辛柯梁的耦合控制方程成为
合并方程为
切变系数
确定切变系数不是直接的,一般它必须满足:
切变系数由泊松比确定。更严格的表达方法由多位科学家完成,包括斯蒂芬·铁木辛柯、雷蒙德·明德林(Raymond D. Mindlin)、考珀(G. R. Cowper)和约翰·哈钦森(John W. Hutchinson)等。工程实践中,斯蒂芬·铁木辛柯的表达一般状况下足够好。[6]
对于固态矩形截面:
对于固态圆形截面:
参考文献
- Timoshenko, S. P., 1921, On the correction factor for shear of the differential equation for transverse vibrations of bars of uniform cross-section, Philosophical Magazine, p. 744.
- Timoshenko, S. P., 1922, On the transverse vibrations of bars of uniform cross-section, Philosophical Magazine, p. 125.
- . [2013-03-22]. (原始内容存档于2007-10-15).
- Thomson, W. T., 1981, Theory of Vibration with Applications
- Rosinger, H. E. and Ritchie, I. G., 1977, On Timoshenko's correction for shear in vibrating isotropic beams, J. Phys. D: Appl. Phys., vol. 10, pp. 1461-1466.
- Stephen Timoshenko, James M. Gere. Mechanics of Materials. Van Nostrand Reinhold Co., 1972. Pages 207.
- Stephen P. Timoshenko. . Verlag von Julius Springer. 1932.