铅垂线
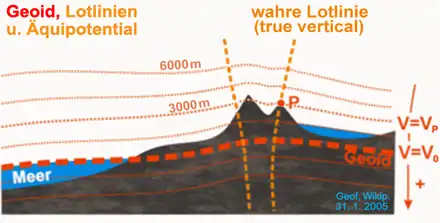
铅垂线(英語:),又称垂线或力线[1]:29,在大地测量学中指重力作用的方向线[2]:142[3]:8。铅垂线与与重力矢量的方向处处相切,该方向又被称为铅垂方向,有时也直接以铅垂线代称。[4]:48-50在重力场中,铅垂线通常是曲线而非直线,彼此互不平行,与其经过的重力等位面正交。[4]:50铅垂线与参考椭球面的法线之间的方向偏差被称为垂线偏差。[4]:83
曲率
由于在重力场中,除轴线外,同一直线上各点的重力矢量方向通常各不相同。因此,铅垂线通常是一条具有曲率的曲线。通过计算铅垂线的曲率,可以将地形表面上进行的天文测量数据归算到大地水准面上。[4]:53铅垂线在某点处的曲率 可以通过该点处的重力矢量的大小 及其一阶微分 、 得到:[4]:54
参考文献
- 孔祥元; 郭际明; 刘宗泉. . 武汉大学出版社. 2001. ISBN 978-7-30-707562-7.
- Lu, Zhiping; Qu, Yunying; Qiao, Shubo. . Springer. 2014-05-23 [2020-04-05]. ISBN 978-3-642-41245-5. (原始内容存档于2020-06-12) (英语).
- . 清华大学出版社有限公司. 2001: 8 [2020-04-05]. ISBN 978-7-302-04717-9. (原始内容存档于2020-06-12) (中文).
- San Francisco W. H. Freeman and Company. . San Francisco: W. H. Freeman and Company. 1967.
- 潘正风; 程效军; 成枢; 王腾军; 翟翊. . 武汉大学出版社. 2015-07-01. ISBN 978-7-307-15677-7.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.