倒數伽瑪函數
在數學中,倒數伽瑪函數(英語:Reciprocal gamma function)是指伽瑪函數的倒數:
Γ函數的倒數
Γ函數(藍色)、Γ函數的倒數(橘色)
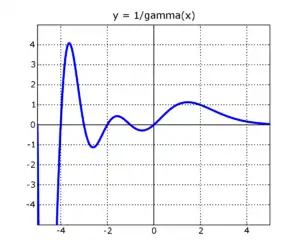
Γ函數的倒數的函數圖形
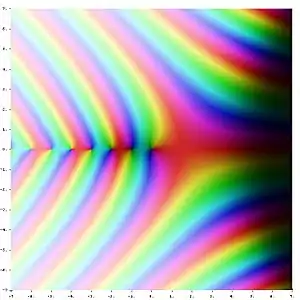
倒數伽瑪函數 1/Γ(z) 的色相環複變函數圖形
其中,Γ(z)代表伽瑪函數。由於伽瑪函數在整個複數平面上皆非零且為亚纯函数,因此其倒數是一個整函数。
倒數伽瑪函數是一個1階整函數,其表示了log log |1/Γ(z)|的成長速度不會高過log |1/Γ(z)|。雖為1階整函數但屬無窮型,也就是說log |1/Γ(z)|的增長速度比任何|z|的倍數都快,因為它的增長與左手平面上的|z| log |z|大致成比例。
由於倒數伽瑪函數不像伽瑪函數快速成長,在程式計算上較伽瑪函數容易,例如其泰勒級數[1],因此部分軟體使用倒數伽瑪函數作為計算伽瑪函數的起點,一些軟體除了計算伽瑪函數外,會額外提供倒數伽瑪函數。
魏爾斯特拉斯將倒數伽瑪函數稱為「factorielle」表示階乘的倒數,並用於魏尔施特拉斯分解定理的發展[2]。
泰勒級數
倒數伽瑪函數從零展開的泰勒級數為:
其中γ是歐拉-馬斯刻若尼常數。對n > 2的情形,其zn的系數an可由遞迴定義求出[3]:
其中ζ(s)代表黎曼ζ函數。2014年,Fekih-Ahmed發現這些係數可以用積分表示[1]:
其前幾項的值為:
| n | an |
|---|---|
| 1 | +1.0000000000000000000000000000000000000000 |
| 2 | +0.5772156649015328606065120900824024310422 |
| 3 | −0.6558780715202538810770195151453904812798 |
| 4 | −0.0420026350340952355290039348754298187114 |
| 5 | +0.1665386113822914895017007951021052357178 |
| 6 | −0.0421977345555443367482083012891873913017 |
| 7 | −0.0096219715278769735621149216723481989754 |
| 8 | +0.0072189432466630995423950103404465727099 |
| 9 | −0.0011651675918590651121139710840183886668 |
| 10 | −0.0002152416741149509728157299630536478065 |
| 11 | +0.0001280502823881161861531986263281643234 |
| 12 | −0.0000201348547807882386556893914210218184 |
| 13 | −0.0000012504934821426706573453594738330922 |
| 14 | +0.0000011330272319816958823741296203307449 |
| 15 | −0.0000002056338416977607103450154130020573 |
| 16 | +0.0000000061160951044814158178624986828553 |
| 17 | +0.0000000050020076444692229300556650480600 |
| 18 | −0.0000000011812745704870201445881265654365 |
| 19 | +0.0000000001043426711691100510491540332312 |
| 20 | +0.0000000000077822634399050712540499373114 |
| 21 | −0.0000000000036968056186422057081878158781 |
| 22 | +0.0000000000005100370287454475979015481323 |
| 23 | −0.0000000000000205832605356650678322242954 |
| 24 | −0.0000000000000053481225394230179823700173 |
| 25 | +0.0000000000000012267786282382607901588938 |
| 26 | −0.0000000000000001181259301697458769513765 |
| 27 | +0.0000000000000000011866922547516003325798 |
| 28 | +0.0000000000000000014123806553180317815558 |
| 29 | −0.0000000000000000002298745684435370206592 |
| 30 | +0.0000000000000000000171440632192733743338 |
而an的近似值為[1]:
其中,
- 而是分支為負一的朗伯W函数。
階乘倒數
階乘倒數是指階乘的倒數。其等於所有小於及等於該數的正整數之倒數的積:
由於階乘可以用伽瑪函數來定義,因此階乘倒數也可以表示為:
- .
對於的正整數,其階乘倒數可以用一個積分表示[6] :
- .
同理,倒數伽瑪函數也可以用類似的方法表示。對所有的實數 且 ,我們可以寫出倒數伽瑪函數沿著實軸的積分表示式[7]:
其中在的特定情況下,則可獲得雙階乘的倒數與倒數伽瑪函數之關係:
參考文獻
- Fekih-Ahmed, L. (2014). On the Power Series Expansion of the Reciprocal Gamma Function (页面存档备份,存于) (PDF). [2018-12-22]. (原始内容存档 (PDF)于2018-12-22).. HAL archives,
- Hazewinkel, Michiel (编), , , Springer Science+Business Media B.V. / Kluwer Academic Publishers, 2001 [1994], ISBN 978-1-55608-010-4
- Wrench, J.W. (1968). Concerning two series for the gamma function. Mathematics of Computation, 22, 617–626. and
Wrench, J.W. (1973). Erratum: Concerning two series for the gamma function. Mathematics of Computation, 27, 681–682. - . [2018-12-28]. (原始内容存档于2019-06-10).
- Fourth, Tokyo: Iwanami Shoten, 2007, ISBN 978-4-00-080309-0, MR 2383190 (日语) 142.D
- Graham, Knuth, and Patashnik. . Addison-Wesley. 1994: 566.
- . Math Stack Exchange. [2018-11-18]. (原始内容存档于2019-06-06).
- Finch, S. R. "Fransén-Robinson Constant." §4.6 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 262-264, 2003.
- Thomas Schmelzer & Lloyd N. Trefethen, Computing the Gamma function using contour integrals and rational approximations
- Mette Lund, An integral for the reciprocal Gamma function (页面存档备份,存于)
- Milton Abramowitz & Irene A. Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables
- Eric W. Weisstein, Gamma Function(页面存档备份,存于), MathWorld
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.