韋爾—費倫結構

在幾何學中，韋爾—費倫結構[1]是一種較複雜的三維結構，其代表了大小相等的氣泡所形成的理想化泡沫結構之一。1993年都柏林大學三一學院的物理學家丹尼斯·韦尔和罗伯特·费伦用電腦模擬泡沫結構發現韋爾—費倫結構是克耳文問題裡比克耳文結構更好的解。這種結構被用於北京市国家游泳中心建築水立方的設計中。

韋爾—費倫結構
類型堆砌
維度3
考克斯特記號
2o
纖維流形記號[[4,3,4]+]
性質
胞五角十二面體
空間填充十四面體
面五邊形
六邊形
對稱性
空間群Pm3n (223)
特性
胞等體積

歷史

克耳文1887年提出了一個問題：如何將空間劃分為一系列等體積的胞，且每個胞的表面積最小。簡而言之，效率最高的泡沫結構是什麼？[2]這個問題被稱為克耳文問題。

克耳文提出了一種基於截角八面體堆砌的泡沫結構，因此截角八面體堆砌又被稱為克耳文結構。截角八面體堆砌是一種由截角八面體獨立填滿三維空間的幾何結構，是凸均勻堆砌體的一種，其中截角八面體是一個空間填充十四面體，由6個正方形面和8個正六邊形面組成。為了使其符合泡沫的經驗定律普拉托定律[3][4]，克耳文結構中的截角八面體之六邊形面有略微彎曲。

截角八面體堆砌是立方體經過過截角變換後的像。克耳文猜想這個結構是克耳文問題的最佳解，即經過截角變換後的立方體堆砌是效率最高的泡沫結構。這個猜想被廣泛接受，且100年後才發現反例，該反例為韋爾—費倫結構。[5]

2009年，魯格羅・加布里埃利（Ruggero Gabbrielli）[6]發表了一種使用斯威夫特–奧昂貝格方程在最小曲面上找到克耳文問題候選解的方法。[7][8]

性質

韋爾—費倫結構與克耳文結構的皆具有每個胞體積相同的特性，其不同之處在於克耳文結構每個胞皆全等而韋爾—費倫結構是由2種不同形狀的胞組合而成。[5][9]

胞的組成

韋爾—費倫結構由兩種胞組成。從拓撲學與對稱性的角度來看，韋爾—費倫結構的其中一個組成胞是五角十二面體，其為黃鐵礦的一種晶體形狀，外觀類似正十二面體，但不是正多面體，並具有五角十二面體群的對稱性（Th，一種四面體對稱的變體）[5]。

另外一個組成胞為一種類似截對角六方偏方面體的形狀，是一種由2個六邊形和12個五邊形組成的十四面體，這種形狀有時稱為戈柏十四面體（Goldberg polyhedron）[5]。


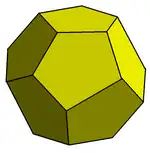五角十二面體
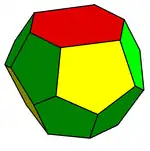類似截對角六方偏方面體的空間填充十四面體

泡沫結構

類似於克耳文結構中的六邊形略微彎曲的狀況，韋爾—費倫結構中兩種胞的五邊形面也略微彎曲。韋爾—費倫結構的表面積比克耳文結構還要小0.3%，不過尚未有研究證實韋爾—費倫結構是克耳文問題的最佳解。部分實驗表明，在有利的邊界情況下，每個胞等體積的泡沫結構會自組裝為 原子位置與韋爾—費倫結構中的多面體胞之幾何中心重合的A15相[10][11]。

多面體結構

直接將上述兩種多面體堆砌起來的幾何結構也稱為韋爾—費倫結構，其與前述結構差異在於，前述的韋爾—費倫結構面有彎曲，而若是在描述多面體堆砌體時，則會是討論面皆為平面的狀況。這種多面體堆砌結構在對應的泡沫結構被提出前就已經被發現了，然而發現當初尚未與克耳文問題做結合。[12]

在化學中，這種結構以及其兩種胞的形狀皆可以在晶體學中找到。若晶體的單元位於多面體的幾何中心則可以形成一種弗蘭克-卡巴斯爾相[13][14]。

應用
2008年北京奧運水上項目比賽場館的国家游泳中心建築水立方。

被用於2008年北京奧運水上項目比賽場館的国家游泳中心建築水立方的外觀氣泡設計靈感來自韋爾—費倫結構[15][1]，其設計出的結構支撐系統不但很堅固也很輕巧。由於結構中所有的接縫都接近四面角，因此該框架用了很少的材料就能填滿很大的空間，就像是二維的六邊形蜂巢結構那樣。[16][17][18]

參見

參考文獻
  1. Ellery B. Golos; Daniel D. Joseph. . Prindle, Weber & Schmidt. 1981. ISBN 978-0-87150-301-5.
  1. . china.com.cn. 2004-05-14 [2019-09-29]. （原始内容存档于2004-09-05）.
  2. Lord Kelvin (Sir William Thomson), (PDF), Philosophical Magazine, 1887, 24 (151): 503 [2019-09-29], doi:10.1080/14786448708628135, （原始内容存档 (PDF)于2021-11-26）.
  3. Jean E. Taylor. "The Structure of Singularities in Soap-Bubble-Like and Soap-Film-Like Minimal Surfaces". Annals of Mathematics, 2nd Ser., Vol. 103, No. 3. May, 1976, pp. 489–539.
  4. Frederick J. Almgren Jr and Jean E. Taylor, “The geometry of soap films and soap bubbles”, Scientific American, vol. 235, pp. 82–93, July 1976.
  5. . steelpillow.com. [2019-09-29]. （原始内容存档于2019-08-06）.
  6. Gabbrielli, Ruggero. . scholar.google.com.
  7. Gabbrielli, Ruggero. . Philosophical Magazine Letters. 2009-08-01, 89 (8): 483–491. ISSN 0950-0839. doi:10.1080/09500830903022651.
  8. Freiberger, Marianne. . Plus Magazine (University of Cambridge). 2009-09-24 [2017-07-04]. （原始内容存档于2019-09-29） （英语）.
  9. Șerban, D. A., Sărăndan, S., Negru, R., Belgiu, G., & Marşavina, L., , IOP Conference Series: Materials Science and Engineering 416 (1) (IOP Publishing), 2018, 416 (1): 012108
  10. Gabbrielli, R.; Meagher, A.J.; Weaire, D.; Brakke, K.A.; Hutzler, S., , Phil. Mag. Lett., 2012, 92: 1–6, doi:10.1080/09500839.2011.645898.
  11. Ball, Philip, , Nature, 2011, doi:10.1038/nature.2011.9504.
  12. A diagram can be found in Pauling, Linus. 3rd. Cornell University Press. 1960: 471., as shown on Ken Brakke's page （页面存档备份，存于）.
  13. Frank, F. C.; Kasper, J. S., (PDF), Acta Crystallogr., 1958, 11 (3): 184–190 [2019-09-29], doi:10.1107/s0365110x58000487, （原始内容存档 (PDF)于2021-08-31）
  14. Frank, F. C.; Kasper, J. S., , Acta Crystallogr., 1959, 12 (7): 483–499, doi:10.1107/s0365110x59001499.
  15. Fountain, Henry, , New York Times, 2008-08-05 [2019-09-29], （原始内容存档于2019-08-22）.
  16. . BBC Sports. [2019-09-29]. （原始内容存档于2019-10-18）.
  17. Peter Rogers. . 2004-05-06 [2019-09-29]. （原始内容存档于2019-09-29）.
  18. Pearson, Clifford. . Architectural Record (McGraw Hill). July 2008, 196 (7) [2008-08-16]. （原始内容存档于2008-08-13）.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.