泰勒级数
在数学中,泰勒级数(英語:)用无限项连加式——级数来表示一个函数,这些相加的项由函数在某一点的导数求得。泰勒级数是以于1715年发表了泰勒公式的英國数学家布魯克·泰勒()来命名的。通过函数在自变量零点的导数求得的泰勒级数又叫做麦克劳林级数,以苏格兰数学家科林·麦克劳林的名字命名。
拉格朗日在1797年之前,最先提出帶有餘項的現在形式的泰勒定理。实际应用中,泰勒级数需要截断,只取有限项,可以用泰勒定理估算这种近似的误差。一个函数的有限项的泰勒级数叫做泰勒多项式。一个函数的泰勒级数是其泰勒多项式的极限(如果存在极限)。即使泰勒级数在每点都收敛,函数与其泰勒级数也可能不相等。在开区间(或复平面上的开区间)上,与自身泰勒级数相等的函数称为解析函数。
解析函數
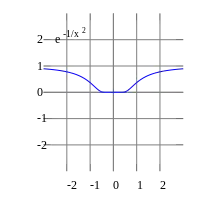
如果泰勒级数对于区间中的所有都收敛并且级数的和等于,那么我们就称函数为解析形的函数(analytic)。一个函数当且仅当(简单地说,“只有在且只要在”)能够被表示为幂级数的形式时,才是解析形的函数。通常会用泰勒定理来估计级数的餘项,这样就能够确定级数是否收敛于。上面给出的幂级数展开式中的系数正好是泰勒级数中的系数。
以下三个事实可以说明为什么泰勒级数是十分重要的:
- 可以逐项对幂级数的计算微分和积分,因此求和函数相对比较容易。
- 数学家因此能够在复数平面上研究函数,因为一个解析函数,也可以被定义为在复平面中一个开放的区间内的解析函数(在区间内每一个点上都能被微分的函数)。
- 可用泰勒级数估计,在某一点上函数会计算出什么值。
对于一些无穷的可以被微分函数,虽然它们的展开式会收敛,但是并不等于。例如,分段函数,如果并且,则时所有的导数都为零,所以这个的泰勒级数为零,且其收敛半径为无穷大,不过函数仅在处为零。但是,在以复数作为变量的函数中这个问题并不存在,因为当沿虚轴趋于零,并不趋于零。
如果一个函数在某处引发一个奇点,它就无法被展开为泰勒级数,不过如果变量是负指数幂的话,我们仍然可以将其展开为一个级数。例如,虽然在的时候,会引发奇点,但仍然能够把这个函数展开为一个洛朗级数。
最近,专家们发现了一个用泰勒级数来求解微分方程的方法——Parker-Sochacki method[1]。用皮卡反覆運算便可以推导出这个方法。
常用的函数:麦克劳林級數
下面我们给出了几个重要的麦克劳林级数。当变量是复数时,这些等式依然成立。
几何级数
由无穷递缩等比数列求和式:
二项式级数
双曲函数
- 展开式中的Bk是伯努利数。
朗伯W函数
历史
希腊哲学家芝诺在考虑了利用无穷级数求和来得到有限结果的问题,得出不可能的结论 - 芝诺悖论。后来,亚里士多德对芝诺悖论在哲学上进行了反驳,但德谟克利特以及后来的阿基米德进行研究,此部分数学内容才得到解决。 正是用了阿基米德的穷竭法才使得一个无穷级数被逐步的细分,得到了有限的结果。[2]几个世纪之后,中国数学家刘徽也独立提出了类似的方法。[3]
进入14世纪,马德哈瓦最早使用了泰勒级数以及相关的方法[4]。尽管他的数学著作没有流传下来,但后来印度数学家的著作表明他发现了一些特殊的泰勒级数,这些级数包括正弦、余弦、正切、和反正切三角函数等等。之后,喀拉拉学派在他的基础上进行了一系列的延伸与合理逼近,这些工作一直持续到16世纪。
到了17世纪,詹姆斯·格雷果里同样继续着这方面的研究并且发表了若干麦克劳林级数。但是直到1715年,布鲁克·泰勒 [5] 提出了一个通用的方法来构建适用于所有函数的此类列级数。这就是后来被人们所熟知的泰勒级数。 麦克劳林级数是泰勒级数的特例,是爱丁堡大学的科林·麦克劳林教授在18世纪发表的,并以其名字命名。
與牛頓插值公式的淵源
牛頓插值公式也叫做牛頓級數,由“牛頓前向差分方程”的項組成,得名於伊薩克·牛頓爵士,最早发表为他在1687年出版的《自然哲學的數學原理》中第三編“宇宙體系”的引理五[6],此前詹姆斯·格雷果里於1670年和牛頓於1676年已經分別獨立得出這個成果。一般稱其為連續“泰勒展開”的離散對應。
参考文献
- James S. Sochacki. . James Madison University. [2008-05-02]. (原始内容存档于2008-05-01) (英语).
- Kline, M. (1990) Mathematical Thought from Ancient to Modern Times. Oxford University Press. pp. 35-37
- 吴文俊 《中国数学史大系》第三卷 367页
- . MAT 314. Canisius College. [2006-07-09]. (原始内容存档于2006-08-06).
- Taylor, Brook, Methodus Incrementorum Directa et Inversa [Direct and Reverse Methods of Incrementation] (London, 1715), pages 21-23 (Proposition VII, Theorem 3, Corollary 2). Translated into English in D. J. Struik, A Source Book in Mathematics 1200-1800 (Cambridge, Massachusetts: Harvard University Press, 1969), pages 329-332.
- Newton, Isaac, (1687). Principia, Book III, Lemma V, Case 1