均差

均差（Divided differences）是遞歸除法過程。在数值分析中，可用於計算牛頓多項式形式的多項式插值的係數。在微积分中，均差与导数一起合称差商，是对函数在一个区间内的平均变化率的测量[1][2][3]。

均差也是一种算法，查尔斯·巴贝奇的差分机，是他在1822年发表的论文中提出的一种早期的机械计算机，在历史上意图用来计算对数表和三角函数表，它设计在其运算中使用这个算法[4]。

定義

給定n+1個數據點

(x_{0},y_{0}),\ldots ,(x_{n},y_{n})

定義前向均差為：

{\begin{aligned}{\mathopen {[}}y_{\nu }]&=y_{\nu },\quad \nu \in \{0,\ldots ,n\}\\{\mathopen {[}}y_{\nu },\ldots ,y_{\nu +j}]&={\frac {[y_{\nu +1},\ldots ,y_{\nu +j}]-[y_{\nu },\ldots ,y_{\nu +j-1}]}{x_{\nu +j}-x_{\nu }}},\quad \nu \in \{0,\ldots ,n-j\},\ j\in \{1,\ldots ,n\}\\\end{aligned}}

定義後向均差為：

{\begin{aligned}{\mathopen {[}}y_{\nu }]&=y_{\nu },\quad \nu \in \{0,\ldots ,n\}\\{\mathopen {[}}y_{\nu },\ldots ,y_{\nu -j}]&={\frac {[y_{\nu },\ldots ,y_{\nu -j+1}]-[y_{\nu -1},\ldots ,y_{\nu -j}]}{x_{\nu }-x_{\nu -j}}},\quad \nu \in \{j,\ldots ,n\},\ j\in \{1,\ldots ,n\}\\\end{aligned}}

表示法

假定數據點給出為函數 ƒ，

(x_{0},f(x_{0})),\ldots ,(x_{n},f(x_{n}))

其均差可以寫為：

{\begin{aligned}f[x_{\nu }]&=f(x_{\nu }),\qquad \nu \in \{0,\ldots ,n\}\\f[x_{\nu },\ldots ,x_{\nu +j}]&={\frac {f[x_{\nu +1},\ldots ,x_{\nu +j}]-f[x_{\nu },\ldots ,x_{\nu +j-1}]}{x_{\nu +j}-x_{\nu }}},\quad \nu \in \{0,\ldots ,n-j\},\ j\in \{1,\ldots ,n\}\end{aligned}}

對函數 ƒ 在節點 x₀, ..., x_n 上的均差還有其他表示法，如：

{\begin{matrix}{\mathopen {[}}x_{0},\ldots ,x_{n}]f\\{\mathopen {[}}x_{0},\ldots ,x_{n};f]\\{\mathopen {D}}[x_{0},\ldots ,x_{n}]f\\\end{matrix}}

例子

給定ν=0：

{\begin{aligned}{\mathopen {[}}y_{0}]&=y_{0}\\{\mathopen {[}}y_{0},y_{1}]&={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}\\{\mathopen {[}}y_{0},y_{1},y_{2}]&={\frac {{\mathopen {[}}y_{1},y_{2}]-{\mathopen {[}}y_{0},y_{1}]}{x_{2}-x_{0}}}\\{\mathopen {[}}y_{0},y_{1},y_{2},y_{3}]&={\frac {{\mathopen {[}}y_{1},y_{2},y_{3}]-{\mathopen {[}}y_{0},y_{1},y_{2}]}{x_{3}-x_{0}}}\\{\mathopen {[}}y_{0},y_{1},\dots ,y_{n}]&={\frac {{\mathopen {[}}y_{1},y_{2},\dots ,y_{n}]-{\mathopen {[}}y_{0},y_{1},\dots ,y_{n-1}]}{x_{n}-x_{0}}}\end{aligned}}

為了使涉及的遞歸過程更加清楚，以列表形式展示均差的計算過程[5]：

{\begin{matrix}x_{0}&[y_{0}]=y_{0}&&&\\&&[y_{0},y_{1}]&&\\x_{1}&[y_{1}]=y_{1}&&[y_{0},y_{1},y_{2}]&\\&&[y_{1},y_{2}]&&[y_{0},y_{1},y_{2},y_{3}]\\x_{2}&[y_{2}]=y_{2}&&[y_{1},y_{2},y_{3}]&\\&&[y_{2},y_{3}]&&\\x_{3}&[y_{3}]=y_{3}&&&\\\end{matrix}}

展開形式

用數學歸納法可證明[6]：

{\begin{aligned}{\mathopen {[}}y_{0}]&=y_{0}\\{\mathopen {[}}y_{0},y_{1}]&={\frac {y_{0}}{x_{0}-x_{1}}}+{\frac {y_{1}}{x_{1}-x_{0}}}\\{\mathopen {[}}y_{0},y_{1},y_{2}]&={\frac {y_{0}}{(x_{0}-x_{1})(x_{0}-x_{2})}}+{\frac {y_{1}}{(x_{1}-x_{0})(x_{1}-x_{2})}}+{\frac {y_{2}}{(x_{2}-x_{0})(x_{2}-x_{1})}}\\{\mathopen {[}}y_{0},y_{1},\dots ,y_{n}]&=\sum _{j=0}^{n}{\frac {y_{j}}{\prod _{k=0,\,k\neq j}^{n}(x_{j}-x_{k})}}\\\end{aligned}}

此公式體現了均差的對稱性質。[7]故可推知：任意调换數據點次序，其值不变。[8]

性质

对称性：若 ${\displaystyle \sigma$ 是一个排列则

f[x_{0},\dots ,x_{n}]=f[x_{\sigma (0)},\dots ,x_{\sigma (n)}]

線性：

{\begin{aligned}(f+g)[x_{0},\dots ,x_{n}]&=f[x_{0},\dots ,x_{n}]+g[x_{0},\dots ,x_{n}]\\(\lambda \cdot f)[x_{0},\dots ,x_{n}]&=\lambda \cdot f[x_{0},\dots ,x_{n}]\\\end{aligned}}

萊布尼茨法則：

(f\cdot g)[x_{0},\dots ,x_{n}]=f[x_{0}]\cdot g[x_{0},\dots ,x_{n}]+f[x_{0},x_{1}]\cdot g[x_{1},\dots ,x_{n}]+\dots +f[x_{0},\dots ,x_{n}]\cdot g[x_{n}]

均差中值定理：

\exists \xi \in (\min\{x_{0},\dots ,x_{n}\},\max\{x_{0},\dots ,x_{n}\})\quad f[x_{0},\dots ,x_{n}]={\frac {f^{(n)}(\xi )}{n!}}

等價定義

通過對換 n 阶均差中(x₀,y₀)与(x_n-1,y_n-1)，可得到等價定義：

{\begin{aligned}{\mathopen {[}}y_{0},y_{1},\dots ,y_{n-1},y_{n}]&={\frac {{\mathopen {[}}y_{1},y_{2},\dots ,y_{n}]-{\mathopen {[}}y_{0},y_{1},\dots ,y_{n-1}]}{x_{n}-x_{0}}}\\&={\frac {{\mathopen {[}}y_{1},\dots ,y_{n-2},y_{0},y_{n}]-{\mathopen {[}}y_{n-1},y_{1},\dots ,y_{n-2},y_{0}]}{x_{n}-x_{n-1}}}\\&={\frac {{\mathopen {[}}y_{0},\dots ,y_{n-2},y_{n}]-{\mathopen {[}}y_{0},y_{1},\dots ,y_{n-1}]}{x_{n}-x_{n-1}}}\\\end{aligned}}

這個定義有著不同的計算次序：

{\begin{aligned}{\mathopen {[}}y_{0}]&=y_{0}\\{\mathopen {[}}y_{0},y_{1}]&={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}\\{\mathopen {[}}y_{0},y_{1},y_{2}]&={\frac {{\mathopen {[}}y_{0},y_{2}]-{\mathopen {[}}y_{0},y_{1}]}{x_{2}-x_{1}}}\\{\mathopen {[}}y_{0},y_{1},y_{2},y_{3}]&={\frac {{\mathopen {[}}y_{0},y_{1},y_{3}]-{\mathopen {[}}y_{0},y_{1},y_{2}]}{x_{3}-x_{2}}}\\{\mathopen {[}}y_{0},y_{1},\dots ,y_{n}]&={\frac {{\mathopen {[}}y_{0},\dots ,y_{n-2},y_{n}]-{\mathopen {[}}y_{0},y_{1},\dots ,y_{n-1}]}{x_{n}-x_{n-1}}}\\\end{aligned}}

以列表形式展示這個定義下均差的計算過程[9]：

{\begin{matrix}x_{0}&[y_{0}]=y_{0}&&&\\&&[y_{0},y_{1}]&&\\x_{1}&[y_{1}]=y_{1}&&[y_{0},y_{1},y_{2}]&\\&&[y_{0},y_{2}]&&[y_{0},y_{1},y_{2},y_{3}]\\x_{2}&[y_{2}]=y_{2}&&[y_{0},y_{1},y_{3}]&\\&&[y_{0},y_{3}]&&\\x_{3}&[y_{3}]=y_{3}&&&\\\end{matrix}}

牛頓插值法

《自然哲學的數學原理》的第三編“宇宙體系”的引理五的图例。這裡在橫坐標上有6個點H,I,K,L,M,N，對應著6個值A,B,C,D,E,F，生成一個多項式函數對這6個點上有對應的6個值，計算任意點S對應的值R。牛頓給出了間距為單位值和任意值的兩種情況。

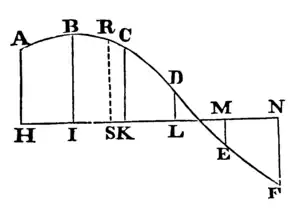
牛頓插值公式，得名於伊薩克·牛頓爵士，最早发表为他在1687年出版的《自然哲學的數學原理》中第三編“宇宙體系”的引理五，此前詹姆斯·格雷果里於1670年和牛頓於1676年已經分別獨立得出這個成果。一般稱其為連續泰勒展開的離散對應。

使用均差的牛顿插值法為[10]：

{\begin{aligned}N_{n}(x)&=y_{0}+(x-{x}_{0})\left([{y}_{0},{y}_{1}]+(x-{x}_{1})\left([{y}_{0},{y}_{1},{y}_{2}]+\cdots \right)\right)\\&=[y_{0}]+[{y}_{0},{y}_{1}](x-{x}_{0})+\cdots +[{y}_{0},{y}_{1},\ldots ,{y}_{n}]\prod _{k=0}^{n-1}(x-{x}_{k})\end{aligned}}

可以在计算过程中任意增添节点如點(x_n+1,y_n+1)，只需計算新增的n+1階均差及其插值基函數，而无拉格朗日插值法需重算全部插值基函数之虞。

對均差採用展開形式[11]：

{\begin{aligned}N_{n}(x)&=y_{0}+y_{0}{\frac {x-{x}_{0}}{x_{0}-x_{1}}}+y_{1}{\frac {x-{x}_{0}}{x_{1}-x_{0}}}+\cdots +\sum _{j=0}^{n}y_{j}{\frac {\prod _{k=0}^{n-1}(x-{x}_{k})}{\prod _{k=0,\,k\neq j}^{n}(x_{j}-x_{k})}}\\\end{aligned}}

以2階均差牛頓插值為例：

{\begin{aligned}N_{2}(x)&=y_{0}\left(1+{\frac {x-{x}_{0}}{x_{0}-x_{1}}}+{\frac {(x-x_{0})(x-x_{1})}{(x_{0}-x_{1})(x_{0}-x_{2})}}\right)+y_{1}\left({\frac {x-{x}_{0}}{x_{1}-x_{0}}}+{\frac {(x-x_{0})(x-x_{1})}{(x_{1}-x_{0})(x_{1}-x_{2})}}\right)+y_{2}{\frac {(x-x_{0})(x-x_{1})}{(x_{2}-x_{0})(x_{2}-x_{1})}}\\&=y_{0}{\frac {(x-x_{1})(x-x_{2})}{(x_{0}-x_{1})(x_{0}-x_{2})}}+y_{1}{\frac {(x-x_{0})(x-x_{2})}{(x_{1}-x_{0})(x_{1}-x_{2})}}+y_{2}{\frac {(x-x_{0})(x-x_{1})}{(x_{2}-x_{0})(x_{2}-x_{1})}}\\&=\sum _{j=0}^{2}y_{j}\prod _{\begin{smallmatrix}k=0\\k\neq j\end{smallmatrix}}^{2}{\frac {x-{x}_{k}}{x_{j}-x_{k}}}\\\end{aligned}}

前向差分

當數據點呈等距分佈的時候，這個特殊情況叫做“前向差分”。它們比計算一般的均差要容易。

定義

給定n+1個數據點

(x_{0},y_{0}),\ldots ,(x_{n},y_{n})

有著

x_{i}=x_{0}+ih,\quad h>0{\mbox{ , }}0\leq i\leq n

定義前向差分為：

{\begin{aligned}\triangle ^{0}y_{i}&=y_{i}\\\triangle ^{k}y_{i}&=\triangle ^{k-1}y_{i+1}-\triangle ^{k-1}y_{i},\quad 1\leq k\leq n-i\\\end{aligned}}

前向差分所对应的均差为[12]：

f[x_{0},x_{1},\ldots ,x_{k}]={\frac {1}{k!h^{k}}}\Delta ^{(k)}f(x_{0})

例子

{\begin{matrix}y_{0}&&&\\&\triangle y_{0}&&\\y_{1}&&\triangle ^{2}y_{0}&\\&\triangle y_{1}&&\triangle ^{3}y_{0}\\y_{2}&&\triangle ^{2}y_{1}&\\&\triangle y_{2}&&\\y_{3}&&&\\\end{matrix}}

展開形式

差分的展開形式是均差展開形式的特殊情況[13]：

{\begin{aligned}\triangle ^{k}y_{i}&=\sum _{j=0}^{k}(-1)^{k-j}{\binom {k}{j}}y_{i+j},\quad 0\leq k\leq n-i\end{aligned}}

這裡的表達式

{n \choose k}={\frac {(n)_{k}}{k!}}\quad \quad (n)_{k}=n(n-1)(n-2)\cdots (n-k+1)

是二項式係數，其中的(n)_k是“下降階乘冪”，空積(n)₀被定義為1。

插值公式

其對應的牛頓插值公式為：

{\begin{aligned}f(x)&=y_{0}+{\frac {x-x_{0}}{h}}\left(\Delta ^{1}y_{0}+{\frac {x-x_{0}-h}{2h}}\left(\Delta ^{2}y_{0}+\cdots \right)\right)\\&=y_{0}+\sum _{k=1}^{n}{\frac {\Delta ^{k}y_{0}}{k!h^{k}}}\prod _{i=0}^{n-1}(x-x_{0}-ih)\\&=y_{0}+\sum _{k=1}^{n}{\frac {\Delta ^{k}y_{0}}{k!}}\prod _{i=0}^{n-1}({\frac {x-x_{0}}{h}}-i)\\&=\sum _{k=0}^{n}{{\frac {x-x_{0}}{h}} \choose k}~\Delta ^{k}y_{0}\\\end{aligned}}

無窮級數

牛頓在1665年得出並在1671年寫的《流數法》中發表了ln(1+x)的無窮級數，在1666年得出了arcsin(x)和arctan(x)的無窮級數，在1669年的《分析學》中發表了sin(x)、cos(x)、arcsin(x)和e^x的無窮級數；萊布尼茨在1673年大概也得出了sin(x)、cos(x)和arctan(x)的無窮級數。布魯克·泰勒在1715年著作《Methodus Incrementorum Directa et Inversa》[14]中研討了“有限差分”方法，其中論述了他在1712年得出的泰勒定理，這個成果此前詹姆斯·格雷果里在1670年和萊布尼茨在1673年已經得出，而約翰·伯努利在1694年已經在《教師學報》發表。

他對牛頓的均差的步長取趨於0的極限，得出：

{\begin{aligned}f(x)&=f(a)+\lim _{h\to 0}\sum _{k=1}^{\infty }{\frac {\Delta _{h}^{k}[f](a)}{k!h^{k}}}\prod _{i=0}^{k-1}((x-a)-ih)\\&=f(a)+\sum _{k=1}^{\infty }{\frac {d^{k}}{dx^{k}}}f(a){\frac {(x-a)^{k}}{k!}}\\\end{aligned}}

冪函數的均差

使用普通函數記號表示冪运算， $p_{n}(x)=x^{n}$ ，有：

{\begin{aligned}p_{j}[x_{0},\dots ,x_{n}]&=0\qquad \forall j<n\\p_{n}[x_{0},\dots ,x_{n}]&=1\\p_{n+1}[x_{0},\dots ,x_{n}]&=x_{0}+\dots +x_{n}\\p_{n+m}[x_{0},\dots ,x_{n}]&=\sum _{k_{0}+\cdots +k_{n}=m}{\begin{matrix}\prod _{t=0}^{n}x_{t}^{k_{t}}\end{matrix}}\\\end{aligned}}

此中n+1元m次齊次多項式的記法同於多項式定理。

泰勒形式

泰勒級數和任何其他的函數級數，在原理上都可以用來逼近均差。將泰勒級數表示為:

f=f(0)p_{0}+f'(0)p_{1}+{\frac {f''(0)}{2!}}p_{2}+\dots

均差的泰勒級數為：

f[x_{0},\dots ,x_{n}]=f(0)p_{0}[x_{0},\dots ,x_{n}]+f'(0)p_{1}[x_{0},\dots ,x_{n}]+\dots +{\frac {f^{(n)}(0)}{n!}}p_{n}[x_{0},\dots ,x_{n}]+\dots

前 $n$ 項消失了，因為均差的階高於多項式的階。可以得出均差的泰勒級數本質上開始於：

{\frac {f^{(n)}(0)}{n!}}

依據均差中值定理，這也是均差的最簡單逼近。

皮亞諾形式

均差還可以表達為

f[x_{0},\ldots ,x_{n}]={\frac {1}{n!}}\int _{x_{0}}^{x_{n}}f^{(n)}(t)B_{n-1}(t)\,dt

這裡的B_n-1是數據點x₀,...,x_n的n-1次B樣條，而f⁽ⁿ⁾是函數f的n階導數。這叫做均差的皮亞諾形式，而B_n-1是均差的皮亞諾核。

註釋與引用

Frank C. Wilson; Scott Adamson. . Cengage Learning. 2008: 177. ISBN 0-618-61104-5.
Tamara Lefcourt Ruby; James Sellers; Lisa Korf; Jeremy Van Horn; Mike Munn. . Kaplan Publishing. 2014: 237. ISBN 978-1-61865-686-5.
Thomas Hungerford; Douglas Shaw. . Cengage Learning. 2008: 211–212. ISBN 0-495-10833-2.
Isaacson, Walter. . Simon & Schuster. 2014: 20. ISBN 978-1-4767-0869-0.
${\begin{array}{lcl}{\begin{matrix}x_{0}&x_{0}^{2}&&\\&&x_{0}+x_{1}&&\\x_{1}&x_{1}^{2}&&1&\\&&x_{1}+x_{2}&&0\\x_{2}&x_{2}^{2}&&1&\\&&x_{2}+x_{3}&&&\\x_{3}&x_{3}^{2}&&&\\\end{matrix}}\\\\{\begin{matrix}x_{0}&x_{0}^{n}&\\&&\sum _{i=0}^{n-1}x_{0}^{n-1-i}x_{1}^{i}\\x_{1}&x_{1}^{n}&\\\end{matrix}}\\\\{\begin{matrix}x_{0}&x_{0}^{n+1}&\\&&{\frac {x_{1}^{n+1}-x_{1}x_{0}^{n}+x_{1}x_{0}^{n}-x_{0}^{n+1}}{x_{1}-x_{0}}}=x_{1}{\frac {x_{1}^{n}-x_{0}^{n}}{x_{1}-x_{0}}}+x_{0}^{n}=x_{1}\sum _{i=0}^{n-1}x_{0}^{n-1-i}x_{1}^{i}+x_{0}^{n}=\sum _{i=0}^{n}x_{0}^{n-i}x_{1}^{i}\\x_{1}&x_{1}^{n+1}&\\\end{matrix}}\\\\{\begin{matrix}x_{0}&x_{0}^{n+1}&&\\&&\sum _{i=0}^{n}x_{0}^{n-i}x_{1}^{i}&\\x_{1}&x_{1}^{n+1}&&{\frac {\sum _{i=0}^{n}x_{1}^{n-i}x_{2}^{i}-\sum _{i=0}^{n}x_{0}^{n-i}x_{1}^{i}}{x_{2}-x_{0}}}={\frac {\sum _{i=0}^{n-1}x_{1}^{i}(x_{2}^{n-i}-x_{0}^{n-i})}{x_{2}-x_{0}}}=\sum _{i+j+k=n-1}{x_{0}^{i}x_{1}^{j}x_{2}^{k}}\\&&\sum _{i=0}^{n}x_{1}^{n-i}x_{2}^{i}&\\x_{2}&x_{2}^{n+1}&&\\\end{matrix}}\\\\{\begin{matrix}x_{0}&x_{0}^{n+1}&&&\\&&\sum _{i=0}^{n}x_{0}^{n-i}x_{1}^{i}&&\\x_{1}&x_{1}^{n+1}&&\sum _{i+j+k=n-1}{x_{0}^{i}x_{1}^{j}x_{2}^{k}}&\\&&\sum _{i=0}^{n}x_{1}^{n-i}x_{2}^{i}&&{\frac {\sum _{i+j+k=n-1}{x_{1}^{i}x_{2}^{j}x_{3}^{k}}-\sum _{i+j+k=n-1}{x_{0}^{i}x_{1}^{j}x_{2}^{k}}}{x_{3}-x_{0}}}=\sum _{i+j+k+l=n-2}{x_{0}^{i}x_{1}^{j}x_{2}^{k}x_{3}^{l}}\\x_{2}&x_{2}^{n+1}&&\sum _{i+j+k=n-1}{x_{1}^{i}x_{2}^{j}x_{3}^{k}}&\\&&\sum _{i=0}^{n}x_{2}^{n-i}x_{3}^{i}&&\\x_{3}&x_{3}^{n+1}&&&\\\end{matrix}}\\\\{\begin{matrix}x_{0}&x_{0}^{3}&&&&\\&&x_{0}^{2}+x_{0}x_{1}+x_{1}^{2}&&\\x_{1}&x_{1}^{3}&&x_{0}+x_{1}+x_{2}&&\\&&x_{1}^{1}+x_{1}x_{2}+x_{2}^{2}&&1&\\x_{2}&x_{2}^{3}&&x_{1}+x_{2}+x_{3}&&0\\&&x_{2}^{2}+x_{2}x_{3}+x_{3}^{2}&&1&\\x_{3}&x_{3}^{3}&&x_{2}+x_{3}+x_{4}&&\\&&x_{3}^{2}+x_{3}x_{4}+x_{4}^{2}&&&\\x_{4}&x_{4}^{3}&&&&\\\end{matrix}}\\\\{\begin{matrix}x_{0}&x_{0}^{4}&&&&&\\&&x_{0}^{3}+x_{0}^{2}x_{1}+x_{0}x_{1}^{2}+x_{1}^{3}&&&\\x_{1}&x_{1}^{4}&&x_{0}^{2}+x_{0}x_{1}+x_{1}^{2}+x_{0}x_{2}+x_{1}x_{2}+x_{2}^{2}&&&\\&&x_{1}^{3}+x_{1}^{2}x_{2}+x_{1}x_{2}^{2}+x_{2}^{3}&&x_{0}+x_{1}+x_{2}+x_{3}&\\x_{2}&x_{2}^{4}&&x_{1}^{2}+x_{1}x_{2}+x_{2}^{2}+x_{1}x_{3}+x_{2}x_{3}+x_{3}^{2}&&1&\\&&x_{2}^{3}+x_{2}^{2}x_{3}+x_{2}x_{3}^{2}+x_{3}^{3}&&x_{1}+x_{2}+x_{3}+x_{4}&&0\\x_{3}&x_{3}^{4}&&x_{2}^{2}+x_{2}x_{3}+x_{3}^{2}+x_{2}x_{4}+x_{3}x_{4}+x_{4}^{2}&&1&\\&&x_{3}^{3}+x_{3}^{2}x_{4}+x_{3}x_{4}^{2}+x_{4}^{3}&&x_{2}+x_{3}+x_{4}+x_{5}&&\\x_{4}&x_{4}^{4}&&x_{3}^{2}+x_{3}x_{4}+x_{4}^{2}+x_{3}x_{5}+x_{4}x_{5}+x_{5}^{2}&&&\\&&x_{4}^{3}+x_{4}^{2}x_{5}+x_{4}x_{5}^{2}+x_{5}^{3}&&&&\\x_{5}&x_{5}^{4}&&&&&\\\end{matrix}}\\\\{\begin{matrix}x_{0}&x_{0}^{5}&&&&&&\\&&\sum _{i=0}^{4}x_{0}^{4-i}x_{1}^{i}&&&&\\x_{1}&x_{1}^{5}&&\sum _{i+j+k=3}x_{0}^{i}x_{1}^{j}x_{2}^{k}&&&&\\&&\sum _{i=0}^{4}x_{1}^{4-i}x_{2}^{i}&&\sum _{i+j+k+l=2}x_{0}^{i}x_{1}^{j}x_{2}^{k}x_{3}^{l}&&&\\x_{2}&x_{2}^{5}&&\sum _{i+j+k=3}x_{1}^{i}x_{2}^{j}x_{3}^{k}&&\sum _{i=0}^{4}x_{i}&&\\&&\sum _{i=0}^{4}x_{2}^{4-i}x_{3}^{i}&&\sum _{i+j+k+l=2}x_{1}^{i}x_{2}^{j}x_{3}^{k}x_{4}^{l}&&1&\\x_{3}&x_{3}^{5}&&\sum _{i+j+k=3}x_{2}^{i}x_{3}^{j}x_{4}^{k}&&\sum _{i=1}^{5}x_{i}&&0\\&&\sum _{i=0}^{4}x_{3}^{4-i}x_{4}^{i}&&\sum _{i+j+k+l=2}x_{2}^{i}x_{3}^{j}x_{4}^{j}x_{5}^{l}&&1&\\x_{4}&x_{4}^{5}&&\sum _{i+j+k=3}x_{3}^{i}x_{4}^{j}x_{5}^{k}&&\sum _{i=2}^{6}x_{i}&&\\&&\sum _{i=0}^{4}x_{4}^{4-i}x_{5}^{i}&&\sum _{i+j+k+l=2}x_{3}^{i}x_{4}^{j}x_{5}^{k}x_{6}^{l}&&&\\x_{5}&x_{5}^{5}&&\sum _{i+j+k=3}x_{4}^{i}x_{5}^{j}x_{6}^{k}&&&&\\&&\sum _{i=0}^{4}x_{5}^{4-i}x_{6}^{i}&&&&&\\x_{6}&x_{6}^{5}&&&&&&\\\end{matrix}}\\\end{array}}$
${\begin{aligned}{\mathopen {[}}y_{0}]&=y_{0}\\{\mathopen {[}}y_{0},y_{1}]&={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}={\frac {y_{0}}{x_{0}-x_{1}}}+{\frac {y_{1}}{x_{1}-x_{0}}}\\&=\sum _{j=0}^{1}{\frac {y_{j}}{\prod _{k=0,k\neq j}^{1}(x_{j}-x_{k})}}\\{\mathopen {[}}y_{0},y_{1},y_{2}]&={\frac {{\cfrac {y_{1}}{x_{1}-x_{2}}}+{\cfrac {y_{2}}{x_{2}-x_{1}}}-{\cfrac {y_{0}}{x_{0}-x_{1}}}-{\cfrac {y_{1}}{x_{1}-x_{0}}}}{x_{2}-x_{0}}}\\&={\frac {y_{0}}{(x_{0}-x_{1})(x_{0}-x_{2})}}+{\frac {y_{1}}{(x_{1}-x_{0})(x_{1}-x_{2})}}+{\frac {y_{2}}{(x_{2}-x_{0})(x_{2}-x_{1})}}\\&=\sum _{j=0}^{2}{\frac {y_{j}}{\prod _{k=0,k\neq j}^{2}(x_{j}-x_{k})}}\\{\mathopen {[}}y_{0},y_{1},\dots ,y_{n}]&=\sum _{j=0}^{n}{\frac {y_{j}}{\prod _{k=0,k\neq j}^{n}(x_{j}-x_{k})}}\\{\mathopen {[}}y_{0},y_{1},\dots ,y_{n+1}]&={\frac {\sum _{j=1}^{n+1}{\frac {y_{j}}{\prod _{k=1,\,k\neq j}^{n+1}(x_{j}-x_{k})}}-\sum _{j=0}^{n}{\frac {y_{j}}{\prod _{k=0,\,k\neq j}^{n}(x_{j}-x_{k})}}}{x_{n+1}-x_{0}}}\\&={\frac {{\frac {y_{n+1}}{\prod _{k=1}^{n}(x_{n+1}-x_{k})}}+\sum _{j=1}^{n}y_{j}\left({\frac {1}{\prod _{k=1,\,k\neq j}^{n+1}(x_{j}-x_{k})}}-{\frac {1}{\prod _{k=0,\,k\neq j}^{n}(x_{j}-x_{k})}}\right)-{\frac {y_{0}}{\prod _{k=1}^{n}(x_{0}-x_{k})}}}{x_{n+1}-x_{0}}}\\&={\frac {{\frac {y_{n+1}}{\prod _{k=1}^{n}(x_{n+1}-x_{k})}}+\sum _{j=1}^{n}y_{j}\left({\frac {x_{j}-x_{0}}{\prod _{k=0,\,k\neq j}^{n+1}(x_{j}-x_{k})}}-{\frac {x_{j}-x_{n+1}}{\prod _{k=0,\,k\neq j}^{n+1}(x_{j}-x_{k})}}\right)-{\frac {y_{0}}{\prod _{k=1}^{n}(x_{0}-x_{k})}}}{x_{n+1}-x_{0}}}\\&={\frac {{\frac {y_{n+1}}{\prod _{k=1}^{n}(x_{n+1}-x_{k})}}+\sum _{j=1}^{n}y_{j}\left({\frac {x_{n+1}-x_{0}}{\prod _{k=0,\,k\neq j}^{n+1}(x_{j}-x_{k})}}\right)-{\frac {y_{0}}{\prod _{k=1}^{n}(x_{0}-x_{k})}}}{x_{n+1}-x_{0}}}\\&={\frac {y_{n+1}}{\prod _{k=0}^{n}(x_{n+1}-x_{k})}}+\sum _{j=1}^{n}{\frac {y_{j}}{\prod _{k=0,\,k\neq j}^{n+1}(x_{j}-x_{k})}}+{\frac {y_{0}}{\prod _{k=1}^{n+1}(x_{0}-x_{k})}}\\&=\sum _{j=0}^{n+1}{\frac {y_{j}}{\prod _{k=0,\,k\neq j}^{n+1}(x_{j}-x_{k})}}\end{aligned}}$
《数值分析及科学计算》薛毅（编）第六章第2节 Newton插值. P200.
《数值分析及科学计算》薛毅（编）第六章第2节 Newton插值. P201.
${\begin{matrix}x_{0}&x_{0}^{3}&&&&\\&&x_{0}^{2}+x_{0}x_{1}+x_{1}^{2}&&\\x_{1}&x_{1}^{3}&&x_{0}+x_{1}+x_{2}&&\\&&x_{0}^{2}+x_{0}x_{2}+x_{2}^{2}&&1&\\x_{2}&x_{2}^{3}&&x_{0}+x_{1}+x_{3}&&0\\&&x_{0}^{2}+x_{0}x_{3}+x_{3}^{2}&&1&\\x_{3}&x_{3}^{3}&&x_{0}+x_{1}+x_{4}&&\\&&x_{0}^{2}+x_{0}x_{4}+x_{4}^{2}&&&\\x_{4}&x_{4}^{3}&&&&\\\end{matrix}}$
. [2019-04-19]. （原始内容存档于2019-04-19）.
${\begin{array}{lcl}{\begin{aligned}N_{1}(x)&=[y_{0}]+[{y}_{0},{y}_{1}](x-{x}_{0})=y_{0}+y_{0}{\frac {x-{x}_{0}}{x_{0}-x_{1}}}+y_{1}{\frac {x-{x}_{0}}{x_{1}-x_{0}}}=y_{0}(1+{\frac {x-{x}_{0}}{x_{0}-x_{1}}})+y_{1}{\frac {x-{x}_{0}}{x_{1}-x_{0}}}\\&=y_{0}{\frac {x-{x}_{1}}{x_{0}-x_{1}}}+y_{1}{\frac {x-{x}_{0}}{x_{1}-x_{0}}}=\sum _{j=0}^{1}y_{j}\prod _{k=0,k\neq j}^{1}{\frac {x-{x}_{k}}{x_{j}-x_{k}}}\\\end{aligned}}\\{\begin{aligned}N_{n}(x)&=\sum _{j=0}^{n}y_{j}\prod _{k=0,k\neq j}^{n}{\frac {x-{x}_{k}}{x_{j}-x_{k}}}\\\end{aligned}}\\{\begin{aligned}N_{n+1}(x)&=N_{n}(x)+[{y}_{0},{y}_{1},\ldots ,{y}_{n+1}]\prod _{k=0}^{n}(x-{x}_{k})\\&=\sum _{j=0}^{n}y_{j}\prod _{k=0,k\neq j}^{n}{\frac {x-{x}_{k}}{x_{j}-x_{k}}}+\sum _{j=0}^{n+1}y_{j}{\frac {\prod _{k=0}^{n}(x-{x}_{k})}{\prod _{k=0,\,k\neq j}^{n+1}(x_{j}-x_{k})}}\\&=\sum _{j=0}^{n}y_{j}\left({\frac {\prod _{k=0,k\neq j}^{n}(x-{x}_{k})}{\prod _{k=0,k\neq j}^{n}(x_{j}-x_{k})}}+{\frac {\prod _{k=0}^{n}(x-{x}_{k})}{\prod _{k=0,\,k\neq j}^{n+1}(x_{j}-x_{k})}}\right)+y_{n+1}{\frac {\prod _{k=0}^{n}(x-{x}_{k})}{\prod _{k=0}^{n}(x_{n+1}-x_{k})}}\\&=\sum _{j=0}^{n}y_{j}\left({\frac {\left(\prod _{k=0,k\neq j}^{n}(x-{x}_{k})\right)(x_{j}-x_{n+1})}{\prod _{k=0,k\neq j}^{n+1}(x_{j}-x_{k})}}+{\frac {\left(\prod _{k=0,k\neq j}^{n}(x-{x}_{k})\right)(x-x_{j})}{\prod _{k=0,\,k\neq j}^{n+1}(x_{j}-x_{k})}}\right)+y_{n+1}{\frac {\prod _{k=0}^{n}(x-{x}_{k})}{\prod _{k=0}^{n}(x_{n+1}-x_{k})}}\\&=\sum _{j=0}^{n}y_{j}{\frac {\left(\prod _{k=0,k\neq j}^{n}(x-{x}_{k})\right)(x-x_{n+1})}{\prod _{k=0,k\neq j}^{n+1}(x_{j}-x_{k})}}+y_{n+1}{\frac {\prod _{k=0}^{n}(x-{x}_{k})}{\prod _{k=0}^{n}(x_{n+1}-x_{k})}}\\&=\sum _{j=0}^{n+1}y_{j}\prod _{k=0,k\neq j}^{n+1}{\frac {x-{x}_{k}}{x_{j}-x_{k}}}\\\end{aligned}}\\\end{array}}$
Burden, Richard L.; Faires, J. Douglas. 9th. 2011: 129.
${\begin{aligned}\triangle ^{k}y_{i}&=\sum _{j=0}^{k}{\frac {k!}{\prod _{l=0,\,l\neq j}^{k}(j-l)}}y_{i+j},\quad 0\leq k\leq n-i\\&=\sum _{j=0}^{k}{\frac {k!}{j!(-1)^{k-j}(k-j)!}}y_{i+j},\quad 0\leq k\leq n-i\\&=\sum _{j=0}^{k}(-1)^{k-j}{\binom {k}{j}}y_{i+j},\quad 0\leq k\leq n-i\end{aligned}}$
Methodus Incrementorum Directa et Inversa（页面存档备份，存于）

参考书目

Louis Melville Milne-Thomson. . American Mathematical Soc. 2000. Chapter 1: Divided Differences [1933]. ISBN 978-0-8218-2107-7.
Myron B. Allen; Eli L. Isaacson. . John Wiley & Sons. 1998. Appendix A. ISBN 978-1-118-03027-1.
Ron Goldman. . Morgan Kaufmann. 2002. Chapter 4:Newton Interpolation and Difference Triangles. ISBN 978-0-08-051547-2.

參見

差分
差商
插值
牛頓多項式

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[WilsonAdamson2008-1] Frank C. Wilson; Scott Adamson. . Cengage Learning. 2008: 177. ISBN 0-618-61104-5.

[RubySellers2014-2] Tamara Lefcourt Ruby; James Sellers; Lisa Korf; Jeremy Van Horn; Mike Munn. . Kaplan Publishing. 2014: 237. ISBN 978-1-61865-686-5.

[HungerfordShaw2008-3] Thomas Hungerford; Douglas Shaw. . Cengage Learning. 2008: 211–212. ISBN 0-495-10833-2.

[Isaacson2014-4] Isaacson, Walter. . Simon & Schuster. 2014: 20. ISBN 978-1-4767-0869-0.

[5] ${\begin{array}{lcl}{\begin{matrix}x_{0}&x_{0}^{2}&&\\&&x_{0}+x_{1}&&\\x_{1}&x_{1}^{2}&&1&\\&&x_{1}+x_{2}&&0\\x_{2}&x_{2}^{2}&&1&\\&&x_{2}+x_{3}&&&\\x_{3}&x_{3}^{2}&&&\\\end{matrix}}\\\\{\begin{matrix}x_{0}&x_{0}^{n}&\\&&\sum _{i=0}^{n-1}x_{0}^{n-1-i}x_{1}^{i}\\x_{1}&x_{1}^{n}&\\\end{matrix}}\\\\{\begin{matrix}x_{0}&x_{0}^{n+1}&\\&&{\frac {x_{1}^{n+1}-x_{1}x_{0}^{n}+x_{1}x_{0}^{n}-x_{0}^{n+1}}{x_{1}-x_{0}}}=x_{1}{\frac {x_{1}^{n}-x_{0}^{n}}{x_{1}-x_{0}}}+x_{0}^{n}=x_{1}\sum _{i=0}^{n-1}x_{0}^{n-1-i}x_{1}^{i}+x_{0}^{n}=\sum _{i=0}^{n}x_{0}^{n-i}x_{1}^{i}\\x_{1}&x_{1}^{n+1}&\\\end{matrix}}\\\\{\begin{matrix}x_{0}&x_{0}^{n+1}&&\\&&\sum _{i=0}^{n}x_{0}^{n-i}x_{1}^{i}&\\x_{1}&x_{1}^{n+1}&&{\frac {\sum _{i=0}^{n}x_{1}^{n-i}x_{2}^{i}-\sum _{i=0}^{n}x_{0}^{n-i}x_{1}^{i}}{x_{2}-x_{0}}}={\frac {\sum _{i=0}^{n-1}x_{1}^{i}(x_{2}^{n-i}-x_{0}^{n-i})}{x_{2}-x_{0}}}=\sum _{i+j+k=n-1}{x_{0}^{i}x_{1}^{j}x_{2}^{k}}\\&&\sum _{i=0}^{n}x_{1}^{n-i}x_{2}^{i}&\\x_{2}&x_{2}^{n+1}&&\\\end{matrix}}\\\\{\begin{matrix}x_{0}&x_{0}^{n+1}&&&\\&&\sum _{i=0}^{n}x_{0}^{n-i}x_{1}^{i}&&\\x_{1}&x_{1}^{n+1}&&\sum _{i+j+k=n-1}{x_{0}^{i}x_{1}^{j}x_{2}^{k}}&\\&&\sum _{i=0}^{n}x_{1}^{n-i}x_{2}^{i}&&{\frac {\sum _{i+j+k=n-1}{x_{1}^{i}x_{2}^{j}x_{3}^{k}}-\sum _{i+j+k=n-1}{x_{0}^{i}x_{1}^{j}x_{2}^{k}}}{x_{3}-x_{0}}}=\sum _{i+j+k+l=n-2}{x_{0}^{i}x_{1}^{j}x_{2}^{k}x_{3}^{l}}\\x_{2}&x_{2}^{n+1}&&\sum _{i+j+k=n-1}{x_{1}^{i}x_{2}^{j}x_{3}^{k}}&\\&&\sum _{i=0}^{n}x_{2}^{n-i}x_{3}^{i}&&\\x_{3}&x_{3}^{n+1}&&&\\\end{matrix}}\\\\{\begin{matrix}x_{0}&x_{0}^{3}&&&&\\&&x_{0}^{2}+x_{0}x_{1}+x_{1}^{2}&&\\x_{1}&x_{1}^{3}&&x_{0}+x_{1}+x_{2}&&\\&&x_{1}^{1}+x_{1}x_{2}+x_{2}^{2}&&1&\\x_{2}&x_{2}^{3}&&x_{1}+x_{2}+x_{3}&&0\\&&x_{2}^{2}+x_{2}x_{3}+x_{3}^{2}&&1&\\x_{3}&x_{3}^{3}&&x_{2}+x_{3}+x_{4}&&\\&&x_{3}^{2}+x_{3}x_{4}+x_{4}^{2}&&&\\x_{4}&x_{4}^{3}&&&&\\\end{matrix}}\\\\{\begin{matrix}x_{0}&x_{0}^{4}&&&&&\\&&x_{0}^{3}+x_{0}^{2}x_{1}+x_{0}x_{1}^{2}+x_{1}^{3}&&&\\x_{1}&x_{1}^{4}&&x_{0}^{2}+x_{0}x_{1}+x_{1}^{2}+x_{0}x_{2}+x_{1}x_{2}+x_{2}^{2}&&&\\&&x_{1}^{3}+x_{1}^{2}x_{2}+x_{1}x_{2}^{2}+x_{2}^{3}&&x_{0}+x_{1}+x_{2}+x_{3}&\\x_{2}&x_{2}^{4}&&x_{1}^{2}+x_{1}x_{2}+x_{2}^{2}+x_{1}x_{3}+x_{2}x_{3}+x_{3}^{2}&&1&\\&&x_{2}^{3}+x_{2}^{2}x_{3}+x_{2}x_{3}^{2}+x_{3}^{3}&&x_{1}+x_{2}+x_{3}+x_{4}&&0\\x_{3}&x_{3}^{4}&&x_{2}^{2}+x_{2}x_{3}+x_{3}^{2}+x_{2}x_{4}+x_{3}x_{4}+x_{4}^{2}&&1&\\&&x_{3}^{3}+x_{3}^{2}x_{4}+x_{3}x_{4}^{2}+x_{4}^{3}&&x_{2}+x_{3}+x_{4}+x_{5}&&\\x_{4}&x_{4}^{4}&&x_{3}^{2}+x_{3}x_{4}+x_{4}^{2}+x_{3}x_{5}+x_{4}x_{5}+x_{5}^{2}&&&\\&&x_{4}^{3}+x_{4}^{2}x_{5}+x_{4}x_{5}^{2}+x_{5}^{3}&&&&\\x_{5}&x_{5}^{4}&&&&&\\\end{matrix}}\\\\{\begin{matrix}x_{0}&x_{0}^{5}&&&&&&\\&&\sum _{i=0}^{4}x_{0}^{4-i}x_{1}^{i}&&&&\\x_{1}&x_{1}^{5}&&\sum _{i+j+k=3}x_{0}^{i}x_{1}^{j}x_{2}^{k}&&&&\\&&\sum _{i=0}^{4}x_{1}^{4-i}x_{2}^{i}&&\sum _{i+j+k+l=2}x_{0}^{i}x_{1}^{j}x_{2}^{k}x_{3}^{l}&&&\\x_{2}&x_{2}^{5}&&\sum _{i+j+k=3}x_{1}^{i}x_{2}^{j}x_{3}^{k}&&\sum _{i=0}^{4}x_{i}&&\\&&\sum _{i=0}^{4}x_{2}^{4-i}x_{3}^{i}&&\sum _{i+j+k+l=2}x_{1}^{i}x_{2}^{j}x_{3}^{k}x_{4}^{l}&&1&\\x_{3}&x_{3}^{5}&&\sum _{i+j+k=3}x_{2}^{i}x_{3}^{j}x_{4}^{k}&&\sum _{i=1}^{5}x_{i}&&0\\&&\sum _{i=0}^{4}x_{3}^{4-i}x_{4}^{i}&&\sum _{i+j+k+l=2}x_{2}^{i}x_{3}^{j}x_{4}^{j}x_{5}^{l}&&1&\\x_{4}&x_{4}^{5}&&\sum _{i+j+k=3}x_{3}^{i}x_{4}^{j}x_{5}^{k}&&\sum _{i=2}^{6}x_{i}&&\\&&\sum _{i=0}^{4}x_{4}^{4-i}x_{5}^{i}&&\sum _{i+j+k+l=2}x_{3}^{i}x_{4}^{j}x_{5}^{k}x_{6}^{l}&&&\\x_{5}&x_{5}^{5}&&\sum _{i+j+k=3}x_{4}^{i}x_{5}^{j}x_{6}^{k}&&&&\\&&\sum _{i=0}^{4}x_{5}^{4-i}x_{6}^{i}&&&&&\\x_{6}&x_{6}^{5}&&&&&&\\\end{matrix}}\\\end{array}}$

[6] ${\begin{aligned}{\mathopen {[}}y_{0}]&=y_{0}\\{\mathopen {[}}y_{0},y_{1}]&={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}={\frac {y_{0}}{x_{0}-x_{1}}}+{\frac {y_{1}}{x_{1}-x_{0}}}\\&=\sum _{j=0}^{1}{\frac {y_{j}}{\prod _{k=0,k\neq j}^{1}(x_{j}-x_{k})}}\\{\mathopen {[}}y_{0},y_{1},y_{2}]&={\frac {{\cfrac {y_{1}}{x_{1}-x_{2}}}+{\cfrac {y_{2}}{x_{2}-x_{1}}}-{\cfrac {y_{0}}{x_{0}-x_{1}}}-{\cfrac {y_{1}}{x_{1}-x_{0}}}}{x_{2}-x_{0}}}\\&={\frac {y_{0}}{(x_{0}-x_{1})(x_{0}-x_{2})}}+{\frac {y_{1}}{(x_{1}-x_{0})(x_{1}-x_{2})}}+{\frac {y_{2}}{(x_{2}-x_{0})(x_{2}-x_{1})}}\\&=\sum _{j=0}^{2}{\frac {y_{j}}{\prod _{k=0,k\neq j}^{2}(x_{j}-x_{k})}}\\{\mathopen {[}}y_{0},y_{1},\dots ,y_{n}]&=\sum _{j=0}^{n}{\frac {y_{j}}{\prod _{k=0,k\neq j}^{n}(x_{j}-x_{k})}}\\{\mathopen {[}}y_{0},y_{1},\dots ,y_{n+1}]&={\frac {\sum _{j=1}^{n+1}{\frac {y_{j}}{\prod _{k=1,\,k\neq j}^{n+1}(x_{j}-x_{k})}}-\sum _{j=0}^{n}{\frac {y_{j}}{\prod _{k=0,\,k\neq j}^{n}(x_{j}-x_{k})}}}{x_{n+1}-x_{0}}}\\&={\frac {{\frac {y_{n+1}}{\prod _{k=1}^{n}(x_{n+1}-x_{k})}}+\sum _{j=1}^{n}y_{j}\left({\frac {1}{\prod _{k=1,\,k\neq j}^{n+1}(x_{j}-x_{k})}}-{\frac {1}{\prod _{k=0,\,k\neq j}^{n}(x_{j}-x_{k})}}\right)-{\frac {y_{0}}{\prod _{k=1}^{n}(x_{0}-x_{k})}}}{x_{n+1}-x_{0}}}\\&={\frac {{\frac {y_{n+1}}{\prod _{k=1}^{n}(x_{n+1}-x_{k})}}+\sum _{j=1}^{n}y_{j}\left({\frac {x_{j}-x_{0}}{\prod _{k=0,\,k\neq j}^{n+1}(x_{j}-x_{k})}}-{\frac {x_{j}-x_{n+1}}{\prod _{k=0,\,k\neq j}^{n+1}(x_{j}-x_{k})}}\right)-{\frac {y_{0}}{\prod _{k=1}^{n}(x_{0}-x_{k})}}}{x_{n+1}-x_{0}}}\\&={\frac {{\frac {y_{n+1}}{\prod _{k=1}^{n}(x_{n+1}-x_{k})}}+\sum _{j=1}^{n}y_{j}\left({\frac {x_{n+1}-x_{0}}{\prod _{k=0,\,k\neq j}^{n+1}(x_{j}-x_{k})}}\right)-{\frac {y_{0}}{\prod _{k=1}^{n}(x_{0}-x_{k})}}}{x_{n+1}-x_{0}}}\\&={\frac {y_{n+1}}{\prod _{k=0}^{n}(x_{n+1}-x_{k})}}+\sum _{j=1}^{n}{\frac {y_{j}}{\prod _{k=0,\,k\neq j}^{n+1}(x_{j}-x_{k})}}+{\frac {y_{0}}{\prod _{k=1}^{n+1}(x_{0}-x_{k})}}\\&=\sum _{j=0}^{n+1}{\frac {y_{j}}{\prod _{k=0,\,k\neq j}^{n+1}(x_{j}-x_{k})}}\end{aligned}}$

[7] 《数值分析及科学计算》薛毅（编）第六章第2节 Newton插值. P200.

[8] 《数值分析及科学计算》薛毅（编）第六章第2节 Newton插值. P201.

[9] ${\begin{matrix}x_{0}&x_{0}^{3}&&&&\\&&x_{0}^{2}+x_{0}x_{1}+x_{1}^{2}&&\\x_{1}&x_{1}^{3}&&x_{0}+x_{1}+x_{2}&&\\&&x_{0}^{2}+x_{0}x_{2}+x_{2}^{2}&&1&\\x_{2}&x_{2}^{3}&&x_{0}+x_{1}+x_{3}&&0\\&&x_{0}^{2}+x_{0}x_{3}+x_{3}^{2}&&1&\\x_{3}&x_{3}^{3}&&x_{0}+x_{1}+x_{4}&&\\&&x_{0}^{2}+x_{0}x_{4}+x_{4}^{2}&&&\\x_{4}&x_{4}^{3}&&&&\\\end{matrix}}$

[10] . [2019-04-19]. （原始内容存档于2019-04-19）.

[11] ${\begin{array}{lcl}{\begin{aligned}N_{1}(x)&=[y_{0}]+[{y}_{0},{y}_{1}](x-{x}_{0})=y_{0}+y_{0}{\frac {x-{x}_{0}}{x_{0}-x_{1}}}+y_{1}{\frac {x-{x}_{0}}{x_{1}-x_{0}}}=y_{0}(1+{\frac {x-{x}_{0}}{x_{0}-x_{1}}})+y_{1}{\frac {x-{x}_{0}}{x_{1}-x_{0}}}\\&=y_{0}{\frac {x-{x}_{1}}{x_{0}-x_{1}}}+y_{1}{\frac {x-{x}_{0}}{x_{1}-x_{0}}}=\sum _{j=0}^{1}y_{j}\prod _{k=0,k\neq j}^{1}{\frac {x-{x}_{k}}{x_{j}-x_{k}}}\\\end{aligned}}\\{\begin{aligned}N_{n}(x)&=\sum _{j=0}^{n}y_{j}\prod _{k=0,k\neq j}^{n}{\frac {x-{x}_{k}}{x_{j}-x_{k}}}\\\end{aligned}}\\{\begin{aligned}N_{n+1}(x)&=N_{n}(x)+[{y}_{0},{y}_{1},\ldots ,{y}_{n+1}]\prod _{k=0}^{n}(x-{x}_{k})\\&=\sum _{j=0}^{n}y_{j}\prod _{k=0,k\neq j}^{n}{\frac {x-{x}_{k}}{x_{j}-x_{k}}}+\sum _{j=0}^{n+1}y_{j}{\frac {\prod _{k=0}^{n}(x-{x}_{k})}{\prod _{k=0,\,k\neq j}^{n+1}(x_{j}-x_{k})}}\\&=\sum _{j=0}^{n}y_{j}\left({\frac {\prod _{k=0,k\neq j}^{n}(x-{x}_{k})}{\prod _{k=0,k\neq j}^{n}(x_{j}-x_{k})}}+{\frac {\prod _{k=0}^{n}(x-{x}_{k})}{\prod _{k=0,\,k\neq j}^{n+1}(x_{j}-x_{k})}}\right)+y_{n+1}{\frac {\prod _{k=0}^{n}(x-{x}_{k})}{\prod _{k=0}^{n}(x_{n+1}-x_{k})}}\\&=\sum _{j=0}^{n}y_{j}\left({\frac {\left(\prod _{k=0,k\neq j}^{n}(x-{x}_{k})\right)(x_{j}-x_{n+1})}{\prod _{k=0,k\neq j}^{n+1}(x_{j}-x_{k})}}+{\frac {\left(\prod _{k=0,k\neq j}^{n}(x-{x}_{k})\right)(x-x_{j})}{\prod _{k=0,\,k\neq j}^{n+1}(x_{j}-x_{k})}}\right)+y_{n+1}{\frac {\prod _{k=0}^{n}(x-{x}_{k})}{\prod _{k=0}^{n}(x_{n+1}-x_{k})}}\\&=\sum _{j=0}^{n}y_{j}{\frac {\left(\prod _{k=0,k\neq j}^{n}(x-{x}_{k})\right)(x-x_{n+1})}{\prod _{k=0,k\neq j}^{n+1}(x_{j}-x_{k})}}+y_{n+1}{\frac {\prod _{k=0}^{n}(x-{x}_{k})}{\prod _{k=0}^{n}(x_{n+1}-x_{k})}}\\&=\sum _{j=0}^{n+1}y_{j}\prod _{k=0,k\neq j}^{n+1}{\frac {x-{x}_{k}}{x_{j}-x_{k}}}\\\end{aligned}}\\\end{array}}$

[12] Burden, Richard L.; Faires, J. Douglas. 9th. 2011: 129.

[13] ${\begin{aligned}\triangle ^{k}y_{i}&=\sum _{j=0}^{k}{\frac {k!}{\prod _{l=0,\,l\neq j}^{k}(j-l)}}y_{i+j},\quad 0\leq k\leq n-i\\&=\sum _{j=0}^{k}{\frac {k!}{j!(-1)^{k-j}(k-j)!}}y_{i+j},\quad 0\leq k\leq n-i\\&=\sum _{j=0}^{k}(-1)^{k-j}{\binom {k}{j}}y_{i+j},\quad 0\leq k\leq n-i\end{aligned}}$

[14] Methodus Incrementorum Directa et Inversa（页面存档备份，存于）