高斯定律
高斯定律()表明在闭合曲面内的电荷分佈與產生的電場之間的關係:
- 其微分形式为: ;其中, 为电荷密度(单位 C/m3)。
- 在线性材料中,等式变为 ;其中 为材料的電容率, 為自由電荷密度。
此方程是卡尔·高斯在1835年提出的,但直到1867年才发布。高斯定律在静电场情况下类比于应用在磁场学的安培定律,而二者都被集中在麦克斯韦方程组中。因为数学上的相似性,高斯定律也可以应用于其它由反平方定律决定的物理量,例如引力或者輻照度。参看散度定理。
積分形式
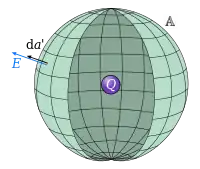
採用國際單位制,對於空間內的任意體積 ,其表面 ,真空中的高斯定律的積分形式可以用方程式表達為
- ;
其中, 为电场, 为閉合曲面 的微分面積,由曲面向外定義為其方向, 是在體積 內的總電荷數量。
- 電通量 是穿過曲面 的電場線數量:
- 。
應用
給予空間的某個區域內,任意位置的電場。原則上,應用高斯定律,可以很容易地計算出電荷的分佈。只要積分電場於任意區域的表面,再乘以真空電容率,就可以得到那區域內的電荷數量。
但是,更常遇到的是逆反問題。給予電荷的分佈,求算在某位置的電場。這問題比較難解析。雖然知道穿過某一個閉合曲面的電通量,這資料仍舊不足以解析問題。在閉合曲面任意位置的電場可能會是非常的複雜。
假若,問題本身顯示出某種對稱性,促使在閉合曲面位置的電場大小變得均勻。那麼,就可以藉著這均勻性來計算電場。像圓柱對稱、平面對稱、球對稱等等,這些空間的對稱性,都能幫助高斯定律來解析問題。若想知道怎樣利用這些對稱性來計算電場,請參閱高斯曲面()。
自由電荷的高斯定律
自由電荷與束縛電荷
自由電荷是自由移動,不被束縛於原子或分子內的電荷;而束縛電荷則是束縛於原子或分子內的電荷。當遇到涉及電介質的問題時,才需要考慮到束縛電荷所產生的效應。當電介質被置入於外電場時,電介質內的束縛電荷會被外電場影響,雖然仍舊束縛於其微觀區域(原子或分子),但會做微小位移。所有這些微小位移的貢獻造成了宏觀的電荷分佈的改變。
雖然微觀而言,不論是自由電荷,還是束縛電荷,本質上都是電荷。實際而言,對於某些案例,使用自由電荷的概念可以簡化問題的解析。但有時候,由於問題比較複雜,缺乏對稱性,必需採用其它方法來解析問題。
微分形式
只涉及自由電荷,這個高斯定律表述的微分形式可以表達為
其中, 是自由電荷密度,完全不包括束縛電荷。
請注意,在某種狀況下,雖然區域內可能沒有自由電荷, 。但是,這並不表示电位移等於 0 。因為,
- ;
其中, 是電極化強度。
取旋度於方程式的兩邊,
- 。
所以,电位移很可能不等於 0 。最典型的例子是永電體。
在數學裏,高斯定律的微分形式等價於其積分形式。這等價關係可以用散度定理來證明。
等價證明
高斯定律與庫侖定律的關係
從庫侖定律推導高斯定律
庫侖定律闡明,一個固定的點電荷的電場是
- ;
其中, 是點電荷, 是電場位置, 是點電荷位置。
根據這方程式,計算位於 的無窮小電荷元素所產生的位於 的電場,積分體積曲域 內所有的無窮小電荷元素,可以得到電荷分佈所產生的電場:
- 。
取這方程式兩邊對於 的散度:
- 。
注意到
- ;
其中,是狄拉克δ函數。
所以, 的散度是
- 。
利用狄拉克δ函數的挑選性質,可以得到高斯定律的微分形式:
- 。
或者可以这样得到高斯定理的积分形式:
点电荷电场通过面元的电通量为
对于单点电荷情形,
( i ) 在高斯面内,
( ii ) 在高斯面外,
故可以得到, ,即
若包围在S面内的电荷具有一定体分布,电荷体密度为,则高斯定理可写成:
由於庫侖定律只能應用於固定不動的電荷,對於移動電荷,這導引不能証明高斯定律成立。事實是,對於移動電荷,高斯定律也成立。所以,從這角度來看,高斯定律比庫侖定律更一般化。
從高斯定律推導庫侖定律
嚴格地說,從高斯定律不能從數學推導出庫侖定律,高斯定律並沒有給出任何關於電場的旋度的資料(參閱亥姆霍茲定理和法拉第電磁感應定律)。但是,假若能夠添加一個對稱性假定,即電荷造成的電場是球對稱的(就像庫侖定律本身一樣,在固定不動電荷的狀況,這假設是正確的;在移動電荷的狀況,這假設是近乎正確的),那麼,就可以從高斯定律推導出庫侖定律。
高斯定律的方程式為
- 。
設定高斯定律積分的曲面 為一個半徑 圓球面,圓心位置在電荷 的位置。那麼,由於球對稱性, , 與 無關,可以將 從積分內提出:
- 。
所以,庫侖定律成立:
- 。
參考文獻
- Griffiths, David J., , Prentice Hall: pp. 326–333, 1998, ISBN 0-13-805326-X
外部連結
- 麻省理工學院物理系影視教學系列:電磁學
