梅滕斯猜想
梅滕斯猜想是数论中的一个猜想,是有關數論中梅滕斯函数上下界的猜想,由汤姆斯·斯蒂尔吉斯在一封于1885年写给夏尔·埃尔米特与弗朗茨·梅滕斯(Franz Mertens)的信中提出。这一猜想如果成立的话可以推出黎曼猜想,不过已被安德鲁·奥德里兹科与赫尔曼·特里尔于1985年证否。
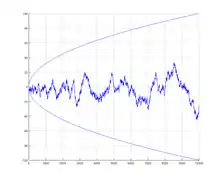
图示为梅滕斯函数的前10000项与默滕斯猜想中的界限。梅滕斯在計算梅滕斯函數的前一萬個值之後,猜想的絕對值恆小於,此猜想被安德鲁·奥德里兹科(Andrew Odlyzko)与赫尔曼·特里尔(Herman te Riele)于1985年证否
猜想的證否
湯姆斯·斯蒂爾吉斯在1885年聲稱已證明比梅滕斯猜想要弱的結果,也就是有界,但其結果沒有發表[1](若用的方式表示,梅滕斯猜想是指)
安德鲁·奥德里兹科与赫尔曼·特里尔在1985年證否了梅滕斯猜想,用的是LLL格缩减算法[2][3]:
- and
參考資料
- Borwein, Peter; Choi, Stephen; Rooney, Brendan; Weirathmueller, Andrea (编). . CMS Books in Mathematics. New York, NY: 施普林格科学+商业媒体. 2007: 69. ISBN 978-0-387-72125-5. Zbl 1132.11047.
- Odlyzko & te Riele (1985)
- Sandor et al (2006) pp.188–189
- Pintz (1987)
- Hurst, Greg. . 2016. arXiv:1610.08551
 [math.NT].
[math.NT]. - Kotnik and Te Riele (2006)
参考文献
- T. Kotnik and Herman te Riele (2006), "The Mertens Conjecture Revisited", Lecture Notes in Computer Science 4076 (Proceedings of the 7th Algorithmic Number Theory Symposium), pp. 156-167.
- T. Kotnik and J. van de Lune (2004), "On the order of the Mertens function", Experimental Mathematics 13, pp. 473-481
- F. Mertens (1897), "Über eine zahlentheoretische Funktion", Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften, Mathematisch-Naturwissenschaftliche Klasse, Abteilung 2a, 106, pp. 761-830.
- Odlyzko, A. M.; te Riele, H. J. J., (PDF), Journal für die reine und angewandte Mathematik, 1985, 357: 138–160 [2012-09-08], ISSN 0075-4102, doi:10.1515/crll.1985.357.138, MR783538, (原始内容存档 (PDF)于2015-09-12)
- Stieltjes, T. J., , Baillaud, B.; Bourget, H. (编), , Paris: Gauthier—Villars: 160–164, 1905
- 埃里克·韦斯坦因. . MathWorld.
- Sándor, József; Mitrinović, Dragoslav S.; Crstici, Borislav (编), , Dordrecht: Springer-Verlag: 187–189, 2006, ISBN 1-4020-4215-9, Zbl 1151.11300
- Pintz, J. (PDF). Astérisque. 1987,. 147–148: 325–333 [2021-10-16]. Zbl 0623.10031. (原始内容存档 (PDF)于2021-04-15).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.