BET理论

多层吸附的BET模型。任意层数的分子在材料表面随机分布。

BET 理论在朗缪尔理论的单分子吸附模型的基础上，基于以下三个假设拓展到多层吸附的情况：

1. 气体分子可以在固体上吸附无数多层；
2. 吸附的各层之间没有相互作用；
3. 朗缪尔吸附理论对每一单分子层成立。

由此得出的BET 吸附等温式如下：

${\displaystyle {\frac {1}{v\left[\left({P_{0}}/{P}\right)-1\right]}}={\frac {c-1}{v_{m}c}}\left({\frac {P}{P_{0}}}\right)+{\frac {1}{v_{m}c}}\ \ \ \ \ \ \ (1)}$

式中，${\displaystyle P,P_{0},v,v_{m}}$ 分别为平衡压强、饱和蒸气压、平衡气体吸附量、单层饱和吸附量，${\displaystyle c}$ 称为 BET 常数，由下式给出。

${\displaystyle c=\exp \left({\frac {E_{1}-E_{L}}{RT}}\right)\ \ \ \ \ \ \ (2)}$

其中 ${\displaystyle E_{1}}$ 是第一层的吸附热，${\displaystyle E_{L}}$ 为其余各层的单层吸附热，数值上等于气体的液化焓。

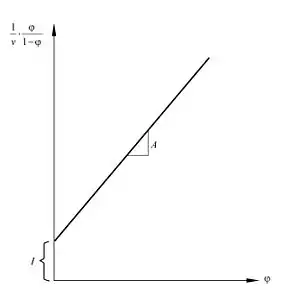
BET plot

根据 (1) 式，在温度恒定的情况下，以 ${\displaystyle {\frac {1}{v\left[\left({P_{0}}/{P}\right)-1\right]}}}$ 对 ${\displaystyle \phi ={P}/{P_{0}}}$ 作图应得一直线，该图称为BET图，实际上，只有在 ${\displaystyle 0.05<{P}/{P_{0}}<0.35}$ 的范围内，BET图表现出较良好的线性。根据直线的斜率 ${\displaystyle A}$ 和截距 ${\displaystyle I}$ 可以求出单层吸附量和 BET 常数，如下两式所示。

${\displaystyle v_{m}={\frac {1}{A+I}}\ \ \ \ \ \ \ (3)}$

${\displaystyle c=1+{\frac {A}{I}}\ \ \ \ \ \ \ (4)}$

BET 吸附等温式广泛用于求算固体材料的表面积。一种固体材料的总表面积 ${\displaystyle S_{total}}$ 与比表面 ${\displaystyle S}$ 由下两式给出，其中 ${\displaystyle v_{m}}$ 为以体积表示的单层饱和吸附量。

${\displaystyle S_{BET,total}={\frac {\left(v_{m}N_{\text{A}}s\right)}{V}}\ \ \ \ \ \ \ (5)}$

${\displaystyle S_{BET}={\frac {S_{total}}{a}}\ \ \ \ \ \ \ (6)}$

${\displaystyle N_{\text{A}}}$: 亞佛加厥常數

${\displaystyle s}$: 吸附物种的吸附截面积

${\displaystyle V}$: 吸附物种的摩尔体积

${\displaystyle a}$: 吸附材料的质量

• 吸附
• 表面张力

1. S. Brunauer, P. H. Emmett and E. Teller, J. Am. Chem. Soc., 1938, 60, 309. doi:10.1021/ja01269a023