树状数组
树状数组或二元索引树(英語:),又以其发明者命名为芬威克樹(英語:),最早由彼得·M·芬威克(Peter M. Fenwick)于1994年以《A New Data Structure for Cumulative Frequency Tables》[1]为题发表在SOFTWARE PRACTICE AND EXPERIENCE。其初衷是解决数据压缩裡的累积频率(Cumulative Frequency)的计算问题,现多用于高效计算数列的前缀和, 区间和。它可以以的时间得到任意前缀和,并同时支持在时间内支持动态单点值的修改。空间复杂度。
| 树状数组 | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 类型 | 二元樹 | ||||||||||||||||
| 发明时间 | 1989年 | ||||||||||||||||
| 发明者 | 鮑里斯·里亞布科 | ||||||||||||||||
| 用大O符号表示的时间复杂度 | |||||||||||||||||
| |||||||||||||||||
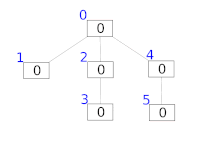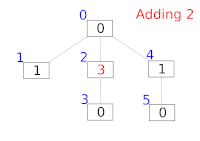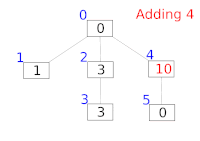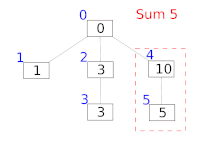
结构起源
按照彼得·M·芬威克的说法,正如所有的整数都可以表示成2的幂和,我们也可以把一串序列表示成一系列子序列的和。采用这个想法,我们可将一个前缀和划分成多个子序列的和,而划分的方法与数的2的幂和具有极其相似的方式。一方面,子序列的个数是其二进制表示中1的个数,另一方面,子序列代表的f[i]的个数也是2的幂。[2][3][4]
基本操作
预备函数
定义一个lowbit函数,返回参数转为二进制后,最后一个1的位置所代表的数值。
例如,lowbit(34)的返回值将是2;而lowbit(12)返回4;lowbit(8)返回8。
将34转为二进制为(0010 0010)2。这里的“最后一个1”指的是从位往前数,见到的第一个1,也就是位上的1。
程序上,(~i + 1) & i表明了最后一位1的值。
仍然以34为例,~(0010 0010)的结果是1101 1101(221),加1后为1101 1110(222),把0010 0010与1101 1110作AND,得0000 0010(2)。
lowbit的一个简便求法:(C++)
int lowbit(int x)
{
return x&(-x);
}
新建
定义一个数组 BIT,用以维护的前缀和,则:
具体能用以下方式实现:(C++)
void build()
{
for (int i = 1; i <= MAX_N; i++)
{
BIT[i] = A[i - 1];
for (int j = i - 2; j >= i - lowbit(i); j--)
BIT[i] += A[j];
}
}
//注:这里的求和将汇集到非终端结点(D00形式)
//BIT中仅非终端结点i值是 第0~i元素的和
//终端结点位置的元素和,将在求和函数中求得
//BIT中的index,比原数组中大1
修改
假设现在要将的值增加delta,
那么,需要将覆盖的区间包含的值都加上delta,
这个过程可以写成递归,或者普通的循环。
需要计算的次数与数据规模N的二进制位数有关,即这部分的时间复杂度是。
修改函数的C++写法:
void edit(int i, int delta)
{
for (int j = i; j <= MAX_N; j += lowbit(j))
BIT[j] += delta;
}
求和
假设我们需要计算的值。
- 首先,将ans初始化为0,将i初始化为k。
- 将ans的值加上
BIT[i]。 - 将i的值减去
lowbit(i)。 - 重复步骤2~3,直到i的值变为0。
求和函数的C/C++写法:
int sum (int k)
{
int ans = 0;
for (int i = k; i > 0; i -= lowbit(i))
ans += BIT[i];
return ans;
}
时空复杂度
- 初始化复杂度最优为:
- 单次询问复杂度:,其中N为数组大小
- 单次修改复杂度:,其中N为数组大小
- 空间复杂度:
扩展
树状数组可以通过维护差分数组来处理区间修改和单点查询。具体地,当我们在 增加 时只需执行 edit(l,d) 和 edit(r+1,-d) 。查询则与单点修改区间查询相似。