施特拉森演算法
簡介
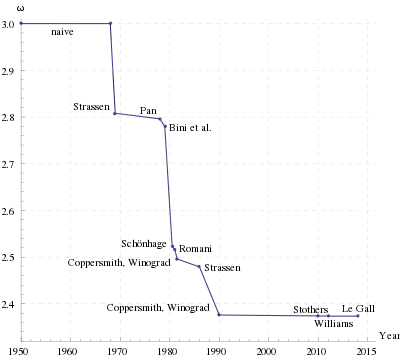
矩陣乘法演算法的演進。
施特拉森演算法在1969年由沃爾克·施特拉森所提出,是第一個時間複雜度低於的矩陣乘法演算法。由於演算法簡單理解,且為第一個被提出來的特性,常被演算法教材拿來當作主定理(英語:)計算時間複雜度的例子。
另外,因為施特拉森演算法證明了矩陣乘法存在時間複雜度低於的演算法,使得更多學者投入研究,尋找更快的演算法。
算法
計算
將A, B, C分成相等大小的方塊矩陣:
即
於是
引入新矩陣
可得:
其中的計算也是使用施特拉森演算法求得。
評論
一般矩陣乘法的時間複雜度為,施特拉森演算法因為只有每次的分治法(英語:)只有七個矩陣乘法運算,所以依照主定理(英語:)可以得出時間複雜度為。但Strassen演算法的數值穩定性較差。
現時時間複雜度最低的矩陣乘法演算法是Coppersmith-Winograd方法的一种扩展方法,其算法复杂度为)。[1]
相關連結
参考来源
- Virginia Vassilevska Williams. (PDF). [2014-01-14]. (原始内容存档 (PDF)于2013-10-08).而1990年Coppersmith-Winograd方法提出时的算法复杂度为。
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.