事件視界
事件視界(英語:),亦稱事件穹界,是一種時空的曲隔界線。
.jpg.webp)
視界中任何的事件皆無法對視界外的觀察者產生影響,在黑洞周圍的便是事件視界。
在非常巨大的重力影響下,黑洞附近的逃逸速度大于光速,使得任何光線皆不可能從事件視界內部逃脫。
根據廣義相對論,在遠離視界的外部觀察者眼中,任何從視界外部接近視界的物件,將需要用無限長的時間到達視界面,其影像會經歷無止境逐漸增強的紅移;但該物件本身卻不會感到任何異常,並會在有限時間之內穿過視界。
阿赫麦德·阿姆黑利(Ahmed Almheiri)、唐纳德·马若夫(Donald Marolf)、约瑟夫·波尔钦斯基(Joseph Polchinski)、詹姆斯·苏利(James Sully)近年的研究認為事件視界會造成黑洞火牆,而火牆的存在跟黑洞本身相矛盾。[1]
其他相關但不同的視界包括同樣可以在黑洞旁找到的絕對視界線與視視界。另有一些相關的名詞包括柯西與基林視界、 克爾度規中的動圈、宇宙學中的宇宙學視界等。
黑洞的事件視界
 遠離黑洞的粒子可以隨意地向各方向移動,僅僅有光速為其速度上限這一限制。 |
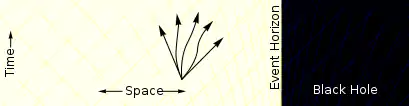 時空在靠近黑洞的地方開始變形。在一些坐標系中,向黑洞移動的路徑多過於遠離黑洞的路徑。[Note 1] |
 在事件視界中所有的路徑都是朝向黑洞中心,沒有粒子可以脫離。 |
事件視界最有名的例子來自於廣義相對論中對於黑洞的描述:一個質量大到附近的物質或輻射無法逃離其重力場的天體。通常,這個邊界是當對於黑洞的脫離速度大於光速的位置。然而,更精確的描述是在這個視界中,所有的光錐都已經變形朝向黑洞中心。一旦粒子進入視界中,朝向黑洞運行與在時間中前行時一樣不可避免的,而兩者在某些坐標系底下甚至是一樣的。[3][4]
大小为史瓦西半徑的物体表面便是一個不轉動的黑洞的事件視界(轉動的黑洞的行為稍有不同)。一個物體的史瓦西半徑正比於其質量。理論上來說,任何有質量的物體都可以被壓縮成一個黑洞,只要我們將所有的質量壓縮進其對應的史瓦西半徑大小的空間中。例如太陽的史瓦西半徑大約是3公里長,而地球的史瓦西半徑約为9毫米。[5]然而實際上來說,地球與太陽都不具備足夠大的質量來抵抗如此高密度的情形下產生的電子與中子簡併壓力。要克服這樣的壓力而形成黑洞所需要的質量稱之為歐本海默極限,大約需要至少3倍于太陽的質量。[6]
然而,與黑洞事件視界的觀念常常被誤解。人們通常錯誤地認為黑洞會將物質抽入真空,實際上黑洞對於物質的吸引力與其他具有重力的物質皆一樣。另外一個常常被誤解的概念是認為人們可以觀測到物質掉入黑洞的過程,這卻是不可能的。天文學家僅僅可以看到黑洞附近的吸積盤,因為這裡物質高速運動所產生的高能輻射可以被人們觀測。另外,遙遠的觀測者並不可能看到物質跨越事件視界,而僅僅能看到物質以越來越慢的速度靠近它。[3]
宇宙學視界
在宇宙學中也有不同的視界。其中宇宙學的事件視界是位於可觀測宇宙中同移距離最遠處,也就是「現在」所放出的光子將能被未來的觀測者看到的最遠距離處。[7]這與另外一個宇宙學中的視界,粒子視界,的觀念是不同的。粒子視界是在給定某個時間的觀測者後,過去釋放的粒子仍舊能到達這個觀測者的最遠同移距離處。在粒子視界更遠處,即便是宇宙剛誕生時就發出的光子將不能再到達這個觀測者。[8] 而宇宙學視界的位置與時間的關係是根據宇宙膨脹所決定的。當宇宙的膨脹具備特定的性質,無論觀測者等待多久時間,部分的宇宙將永遠無法被觀測。
到事件視界的同移距離對的函數為:[9]
在這個公式中,""是宇宙標度因子、""是光速、""是時空坐標系時間軸的重點,若宇宙永遠膨脹下去,則這個值為無限大。
然而也有宇宙學的模型是沒有事件視界存在的,一個例子便是德西特宇宙模型。 關於宇宙學視界具體的計算被詳細的記錄在關於FLRW宇宙學模型的論文中,一個以狀態方程近似宇宙的模型。[8][10]
加速粒子的相對視界

若一個粒子在不膨脹的宇宙中以等速移動且不受到重力場作用,那麼那個宇宙中發生的任何事件將終究被這個粒子所看到,因為這些事件前方的光錐與粒子的世界線有所交集。
另一方面,若粒子在加速運動,某些情況下事件的光錐並不會與粒子的世界線有所交集。
在這樣的情況下,我們說一個相對視界出現在粒子的(加速)參考坐標系中,代表著一個事件無法被粒子觀測到的邊界。
例如說,一個等加速度運動的粒子便會有相對視界。
右圖展示了這個情況的一個示意圖。當一個粒子加速時,他會越來越接近光速,但並無法相對於他自己的參考坐標系達到光速。
圖中,他的軌跡是一個雙曲線,而雙曲線的漸近線是一條45度的直線。
若一個事件的光錐的邊緣是在這個漸近線以內的話那他便無法被這個粒子所觀測。
從粒子的角度來說,那裡便形成了一個沒有訊號可以逃出的邊界,稱之為相對視界。
在日常生活中視界並不會出現,因為這需要無限地加速粒子,也就代表我們需要無限的能量以及無限大的器材。
與事件視界的交互作用
人們常常認為事件視界,特別是黑洞的事件視界是一個會摧毀接近其物質的不可變界面。
實際上,所有事件視界的觀念都是對於遠離其的觀測者來說的,接近事件視界的物體則自身從不會感受到自己跨越了事件視界(也就是跨越視界這個事件的光錐和觀測者的世界線永不相交)。[11]
對於一個在寬廣空間以等加速度運動的觀測者來說,無論周圍的物質如何移動,視界看起來都在一個固定的距離外。若是改變觀測者的加速度則視界的位置便可能有所變動。
另外,觀測者永遠不會碰觸到視界也不會跨越視界。[3]若觀測者是居住在德西特宇宙中的一個慣性坐標的話,那麼視界的位置也將維持固定不變。[12]
當討論的是黑洞的視界時,位處遙遠且相對靜止的觀測者將看到處在同個位置的事件視界。
這似乎可以允許觀測者降下一根繩子讓他碰觸事件視界,因為到視界的距離是有限的,所以僅僅需要有限長的繩子便可以達成。
實際上這卻無法辦到,若是緩慢的垂下繩子(也就是繩子上的每一點在史瓦西坐標中是相對靜止的),越靠近視界的繩子上每一點所受到的加速度(G力)便將越趨近於無限大,于是繩子便會被撕裂。
若是快速的降下繩子,那麼繩子的底端確實可以接觸甚至跨越視界。
但一旦這發生了,觀測者將無法再將繩子拉回,因為拉回繩子必定將會拉緊繩子,然而假設繩子是拉緊的,那麼繩子上的張力將隨著靠近視界的距離無限增大並在某處拉斷繩子。
並且,繩子斷裂的地方不會發生在事件視界上而是在一個可以被觀測者所看到的地方。[13]
附註
- 這些由可能的路徑所構成的集合,或稱之為未來光錐,包含所有可能的世界線(在圖中以黃/藍色的格線表示)。他們依照愛丁頓–芬克爾斯坦坐標系的方式傾斜(圖示是一個愛丁頓–芬克爾斯坦坐標系的卡通版本),然而在其他坐標系中光錐不一定要這樣傾斜。例如說在史瓦西坐標系中,光錐僅僅是變窄而不會因為靠近事件視界而傾斜。在克魯斯卡爾坐標系中,光錐甚至不改變形狀及其指向。[2]
參考文獻
- . [2018-03-17]. (原始内容存档于2019-05-02). (页面存档备份,存于)
- Misner, Thorne & Wheeler 1973,第848頁
- . [2017-01-16]. (原始内容存档于2019-05-02). (页面存档备份,存于)
- . [2017-01-16]. (原始内容存档于2014-09-16). (页面存档备份,存于)
- . [2017-01-16]. (原始内容存档于2018-11-11). (页面存档备份,存于)
- I. Bombaci. . Astronomy and Astrophysics. 1996, 305: 871–877. Bibcode:1996A&A...305..871B.
- Lars Bergström and Ariel Goobar: "Cosmology and Particle Physics", WILEY (1999), page 65.ISBN 0-471-97041-7
- Margalef-Bentabol, Berta; Margalef-Bentabol, Juan; Cepa, Jordi. . Journal of Cosmology and Astroparticle Physics. 015. 2013-02-08, 2013 (02) [2017-01-16]. Bibcode:2013JCAP...02..015M. arXiv:1302.2186
 . doi:10.1088/1475-7516/2013/02/015. (原始内容存档于2019-12-08). (页面存档备份,存于)
. doi:10.1088/1475-7516/2013/02/015. (原始内容存档于2019-12-08). (页面存档备份,存于) - Massimo Giovannini. . World Scientific. 2008: 70– [2011-05-01]. ISBN 978-981-279-142-9. (原始内容存档于2019-05-02). (页面存档备份,存于)
- Margalef-Bentabol, Berta; Juan Margalef-Bentabol; Jordi Cepa. . Journal of Cosmology and Astroparticle Physics. 2012-12-21, 2012 (12): 035 [2017-01-16]. Bibcode:2012JCAP...12..035M. arXiv:1302.1609
 . doi:10.1088/1475-7516/2012/12/035. (原始内容存档于2019-12-08). (页面存档备份,存于)
. doi:10.1088/1475-7516/2012/12/035. (原始内容存档于2019-12-08). (页面存档备份,存于) - . [2017-01-16]. (原始内容存档于2020-11-11). (页面存档备份,存于)
-
Berestovskii, Valera; Irina Zubareva. . arXiv:1406.3239
 .
. - Charles Misner, Kip Thorne, and John Wheeler (1973). Gravitation, p. 824
延伸閱讀
- 史蒂芬·霍金. . 大塊文化. 2001.
- 基普·索恩. . 湖南科學技術出版社. 2000.
- Abhay Ashtekar and Badri Krishnan, “Isolated and Dynamical Horizons and Their Applications”, Living Rev. Relativity, 7, (2004), 10; Online Article, cited Feb.2009.