信賴區間
在统计学中,一个概率样本的置信区间(英語:,),是对产生这个样本的总体的参数分布()中的某一个未知母數值,以区间形式给出的估计。相对于点估计()用一个样本统计量来估计参数值,置信区间还蕴含了估计的精确度的信息。在现代机器学习中越来越常用的置信集合()概念是置信区间在多维分析的推广[1]。
置信区间在频率学派中间使用,其在贝叶斯统计中的对应概念是可信区间()。两者建立在不同的概念基础上的,贝叶斯统计将分布的位置参数视为随机变量,并对给定观测到的数据之后未知参数的后验分布进行描述,故无论对随机样本还是已观测数据,构造出来的可信区间,其可信水平都是一个合法的概率[2];而置信区间的置信水平,只在考虑随机样本时可以被理解为一个概率。
定义
对随机样本的定义
定义置信区间最清晰的方式是从一个随机样本出发。考虑一个一维随机变量服从分布,又假设是的参数之一。假设我们的数据采集计划将要独立地抽样次,得到一个随机样本,注意这里所有的都是随机的,我们是在讨论一个尚未被观测的数据集。如果存在统计量(统计量定义为样本的一个函数,且不得依赖于任何未知参数)满足使得:
则称为一个用于估计参数的置信区间,其中的,称为置信水平,在假设检验中也称为显著性水平。
对观测到的数据的定义
接续随机样本版本的定义,现在,对于随机变量的一个已经观测到的样本,注意这里用小写x表记的都是已经观测到的数字,没有随机性了,定义基于数据的置信区间为:
注意,置信区间可以是单尾或者双尾的,单尾的置信区间中设定或者,具体前者还是后者取决于所构造的置信区间的方向。
初学者常犯一个概念性错误,是将基于观测到的数据所同样构造的置信区间的置信水平,误认为是它包含真实未知参数的真实值的概率。正确的理解是:置信水平只有在描述这个同样构造置信区间的过程(或称方法)的意义下才能被视为一个概率。一个基于已经观测到的数据所构造出来的置信区间,其两个端点已经不再具有随机性,因此,类似的构造的间隔将会包含真正的值的比例在所有值中,其包含未知参数的真实值的概率是0或者1,但我们不能知道是前者还是后者[3]。
例子
例1:正态分布,已知总体方差
水平的正态置信区间为:
- (双尾)
- (单尾)
- (单尾)
以下为方便起见,只列出双尾置信区间的例子,且区间中用""进行简记:
例2:正态分布,未知总体方差
水平的双尾正态置信区间为:
例3:两个独立正态样本
設有兩個獨立正態樣本和,样本大小为和,估计总体均值之差,假设总体方差未知但相等:(如果未知且不等就要应用Welch公式来确定t分布的自由度) 水平的双尾正态置信区间为:
- ,其中且分别表示和的样本标准差。
常見誤解
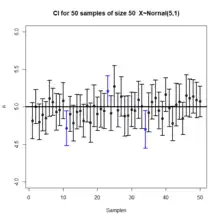
信賴區間及信心水準常被誤解,出版的研究也顯示出既使是專業的科學家也常做出錯誤的詮釋。[4][5][6][7][8][9]
- 以95%的信賴區間來說,建構出一個信賴區間,不代表分佈的參數有95%的機率會落在該信賴區間內(也就是說該區間有95%的機率涵蓋了分佈參數)。 [10]依照嚴格的頻率學派詮釋,一旦信賴區間被建構完全,此區間不是涵蓋了參數就是沒涵蓋參數,已經沒有機率可言。95%機率指的是建構信賴區間步驟的可靠性,不是針對一個特定的區間。[11]內曼本人(信賴區間的原始提倡者)在他的原始論文提出此點:[12]
「在上面的敘述中可以注意到,機率是指統計學家在未來關心的估計問題。事實上,我已多次說明,正確結果的頻率會趨向於α。考慮到一個樣本已被抽取,[特定端點]也已被計算完成。我們能說在這個特定的例子裡真值[落到端點中]的機率等於α嗎?答案明顯是否定的。參數是未知的常數,無法做出對其值的機率敘述……」
- Deborah Mayo針對此點進一步說道:[13]
「無論如何必須強調,在看到[資料的]數值後,Neyman–Pearson理論從不允許做出以下結論,特定產生的信賴區間涵蓋了真值的機率或信心為(1 − α)100%。Seidenfeld的評論似乎源於一種(並非不尋常的)期望,Neyman–Pearson信賴區間能提供他們無法合理提供的,也就是未知參數落入特定區間的機率大小、信心高低或支持程度的測度。隨著Savage (1962)之後,參數落入特定區間的機率可能是指最終精密度的測度。最終精密度的測度令人嚮往而且信賴區間又常被(錯誤地)解釋成可提供此測度,然而此解釋是不被保證的。無可否認的,『信賴』二字助長了此誤解。」
- 95%信賴區間不代表有95%的樣本資料落在此信賴區間。
- 信賴區間不是樣本參數的可能值的確定範圍,雖然它常被啟發為可能值的範圍。
- 從一個實驗中算出的一個95%信賴區間,不代表從不同實驗得到的樣本參數有95%落在該區間中 [8]
构造法
一般来说,置信区间的构造需要先找到一个枢轴变量(,或称),其表达式依赖于样本以及待估计的未知参数(但不能依赖于总体的其它未知参数),其分布不依赖于任何未知参数。
下面以上述例2为例,说明如何利用枢轴变量构造置信区间。对于一个正态分布的随机样本,可以证明(此证明对初学者并不容易)如下统计量互相独立:
- 和
它们的分布是:
- 和
所以根据t分布的定义,有
于是反解如下等式左边括号中的不等式
就得到了例2中双尾置信区间的表达式。
与参数检验的联系
有时,置信区间可以用来进行母數检验。例如在上面的例1中构造的双尾水平置信区间,可以用来检验具有相应的显著水平为的双尾對立假說,具体地说是如下检验: 正态分布总体,知道总体方差,在显著水平下检验:
- vs
检验方法是:当(且仅当)相应的水平置信区间不包含时拒绝零假设
例1中构造的双尾水平置信区间也可以用来检验如下两个显著水平为的单尾对立假设:
- vs
和
- vs
检验方法是完全类似的,比如对于上述第一个单尾检验,当且仅当双尾置信区间的左端点大于时拒绝零假设。
参考文献
- Brittany Terese Fasy; Fabrizio Lecci; Alessandro Rinaldo; Larry Wasserman; Sivaraman Balakrishnan; Aarti Singh. . The Annals of Statistics. 2014, 42 (6): 2301–2339.
- Box, George EP; Tiao, George C. . John Wiley & Sons. 2011.
- Moore, D; McCabe, George P; Craig, B. . San Francisco, CA: Freeman. 2012.
- Kalinowski, Pawel. (PDF). 2010 [2021-12-22]. (原始内容 (PDF)存档于2022-01-21).
- (PDF). [2014-09-16]. (原始内容 (PDF)存档于2016-03-04).
- Hoekstra, R., R. D. Morey, J. N. Rouder, and E-J. Wagenmakers, 2014. Robust misinterpretation of confidence intervals. Psychonomic Bulletin Review, in press. (页面存档备份,存于)
- Scientists’ grasp of confidence intervals doesn’t inspire confidence (页面存档备份,存于), Science News, July 3, 2014
- Greenland, Sander; Senn, Stephen J.; Rothman, Kenneth J.; Carlin, John B.; Poole, Charles; Goodman, Steven N.; Altman, Douglas G. . European Journal of Epidemiology. April 2016, 31 (4): 337–350. ISSN 0393-2990. PMC 4877414
 . PMID 27209009. doi:10.1007/s10654-016-0149-3.
. PMID 27209009. doi:10.1007/s10654-016-0149-3. - Helske, Jouni; Helske, Satu; Cooper, Matthew; Ynnerman, Anders; Besancon, Lonni. . IEEE Transactions on Visualization and Computer Graphics (Institute of Electrical and Electronics Engineers (IEEE)). 2021-08-01, 27 (8): 3397–3409. ISSN 1077-2626. PMID 33856998. S2CID 233230810. arXiv:2002.07671
 . doi:10.1109/tvcg.2021.3073466.
. doi:10.1109/tvcg.2021.3073466. - Morey, R. D.; Hoekstra, R.; Rouder, J. N.; Lee, M. D.; Wagenmakers, E.-J. . Psychonomic Bulletin & Review. 2016, 23 (1): 103–123. PMC 4742505
 . PMID 26450628. doi:10.3758/s13423-015-0947-8.
. PMID 26450628. doi:10.3758/s13423-015-0947-8. - . nist.gov. [2014-09-16]. (原始内容存档于2008-02-05).
- Neyman, J. . Philosophical Transactions of the Royal Society A. 1937, 236 (767): 333–380. Bibcode:1937RSPTA.236..333N. JSTOR 91337. doi:10.1098/rsta.1937.0005
 .
. - Mayo, D. G. (1981) "In defence of the Neyman–Pearson theory of confidence intervals" (页面存档备份,存于), Philosophy of Science, 48 (2), 269–280.
参考书目
- 羅納德·費雪 (1956) Statistical Methods and Scientific Inference. Oliver and Boyd, Edinburgh. (See p. 32.)
- 弗罗因德 (1962) Mathematical Statistics Prentice Hall, Englewood Cliffs, NJ. (See pp. 227–228.)
- 伊安·海金 (1965) Logic of Statistical Inference. Cambridge University Press, Cambridge
- 齐平 (1962) Introduction to Statistical Inference. D. Van Nostrand, Princeton, NJ.
- 杰克·基弗(1977) "Conditional Confidence Statements and Confidence Estimators (with discussion)" Journal of the American Statistical Association, 72, 789–827.
- 泽西·内曼 (1937) "Outline of a Theory of Statistical Estimation Based on the Classical Theory of Probability" Philosophical Transactions of the Royal Society of London A, 236, 333–380. (Seminal work.)
- G.K.罗宾逊 (1975) "Some Counterexamples to the Theory of Confidence Intervals." Biometrika, 62, 155–161.