协方差矩阵
在统计学与概率论中,协方差矩阵(covariance matrix)是一个方阵,代表著任兩列随机变量间的协方差,是协方差的直接推广。

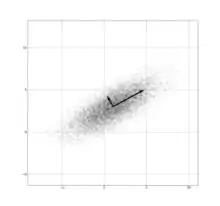
中心为 (0, 0) 的一个二元高斯概率密度函数,协方差矩阵为 [ 1.00, 0.50 ; 0.50, 1.00 ]。
定义
將之以矩形表示的話就是:
根據測度積分的線性性質,协方差矩阵還可以進一步化簡為:
矩陣表示法
以上定義所述的隨機變數序列 和 ,也可分別以用行向量 與 表示,換句話說:
這樣的話,對於 個定義在 上的隨機變數 所組成的矩陣 , 定義:
也就是說
那上小節定義的协方差矩阵就可以記为:
所以协方差矩阵也可對 與 來定義:
性质
有以下的基本性质:
尽管共變異數矩阵很简单,可它却是很多领域里的非常有力的工具。它能导出一个变换矩阵,这个矩阵能使数据完全去相关(decorrelation)。从不同的角度看,也就是说能够找出一组最佳的基以紧凑的方式来表达数据。(完整的证明请参考瑞利商)。 这个方法在统计学中被称为主成分分析(principal components analysis),在图像处理中称为Karhunen-Loève 变换(KL-变换)。
複随机向量
均值为的複随机标量变量的方差定义如下(使用共轭複数):
其中复数的共轭记为。
如果 是一个复列向量,则取其共轭转置,得到一个方阵:
其中为共轭转置, 它对于标量也成立,因为标量的转置还是标量。
估计
多元正态分布的共變異數矩阵的估计的推导非常精致. 它需要用到谱定义以及为什么把标量看做矩阵的迹更好的原因。参见共變異數矩阵的估计。
外部链接
- Covariance Matrix(页面存档备份,存于) at Mathworld
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.