卜瓦松分布
泊松分布(法語:;英語:)又稱Poisson分布、分布、布瓦松分布、布阿松分布、普阿松分布、波以松分布、卜氏分布、帕松小數法則(Poisson law of small numbers),是一種統計與概率學裡常見到的離散機率分布,由法國數學家西莫恩·德尼·泊松在1838年時發表。
|
质量函數 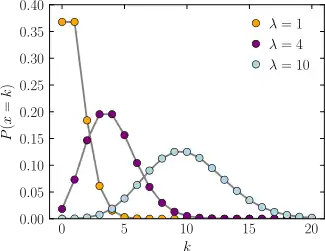 横轴是索引k,发生次数。该函数只定义在k为整数的时候。连接线是只为了指导视觉。 | |||
|
累積分布函數 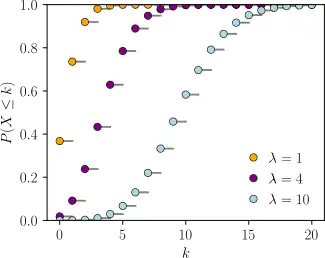 横轴是索引k,发生次数。CDF在整数k处不连续,且在其他任何地方都是水平的,因为服从泊松分布的变量只针对整数值。 | |||
| λ > 0(实数) | |||
| 值域 | |||
| 累積分布函數 |
,或,或 (对于,其中是不完全Γ函数,是高斯符号,Q是规则化Γ函数) | ||
| 期望值 | |||
| 中位數 | |||
| 眾數 | |||
| 偏度 | |||
| 峰度 | |||
| 熵 |
(假设较大) | ||
| 特徵函数 | |||
泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。如某一服务设施在一定时间内受到的服务请求的次数,电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数、放射性原子核的衰变数、雷射的光子數分布等等。(單位時間內發生的次數,可以看作事件發生的頻率,類似物理的頻率)。
泊松分布的機率質量函数为:
泊松分布的参数是随机事件发生次数的数学期望值。
记号
若服从参数为的泊松分布,记为,或记为.
性质
1、服从泊松分布的随机变量,其数学期望与方差相等,同为参数 :
2、兩個獨立且服从泊松分布的随机变量,其和仍然服从泊松分布。更精確地說,若 且 ,則。反過來若兩個獨立隨機變量的和服從卜瓦松分布,則這兩個隨機變量經平移後皆服從卜瓦松分布(Raikov定理)。
3、其動差母函數为:
泊松分布的来源(泊松小数定律)
在二项分布的伯努利试验中,如果试验次数很大,二项分布的概率很小,且乘积比较适中,则事件出现的次数的概率可以用泊松分布来逼近。事实上,二项分布可以看作泊松分布在离散時間上的对应物。
证明如下。首先,回顾自然對數的定义:
二项分布的定义:
- 。
如果令, 趋于无穷时的极限:
最大似然估計(MLE)
给定个样本值,希望得到从中推测出总体的泊松分布参数的估计。为计算最大似然估计值,列出对数似然函数:
解得λ从而得到一个驻点(stationary point):
检查函数的二阶导数,发现对所有的与大于零的情况二阶导数都为负。因此求得的驻点是对数似然函数的极大值点:
例子
对某公共汽车站的客流做调查,统计了某天上午10:30到11:47来到候车的乘客情况。假定来到候车的乘客各批(每批可以是1人也可以是多人)是互相独立发生的。观察每20秒区间来到候车的乘客批次,共观察77分钟*3=231次,共得到230个观察记录。其中来到0批、1批、2批、3批、4批及4批以上的观察记录分别是100次、81次、34次、9次、6次。使用极大似真估计(MLE),得到的估计为。
生成泊松分布的随机变量
一个用来生成随机泊松分布的数字(伪随机数抽样)的简单算法,已经由高德纳给出(见下文参考):
algorithm poisson random number (Knuth):
init:
Let L ← e−λ, k ← 0 and p ← 1.
do:
k ← k + 1.
Generate uniform random number u in [0,1] and let p ← p×u.
while p > L.
return k − 1.
尽管简单,但复杂度是线性的,在返回的值,平均是。还有许多其他算法来克服这一点。有些人由Ahrens和Dieter给出,请参阅下面的参考资料。同样,对于较大的值,可能导致数值稳定性问题。对于较大值的一种解决方案是拒绝采样,另一种是采用泊松分布的高斯近似。
对于很小的值,逆变换取样简单而且高效,每个样本只需要一个均匀随机数u。直到有超过的样本,才需要检查累积概率。
algorithm Poisson generator based upon the inversion by sequential search:[1]
init:
Let x ← 0, p ← e−λ, s ← p.
Generate uniform random number u in [0,1].
do:
x ← x + 1.
p ← p * λ / x.
s ← s + p.
while u > s.
return x.
参考文献
引用
- Luc Devroye, Non-Uniform Random Variate Generation(Springer-Verlag, New York, 1986), chapter 10, page 505 http://luc.devroye.org/rnbookindex.html (页面存档备份,存于)
来源
- Guerriero V. . Journal of Modern Mathematics Frontier (JMMF). 2012, 1: 21–28 [2017-10-30]. (原始内容存档于2018-02-21).
- Joachim H. Ahrens, Ulrich Dieter. . Computing. 1974, 12 (3): 223–246. doi:10.1007/BF02293108.
- Joachim H. Ahrens, Ulrich Dieter. . ACM Transactions on Mathematical Software. 1982, 8 (2): 163–179. doi:10.1145/355993.355997.
- Ronald J. Evans, J. Boersma, N. M. Blachman, A. A. Jagers. . SIAM Review. 1988, 30 (2): 314–317. doi:10.1137/1030059.
- Donald E. Knuth. . The Art of Computer Programming. Volume 2. Addison Wesley. 1969.