多重宇宙論
多重宇宙論(英語:),指的是一種在物理學裡尚未證實的假說。在我們的宇宙之外,很可能還存在著其他的宇宙,而這些宇宙是宇宙的可能狀態的一種反應,這些宇宙可能其基本物理常數和我們所認知的宇宙相同,也可能不同。一個普遍的假設是,多元宇宙是「由不同的宇宙拼湊而成的被子,所有宇宙都受到相同的物理定律的約束」[1]。多重宇宙這個名詞是由美國哲學家與心理學家威廉·詹姆士在1895年所提出的[2]。
平行宇宙經常被用以說明:一個事件不同的過程或一個不同的決定的後續發展是存在於不同的平行宇宙中的;這個理論也常被用於解釋其他的一些悖论,像關於時間旅行的一些悖论,像「一顆球落入時光隧道,回到過去撞上了自己因而使得自己無法進入時光隧道」,解決此詭論除了假設時間旅行是不可能外,也可以以平行宇宙作解釋,而根據平行宇宙理論,這顆球撞上自己和沒有撞上自己是兩個不同的平行宇宙。
平行宇宙的分類
2003年的《科學美國人》雜誌中,有一篇由美國宇宙學家马克斯·泰格马克撰寫的有關平行宇宙的專文,文中他將平行宇宙分成4類[3][4]:
- 第一類:這一類宇宙和我們的宇宙的物理常數相同,但是粒子的排列法不同,同時這一類宇宙亦可以被視為存在於已知的宇宙(可觀測宇宙)之外的地方。
- 第二類:這一類宇宙的物理定律大致和我們的宇宙相同,但是基本的物理常數並不同。
- 第三類(艾弗雷特的多世界詮釋):根據量子理論,一件事件發生之後可以產生不同的後果,而所有可能的後果都會形成一個宇宙,而這一類宇宙可以被歸屬於第一類或第二類的平行宇宙,因為這一類宇宙所遵守的基本物理定律依然和我們所認知的宇宙相同(上述「一顆球落入時光隧道,回到過去撞上了自己,因而使自己無法進入時光隧道」詭論的平行宇宙解決辦法屬於這一種)。
- 第四類(數學宇宙假說):這一類宇宙最基礎的物理定律和我們的宇宙不同,而基本上到第四類為止,就可以解釋到所有可能存在(也就是可想像得到的)的宇宙,一般而言,這些宇宙的物理定律可以利用M理論構造出來。
相關理論
雙宇宙(鏡像反宇宙)理論

有兩個相關宇宙的模型,例如,試圖用鏡像反宇宙來解釋重子不對稱性——為什麼一開始物質多於反物質[5][6][7]。一個雙宇宙宇宙學模型可以通過兩個世界之間的相互作用來解釋哈勃常數(H0)張力。「鏡像世界」將包含所有現有基本粒子的副本[8][9]。另一個孿生/對世界或「雙世界」宇宙學在理論上被證明能夠解決與暗能量密切相關的宇宙學常數(Λ)問題:兩個相互作用的世界,每個世界都有較大的Λ,可以產生一個小的共用有效Λ[10][11][12]。
無窮宇宙(開放宇宙)理論
開放宇宙理論認為,我們目前所知道的宇宙只是整個宇宙中可觀測的一小部份。在這個部份以外,整個宇宙尚有無限大的未被觀測的空間;根據相對論,光速為宇宙最快的速度,我們所看到的部份(可觀測宇宙)是已經到達地球的光線,要注意的是,可观测的宇宙并不等于哈伯體積,哈伯體積直接取決於宇宙的年齡(因為若果宇宙誕生於N年前,則能到達地球的光線最遠只能在N光年處,更遠的光線則尚在路途上,故未能被地球上的觀測者所觀測),哈伯體積的膨脹是因為有越來越遠處的光線到達地球。 且根據馬克斯·泰格马克的推論,在距離約1010118公尺的宇宙的遠方(此值是根據質子配置而可能出現的模式總數所算出)可能有「另一個地球」「另一個自己」,換句話說,就是存有與我們可觀測宇宙(半徑約4.4×1026米)完全相同的分身,亦即開放宇宙理論說明了第一類平行宇宙的可能性。
泡沫宇宙理論

泡沫宇宙理論認為存在有無限多的開放宇宙,而這些開放宇宙本身有著不同的物理常數,這些開放宇宙的「距離」比我們的開放宇宙的「邊緣」還要遠,意即這些宇宙存在於無窮遠的地方之外。
這個理論由安德烈·林德最早提議,而泡沫宇宙理論本身能和暴脹理論在相當程度上契合,而這個理論本身牽涉到宇宙可能是由某個「親宇宙」的量子泡沫中所誕生的可能,而這些量子泡沫產生於能量的起伏,這些能量的起伏可能會產生微小的「泡沫」和蟲洞。若這些「泡沫」不是非常巨大,它們會像膨脹的汽球般,到了最後消失無蹤,不過如果能量起伏大於某個常數,這個泡沫就會不斷膨脹,甚而產生一個「子宇宙」,而「子宇宙」的體積可能大到足以讓宇宙大尺度結構存在的地步。
2005年,美国的理论物理学家Laura Mersini-Houghton和Richard Holman预言宇宙辐射存在不规则分布的原因是其他宇宙的牵引。普朗克天文望远镜的宇宙背景辐射图在理论上是分布均匀的,但实际结果显示南半部天空中存在一个强大的中心,以及一个无法用现有物理学知识解释的冷斑点。Mersini-Houghton认为这证实了自己的预测[13]。
大反彈理論
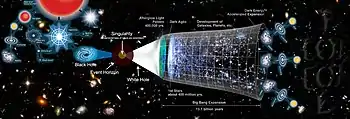
根據迴圈量子重力理論,大爆炸可能只是宇宙不斷膨脹和收縮的週期中,一個新的膨脹時期的開始而已。每個週期開始於大爆炸、結束於大擠壓(Big Crunch),而這個週期的輪迴是無限的,稱為「振蕩宇宙」。在大爆炸之後宇宙膨脹,而之後在重力的作用之下宇宙開始收縮,然後接著是大擠壓,在大擠壓之後的下一次大爆炸被稱為大反彈,雖然這個模型曾經一度被否決,但是膜宇宙論近年來已重拾此模型(振蕩宇宙模型)。
在每個週期中,宇宙可能會有不同的宇宙常數,而因此這些不同週期時的宇宙可視為第二種平行宇宙。
泡沫宇宙理論和大反彈理論使第二種平行宇宙的存在成為可能。
量子力學的多世界解釋
量子力學的多世界解釋是一種主要的量子力學解釋,在由此解釋方式中的眾平行宇宙共有一個關於時間的變數,而這些平行宇宙彼此之間有著相同的起源,而這些宇宙彼此之間的基本物理定律相同,但物理常數可能會有所不同,而它們亦可能處於不同的狀態,而且這些宇宙彼此之間沒有任何的聯繫,因此它們彼此之間沒有任何訊息互通,這些宇宙彼此之間的關係由它們之間的疊加態決定。
此理論為第三類平行宇宙的基礎。
M理論
根據M理論,我們的宇宙很可能是產生於11維薄膜的碰撞與撕裂當中,基本上由此產生的宇宙可以和多世界詮釋裡所說的宇宙極為不同的宇宙。
由M理論可推出第四種平行宇宙的存在。
弦論「地景」
根據IIB型弦論,從十維弦論的世界到我們所知的四維世界有極多種的變換方式,而不同的變換方式會產生相當不同的宇宙。
搜索證據
在1990年代,在當時關於這個概念的小說作品流行起來之後,關於多重宇宙的科學討論和關於它的期刊文章變得突出。[15]
2010年左右,斯蒂芬·M·菲尼等科學家分析了威爾金森微波各向異性探測器(WMAP)的數據,並聲稱發現了證據表明該宇宙在遙遠的過去與其他(平行)宇宙相撞。[16][17][18]然而,對WMAP和普朗克衛星的數據進行更徹底的分析,普朗克衛星的解析度是WMAP的三倍,並沒有發現任何具有統計學意義的證據表明這種泡沫宇宙碰撞。[19][20]此外,沒有證據表明其他宇宙對我們有任何引力。[21][22]
2015年,天體物理學家可能通過回顧大爆炸之後的一段時間,發現了交替或平行宇宙的證據,儘管這仍然是物理學家之間爭論的問題[23]。Ranga-Ram Chary博士在分析了宇宙微波背景後,根據科學家認為存在於早期宇宙中的質子和電子的數量,發現了一個比應有的亮度高4,500倍的信號,事實上,這種特殊的信號——在復合時代原子形成產生的發射線——更符合物質粒子與光子的比例大約是我們自己的65倍的宇宙。有30%的可能性,這個神秘的信號只是噪音,根本不是真正的信號;然而,它也有可能是真實的,並且存在,因為一個平行宇宙將它的一些物質粒子傾倒到我們自己的宇宙中。畢竟,如果在重組過程中將更多的質子和電子添加到我們的宇宙中,就會形成更多的原子。在它們形成過程中會發射更多的光子。所有這些排放產生的簽名線將大大增強。Chary本人明智地持懷疑態度:
Chary還指出[24]:
其他说法
參考資料
- Swain, Frank. . London: New Scientist. 2017: 12. ISBN 9781473658677.
- James, William, The Will to Believe, 1895; and earlier in 1895, as cited in OED's new 2003 entry for "multiverse": "1895 W. JAMES in Internat. Jrnl. Ethics 6 10 Visible nature is all plasticity and indifference, a multiverse, as one might call it, and not a universe."
- Tegmark, Max. . Scientific American. May 2003.
- Tegmark, Max. (PDF). January 23, 2003 [2006-02-07]. (原始内容 (PDF)存档于2006-03-04). (PDF)
- . Physics World. 2019-01-03 [2022-06-22].
- Letzter, Rafi. . Space.com. 2020-06-23 [2022-06-22] (英语).
- Boyle, Latham; Finn, Kieran; Turok, Neil. . Physical Review Letters. 2018-12-20, 121 (25): 251301. Bibcode:2018PhRvL.121y1301B. PMID 30608856. S2CID 58638592. arXiv:1803.08928
 . doi:10.1103/PhysRevLett.121.251301.
. doi:10.1103/PhysRevLett.121.251301. - . Physics World. 2022-05-31 [2022-06-22].
- Cyr-Racine, Francis-Yan; Ge, Fei; Knox, Lloyd. . Physical Review Letters. 2022-05-18, 128 (20): 201301. Bibcode:2022PhRvL.128t1301C. PMID 35657861. S2CID 248904936. arXiv:2107.13000
 . doi:10.1103/PhysRevLett.128.201301.
. doi:10.1103/PhysRevLett.128.201301. - Bedford, Bailey. . Joint Quantum Institute. [2022-06-22] (英语).
- Parhizkar, Alireza; Galitski, Victor. . Physical Review Research. 2022-05-02, 4 (2): L022027. Bibcode:2022PhRvR...4b2027P. S2CID 236965490. arXiv:2108.04252
 . doi:10.1103/PhysRevResearch.4.L022027.
. doi:10.1103/PhysRevResearch.4.L022027. - Parhizkar, Alireza; Galitski, Victor. . 2022. arXiv:2204.06574
 [hep-th].
[hep-th]. - . 中国科学院. 2013-05-23 [2013-05-24]. (原始内容存档于2020-11-15).
- Pathria, R. K. . Nature. 1972-12-01, 240 (5379): 298–299. Bibcode:1972Natur.240..298P. ISSN 0028-0836. S2CID 4282253. doi:10.1038/240298a0.
- Romeo, Jess. . JSTOR Daily. JSTOR. 2022-01-07 [2023-07-15] (美国英语).
- . technologyreview.com. 13 December 2010 [2013-10-12].
- Tegmark, Max; Vilenkin, Alexander. . Scientific American. 19 July 2011 [2013-10-12].
- . Science Daily. sciencedaily.com. 3 August 2011 [2013-10-12].
- Feeney, Stephen M.; et al. . Physical Review D. 2011, 84 (4): 43507. Bibcode:2011PhRvD..84d3507F. S2CID 43793857. arXiv:1012.3667
 . doi:10.1103/PhysRevD.84.043507.
. doi:10.1103/PhysRevD.84.043507. - Feeney; et al. . Physical Review Letters. 2011, 107 (7): 071301. Bibcode:2011PhRvL.107g1301F. PMID 21902380. S2CID 23560957. arXiv:1012.1995
 . doi:10.1103/PhysRevLett.107.071301.. Bousso, Raphael; Harlow, Daniel; Senatore, Leonardo. . Physical Review D. 2015, 91 (8): 083527. Bibcode:2015PhRvD..91h3527B. S2CID 118488797. arXiv:1309.4060
. doi:10.1103/PhysRevLett.107.071301.. Bousso, Raphael; Harlow, Daniel; Senatore, Leonardo. . Physical Review D. 2015, 91 (8): 083527. Bibcode:2015PhRvD..91h3527B. S2CID 118488797. arXiv:1309.4060  . doi:10.1103/PhysRevD.91.083527.
. doi:10.1103/PhysRevD.91.083527. - Collaboration, Planck; Ade, P. A. R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Balbi, A.; Banday, A. J.; Barreiro, R. B.; Battaner, E.; Benabed, K.; Benoit-Levy, A.; Bernard, J. -P.; Bersanelli, M.; Bielewicz, P.; Bikmaev, I.; Bobin, J.; Bock, J. J.; Bonaldi, A.; Bond, J. R.; Borrill, J.; Bouchet, F. R.; Burigana, C.; Butler, R. C.; Cabella, P.; Cardoso, J. -F.; Catalano, A.; Chamballu, A.; et al. . Astronomy & Astrophysics. 2013-03-20, 561: A97. Bibcode:2014A&A...561A..97P. S2CID 2745526. arXiv:1303.5090
 . doi:10.1051/0004-6361/201321299.
. doi:10.1051/0004-6361/201321299. - . New Scientist. 3 April 2013 [2014-03-10].
- Template:Citar web por Doyle Rice, "USA TODAY" (2015)
- . phys.org. por Vanessa Janek, "Universe Today" (2015)
參考文獻
- Bernard Carr, ed. (2007) Universe or Multiverse? Cambridge Univ. Press.
- . Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences. 1985-07-08, 400 (1818) [2022-06-08]. ISSN 0080-4630. doi:10.1098/rspa.1985.0070. (原始内容存档于2022-09-27) (英语).
- Ellis, G. F. R; Kirchner, U.; Stoeger, W. R. . Monthly Notices of the Royal Astronomical Society. 2004-01-21, 347 (3) [2022-06-08]. Bibcode:2004MNRAS.347..921E. ISSN 0035-8711. arXiv:astro-ph/0305292
 . doi:10.1111/j.1365-2966.2004.07261.x. (原始内容存档于2022-08-12) (英语).
. doi:10.1111/j.1365-2966.2004.07261.x. (原始内容存档于2022-08-12) (英语). - Surya-Siddhanta: A Text Book of Hindu Astronomy by Ebenezer Burgess, ed. Phanindralal Gangooly (1989/1997) with a 45-page commentary by P. C. Sengupta (1935).
外部連結
- Aurélien Barrau, "Physics in the Multiverse. (页面存档备份,存于)"
- "Multiple Universes? (页面存档备份,存于)" (in French). Review of Carr (2007).
- Micu, L. . Modern Physics Letters A. 2003-12-28, 18 (40) [2022-06-08]. ISSN 0217-7323. arXiv:astro-ph/0403047
 . doi:10.1142/S0217732303012325. (原始内容存档于2022-01-21) (英语).
. doi:10.1142/S0217732303012325. (原始内容存档于2022-01-21) (英语). - David Deutsch (2001) "The Structure of the Multiverse."
- Max Tegmark, "Parallel universes. Not just a staple of science fiction, other universes are a direct implication of cosmological observations."
- . BBC. [2022-06-08]. (原始内容存档于2022-06-08).
- Michael Price's Everett FAQ.(页面存档备份,存于)
- Jürgen Schmidhuber, "The ensemble of universes describable by constructive mathematics. (页面存档备份,存于)"
- Interview with Tufts cosmologist Alex Vilenkin(页面存档备份,存于) on his new book, "Many Worlds in One: The Search for Other Universes" on the podcast and public radio interview program ThoughtCast.(页面存档备份,存于)
- Joseph Pine II about Multiverse, Presentation at Mobile Monday Amsterdam, 2008
- . BBC Four. [2022-06-08]. (原始内容存档于2022-06-08) (英国英语).
- Benson "平行宇宙"