幾何分佈
在概率论和统计学中,幾何分佈(英語:)指的是以下两种離散型機率分布中的一种:
- 在伯努利試驗中,得到一次成功所需要的試驗次数。的值域是{ 1, 2, 3, ... }
- 在得到第一次成功之前所经历的失败次数。Y的值域是{ 0, 1, 2, 3, ... }
概率質量函數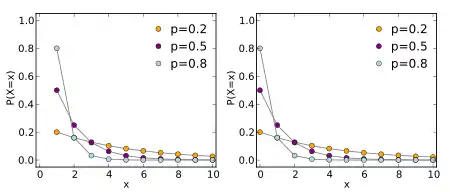 | ||
累積分布函數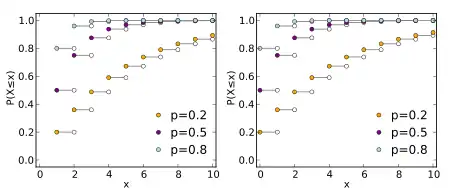 | ||
| 參數 | 成功概率(实) | 成功概率(实) |
|---|---|---|
| 支撑集 | ||
| 概率质量函数 (pmf) | ||
| 累積分布函數 (cdf) | ||
| 期望值 | ||
| 中位數 | (如果是整数,则中位数不唯一) | (如果是整数,则中位数不唯一) |
| 众数 | ||
| 方差 | ||
| 偏度 | ||
| 超值峰度 | ||
| 熵 | ||
| 動差生成函數 (mgf) | , for |
|
| 特征函数 | ||
实际使用中指的是哪一个取决于惯例和使用方便。
这两种分布不应该混淆。前一种形式(的分布)经常被称作shifted geometric distribution;但是,为了避免歧义,最好明确地说明取值范围。
如果每次试验的成功概率是,那么次试验中,第次才得到成功的概率是,
其中.
上式描述的是取得一次成功所需要的试验次数。而另一种形式,也就是第一次成功之前所失败的次数,可以写为,
其中
两种情况产生的序列都是几何数列。这是几何分布的名字来源。
比如,假设不停地掷骰子,直到得到1。投掷次数是随机分布的,取值范围是无穷集合{ 1, 2, 3, ... },并且是一个的几何分布。
性质
呈几何分布的随机变量X的期望值是1/p,方差是 (1-p)/p2:
幾何分布具有非記憶性的性質(Memoryless Property,又稱遺失記憶性)
這表示如果一個隨機變數呈幾何分布,它的條件機率遵循:
- s, t ∈ℕ.
记号
若随机变量服从参数为的几何分布,则记为.
用途
在重复多次的伯努利試驗中,试验进行到某种结果出现第一次为止,此时的试验总次数服从几何分布,如:射击,首次击中目标时的次数。
參見
- 機率分布
- 超几何分布
- 負二項分布
- 指數分布
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.