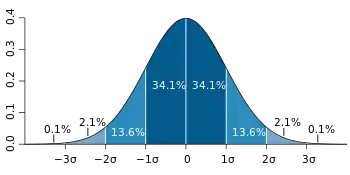
标准误差
概述
标准误差针对样本统计量而言,是某个样本统计量的标准差。当谈及标准误差时,一般须指明对应的样本统计量才有意义。以下以样本均值(样本均值是一种样本统计量)作为例子:
例如, 样本均值是总体均值的无偏估计。但是,来自同一总量的不同样本可能有不同的均值。
于是,假设可以从总体中随机选取无限的大小相同的样本,那每个样本都可以有一个样本均值。依此法可以得到一个由无限多样本均值组成的总体,该总体的标准差即为标准误差。
在很多实际应用中,标准差的真正值通常是未知的。因此,标准误这个术语通常运用于代表这一未知量的估计。在这些情况下,需要清楚业已完成的和尝试去解决的标准误差仅仅可能是一个估量。然而,这通行上不太可能:人们可能往往采取更好的估量方法,而避免使用标准误,例如采用最大似然或更形式化的方法去测定信賴區間。第一个众所周知的方法是在适当条件下可以采用学生t-分布为一个估量平均值提供置信区间。在其他情况下,标准差可以有效地利用于提供一个不确定性空间的示值,但其正式或半正式使用是提供置信区间或测试,并要求样本总量必须足够大。其总量大小取决于具体的数量分析[2]。
平均值标准误差
「样本均值的估計标准误差」,簡稱平均值标准误差(),或平均数标准误差。必須記得在簡稱的背後總是意指「樣本的」。
如果已知总體的標準差(σ),那麼抽取無限多份大小為 n 的樣本,每個樣本各有一個平均值,所有這個大小的樣本之平均值的標準差可證明為(注意!不是一份樣本裡觀察值的標準差(那是下面公式裡的)):
但由於通常σ為未知,此時可以用研究中取得樣本的標準差 (s) 來估計:
其中,s为样本的标准差,n为样本数量(大小)。
名詞比較:
- :樣本平均值的標準「差」 (standard deviation of sample mean)
- :「樣本的」標準差 (standard deviation of sample)
- :樣本平均值的標準「誤」 (standard error of sample mean)。
注意:
假设与运用
如果数据集服从正态分布,其正态分布函数的分位数、样本平均数和标准差都可以用来计算合适的平均数信賴區間。
以下公式表示在大于或小于95%的置信区间中, 等于样本平均数时,S 等于样本平均数的标准差,1.96 则为服从正态分布的第 0.975百分位数值。
- 95% 置信区间的上限 = + (S ×1.96) ,
- 95% 置信区间的下限 = - (S ×1.96) .
特殊情况下,样本统计(比如样本平均数)的标准误是一个有偏誤的估计标准。换句话说,标准误是一个样本统计的样本分布的标准差。这一标准误的符号可以是任何、、之一。
标准误提供一系列在证明数值不确定性的简单方法,并通常用于:
有限总体校正
鉴于对上述标准误差的公式,假设样本量远小于总量规模,所以总量可以被视为足够大。当取样比例较大(大约为5%或以上)时,对标准误的估计必须用“有限总体校正”()[6]:
| FPC() | FPC() |
|---|---|
| 樣本元素為不可重復組合 | 樣本元素為可重復組合 |
| 所有可能樣本的數目 = | 所有可能樣本的數目 = |
该公式以考虑到增加所获得的采样精度,以接近的人口较大比例。有限总体校正的意义在于:如果样本大小 n 等于总量大小 N 时,有限总体校正数值为零。
样本相关性校正
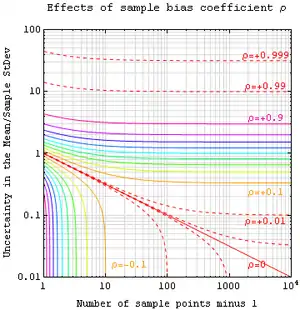
如果实测量 A 的数值不具有统计意义上的独立性,但是其仍然可以从已知的参数空间 x 中获取。那么一个误差的无偏估计可以通过以下方程获得:
其中,样本偏差系数 ρ 为自相关系数 ρij (-1到1之间的数量)的平均值。
相对标准误差
相对标准误差()仅仅是标准误除以平均值的一种百分比表述。例如,制作两份家庭收入调查,其平均值为50000美元。如果一个调查的标准误有10000美元,而另一个则为5000美元,其相对标准误差分别为20%和10%。直观地说,拥有较低标准误差的调查看起来更为可靠。事实上,由于制作数据机构通常预设可信度标准,以使得其统计数据必须满足此前公布的内容。譬如,美国国家卫生统计中心通常不会报告其数据相对标准误差超过30%的估计。
参考文献
- Everitt, B.S. (2003) The Cambridge Dictionary of Statistics, CUP. ISBN 0-521-81099-X
- Isserlis, L. . Journal of the Royal Statistical Society. 1918, 81 (1): 75–81 [2010-03-28]. (原始内容存档于2021-03-08).
- Kenney, J. and Keeping, E.S. (1963) Mathematics of Statistics, van Nostrand, p. 187
- Zwillinger D. (1995), Standard Mathematical Tables and Formulae, Chapman&Hall/CRC. ISBN 0-8493-2479-3 p. 626
- Gurland, J; Tripathi RC. . American Statistician. 1971, 25 (4): 30–32.
- Isserlis (1981,equation (1))