累积分布函数
累积分布函数(英語:,CDF)或概率分布函数,简称分布函数,是概率密度函數的积分,能完整描述一個實随机变量的概率分佈。
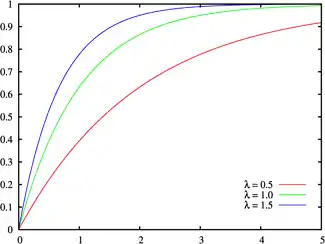
指数分布的累积分布函数
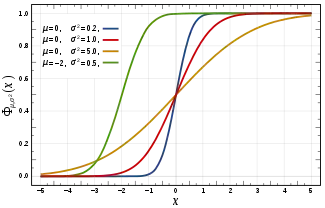
正态分布的累积分布函数
在標量連續分佈的情況下,它給出了從負無窮到的概率密度函數下的面積。 累積分佈函數也用於指定多元隨機變量的分佈。
定義
對於所有實數值的随机变量 ,累积分布函数定義如下[1]:p. 77:
| () |
其中右侧表示随机变量取值小于或等于的概率。
對於位于半闭区间 的概率,其中,因此定義是[1]:p. 84:
| () |
在上面的定義中,“小於或等於”符號“≤”是一種約定,不是普遍使用的(例如匈牙利文獻使用“<”),但這種區別對於離散分佈很重要。二項式分布和泊松分布的表格的正確使用取決於此約定。此外,像數學家保羅·皮埃爾·萊維(Paul Lévy)的特徵函數反演公式等重要公式也依賴於“小於或等於”公式。
反函数
若累积分布函数 是连续的严格增函数,则存在其反函数。累积分布函数的反函数可以用来生成服从该随机分布的随机变量。设若是概率分布的累积分布函数,并存在反函数。若是区间上均匀分布的随机变量,则服从分布。
互补累积分布函数
互补累積分布函数(complementary cumulative distribution function、CCDF),是对连续函数,所有大于的值,其出现概率的和。
參見
- 機率密度函數
- 機率質量函數
參考
- Park, Kun Il. . Springer. 2018. ISBN 978-3-319-68074-3.
- 《概率論與數理統計教程》茆詩松 程依明 濮曉龍
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.