二項式分布
在概率论和统计学中,二项分布(英語:)是一种离散概率分布,描述在进行独立随机试验时,每次试验都有相同概率“成功”的情况下,获得成功的总次数。掷硬币十次出现五次正面的概率、产品合格率时抽出一百件样本没有发现一件次品的概率等等,都可以由二项分布给出。
|
质量函數 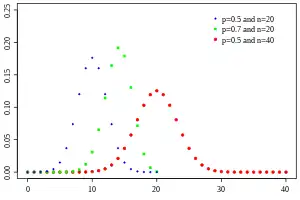 | |||
|
累積分布函數 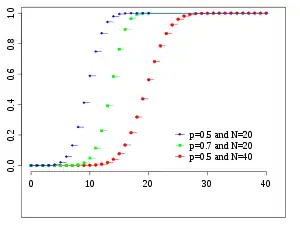 | |||
| 记号 | |||
|---|---|---|---|
|
| |||
| 值域 | |||
| 累積分布函數 | |||
| 期望值 | |||
| 中位數 | 或 | ||
| 眾數 | |||
| 偏度 | |||
| 峰度 | |||
| 熵 | |||
| 特徵函数 | |||
只有“成功”和“失败”两种可能结果,每次重复时成功概率不变的独立随机试验称作伯努利试验,例如上述的掷硬币出现正面或反面、对产品进行抽样检查时抽到正品或次品。伯努利试验作为理论模型,其前提在现实中无法完全得到满足,比如生产线会磨损,因此每件产品合格的概率并非固定[1]。尽管如此,二项分布给出的概率通常足以用于提供有用的推断;即使在已知前提没有满足的场合,二项分布也能用于参考和比较。二项分布的应用出现在遗传学、质量控制等领域之中。[2]
历史
二项分布是最早得到研究的概率分布之一[6]。丹麦统计学家安德斯·哈爾德认为其历史可以追溯至布莱兹·帕斯卡与皮埃尔·德·费马于1654年对点数分配问题的讨论:两名玩家赢得每局游戏的机会相同,赢得一定局数的胜者可获得奖金,但比赛仅进行了数局,尚未分出胜负就被迫中断,则奖金该如何分配?帕斯卡认为,奖金的分配应当基于玩家距离胜利所差的局数:若一名玩家还需局获胜,另一名玩家还需局获胜,则应考虑在局比赛的种结果中,两名玩家分别在多少种情况中获胜。两人的讨论限于这一问题本身,并未推导出二项分布的概率,但这一解法可被视作基于参数的二项分布。[7]
对二项分布概率的推导为雅各布·伯努利于《猜度术》中作出。该著作在他去世后,于1713年得到出版,被视作概率论的奠基性作品。伯努利还在其中首次给出了弱大数定律的严格证明[8][9]。对二项分布的正态近似则是由亞伯拉罕·棣莫弗发现,这一工作于1733年完成,于1738年出版在其著作《机遇论》的第二版中。[10]
性质
矩母函数为
特征函数为
参数的二项分布称作伯努利分布[3]。多项分布是二项分布的拓展,描述重复进行不限于两种结果、可能有多种可能结果的随机试验时的概率[12]。二项分布本身是超几何分布的极限形式。[13]
二项分布的和
若两个随机变量独立,分别服从参数为和的二项分布,则即是在次独立伯努利试验中取得成功的次数,所以服从参数为的二项分布。这一结论亦可通过将两者的概率母函数相乘而得出。在条件之下,随机变量的条件概率分布是参数为的超几何分布。[14]
近似
参数估计
点估计
通常参数为已知。假设随机变量服从二项分布,其参数未知。若观测到的值为,采用矩估计和最大似然估计对参数的估计量均为,这一估计量为无偏的。[26]
参数的贝叶斯估计量取决于使用的先验分布。若使用连续型均匀分布作为先验分布,即假设和之间任意等长的区间包含的概率都相同,则后验均值估计量为
这被称作拉普拉斯–贝叶斯估计量,曾被皮埃尔-西蒙·拉普拉斯用于估计在太阳连续升起天之后,太阳明天还会升起的概率。由于人类知道太阳在过去五千年,即1,826,213天都正常升起,拉普拉斯愿意以1,826,214比1的赔率赌太阳明天继续升起。[27]
若使用参数为的贝塔分布作为先验分布,则后验均值估计量为
采用贝塔分布作为先验分布时,后验分布亦是贝塔分布,即贝塔分布为二项分布的共轭先验。[28]
注释
- Feller 1968,第146–147頁.
- Johnson, Kemp & Kotz 2005,第135–136頁.
- Johnson, Kemp & Kotz 2005,第108頁.
- Feller 1968,第34頁.
- Feller 1968,第147–150頁.
- Johnson, Kemp & Kotz 2005,第109頁.
- Hald 2003,第54–63頁.
- Hald 2003,第223–228頁.
- Stigler 1986,第62–70頁.
- Stigler 1986,第70–85頁.
- Johnson, Kemp & Kotz 2005,第109–112頁.
- Feller 1968,第167–169頁.
- Johnson, Kemp & Kotz 2005,第140頁.
- Johnson, Kemp & Kotz 2005,第115頁.
- Johnson, Kemp & Kotz 2005,第112頁.
- Kaas & Buhrman 1980.
- Hamza 1995.
- Johnson, Kemp & Kotz 2005,第119頁.
- Johnson, Kemp & Kotz 2005,第110頁.
- Feller 1968,第182–185頁.
- Feller 1968,第185–186頁.
- Schader & Schmid 1989.
- Johnson, Kemp & Kotz 2005,第116–117頁.
- Feller 1968,第153–154頁.
- Sheu 1984.
- Johnson, Kemp & Kotz 2005,第126頁.
- Feller 1968,第123–124頁.
- Chew 1971.
- Johnson, Kemp & Kotz 2005,第130–131頁.
- Johnson, Kemp & Kotz 2005,第132頁.
- Blyth 1986.
参考文献
- Blyth, C. R. . Journal of the American Statistical Association. 1986, 81: 843–855. doi:10.1080/01621459.1986.10478343 (英语).
- Chew, V. . The American Statistician. 1971, 25 (5): 47–50. doi:10.1080/00031305.1971.10477305 (英语).
- Feller, W. . Wiley. 1968. ISBN 0-471-25708-7 (英语).
- Hald, A. . Wiley. 2003. ISBN 0-471-47129-1 (英语).
- Hamza, K. . Statistics and Probability Letters. 1995, 23: 21–25. doi:10.1016/0167-7152(94)00090-U (英语).
- Johnson, N. L.; Kemp, A. W.; Kotz, S. . Wiley. 2005. ISBN 0-471-27246-9 (英语).
- Kaas, R.; Buhrman, J. M. . Statistica Neerlandica. 1980, 34 (1): 13–18. doi:10.1111/j.1467-9574.1980.tb00681.x (英语).
- Schader, M.; Schmid, F. . The American Statistician. 1989, 43 (1): 23–24. doi:10.1080/00031305.1989.10475601 (英语).
- Sheu, S. S. . The American Statistician. 1984, 38 (3): 206–207. doi:10.1080/00031305.1984.10483202 (英语).
- Stigler, S. M. . Harvard University Press. 1986. ISBN 0-674-40340-1 (英语).
