歐拉-馬斯刻若尼常數
歐拉-馬斯刻若尼常數是一个数学常数,定义为调和级数与自然对数的差值:
| 歐拉-馬斯刻若尼常數 | |
|---|---|
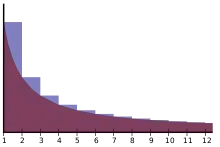 藍色區域的面積收斂到歐拉常數 | |
| 識別 | |
| 符號 | |
| 位數數列編號 | |
| 性質 | |
| 定義 | |
| 連分數 | [0; 1, 1, 2, 1, 2, 1, 4, 3, 13, 5, 1, 1, 8, 1, 2, 4, 1, 1, 40, ...] |
| 表示方式 | |
| 值 | 0.57721566490153... |
| 無窮級數 | |
| 二进制 | 0.100100111100010001100111… |
| 十进制 | 0.577215664901532860606512… |
| 十六进制 | 0.93C467E37DB0C7A4D1BE3F81… |
它的近似值为[1],
歐拉-馬斯刻若尼常數主要应用于数论。
历史
该常数最先由瑞士数学家莱昂哈德·欧拉在1735年发表的文章De Progressionibus harmonicus observationes中定义。欧拉曾经使用作为它的符号,并计算出了它的前6位小数。1761年他又将该值计算到了16位小数。1790年,意大利数学家洛倫佐·馬斯凱羅尼引入了作为这个常数的符号,并将该常数计算到小数点后32位。但后来的计算显示他在第20位的时候出现了错误。
已知位数
| 日期 | 位数 | 计算者 |
|---|---|---|
| 1734年 | 5 | 莱昂哈德·欧拉 |
| 1736年 | 15 | 莱昂哈德·欧拉 |
| 1790年 | 19 | 洛倫佐·馬斯凱羅尼 |
| 1809年 | 24 | Johann G. von Soldner |
| 1812年 | 40 | F.B.G. Nicolai |
| 1861年 | 41 | Oettinger |
| 1869年 | 59 | William Shanks |
| 1871年 | 110 | William Shanks |
| 1878年 | 263 | 约翰·柯西·亚当斯 |
| 1962年 | 1,271 | 高德纳 |
| 1962年 | 3,566 | D.W. Sweeney |
| 1977年 | 20,700 | Richard P. Brent |
| 1980年 | 30,100 | Richard P. Brent和埃德温·麦克米伦 |
| 1993年 | 172,000 | Jonathan Borwein |
| 1997年 | 1,000,000 | Thomas Papanikolaou |
| 1998年12月 | 7,286,255 | Xavier Gourdon |
| 1999年10月 | 108,000,000 | Xavier Gourdon和Patrick Demichel |
| 2006年7月16日 | 2,000,000,000 | Shigeru Kondo和Steve Pagliarulo |
| 2006年12月8日 | 116,580,041 | Alexander J. Yee |
| 2007年7月15日 | 5,000,000,000 | Shigeru Kondo和Steve Pagliarulo |
| 2008年1月1日 | 1,001,262,777 | Richard B. Kreckel |
| 2008年1月3日 | 131,151,000 | Nicholas D. Farrer |
| 2008年6月30日 | 10,000,000,000 | Shigeru Kondo和Steve Pagliarulo |
| 2009年1月18日 | 14,922,244,771 | Alexander J. Yee和Raymond Chan |
| 2009年3月13日 | 29,844,489,545 | Alexander J. Yee和Raymond Chan |
| 2013年 | 119,377,958,182 | Alexander J. Yee |
| 2016年 | 160,000,000,000 | Peter Trueb |
| 2016年 | 250,000,000,000 | Ron Watkins |
| 2017年 | 477,511,832,674 | Ron Watkins |
| 2020年 | 600,000,000,100 | Seungmin Kim和Ian Cutress |
相关证明
- 的证明:
首先根据放缩法()容易知道,,以及。因此存在并有限。
而
所以
(单调收敛定理)
前面的放缩法主要是证明了
- 是单调递减并下有界限(0),所有极限存在。放缩法的结论需要使用ln(1+x)和ln(1-x)的泰勒级数展开进行证明。
參考文獻
- A001620 oeis.org [2014-7-17]
- Havil 2003 p 97.
- Borwein, Jonathan M., David M. Bradley, Richard E. Crandall. (PDF). Journal of Computational and Applied Mathematics. 2000, 121: 11 [2014-07-17]. doi:10.1016/s0377-0427(00)00336-8. (原始内容 (PDF)存档于2006-09-25). Derives γ as sums over Riemann zeta functions.
- Gourdon, Xavier, and Sebah, P. (2002) "Collection of formulas for Euler's constant, γ. (页面存档备份,存于)"
- Gourdon, Xavier, and Sebah, P. (2004) "The Euler constant: γ. (页面存档备份,存于)"
- Donald Knuth (1997) The Art of Computer Programming, Vol. 1, 3rd ed. Addison-Wesley. ISBN 978-0-201-89683-1
- Krämer, Stefan (2005) Die Eulersche Konstante γ und verwandte Zahlen. Diplomarbeit, Universität Göttingen.
- Sondow, Jonathan (1998) "An antisymmetric formula for Euler's constant," Mathematics Magazine 71: 219-220.
- Sondow, Jonathan (2002) "A hypergeometric approach, via linear forms involving logarithms, to irrationality criteria for Euler's constant." With an Appendix by Sergey Zlobin, Mathematica Slovaca 59: 307-314.
- Sondow, Jonathan. . 2003. arXiv:math.CA/0306008
 .
. - Sondow, Jonathan (2003a) "Criteria for irrationality of Euler's constant," Proceedings of the American Mathematical Society 131: 3335-3344.
- Sondow, Jonathan (2005) "Double integrals for Euler's constant and ln 4/π and an analog of Hadjicostas's formula," American Mathematical Monthly 112: 61-65.
- Sondow, Jonathan (2005) "New Vacca-type rational series for Euler's constant and its 'alternating' analog ln 4/π."
- Sondow, Jonathan; Zudilin, Wadim. . 2006. arXiv:math.NT/0304021
 . Ramanujan Journal 12: 225-244.
. Ramanujan Journal 12: 225-244. - G. Vacca (1926), "Nuova serie per la costante di Eulero, C = 0,577…". Rendiconti, Accademia Nazionale dei Lincei, Roma, Classe di Scienze Fisiche, Matematiche e Naturali (6) 3, 19–20.
- James Whitbread Lee Glaisher (1872), "On the history of Euler's constant". Messenger of Mathematics. New Series, vol.1, p. 25-30, JFM 03.0130.01
- Carl Anton Bretschneider (1837). "Theoriae logarithmi integralis lineamenta nova". Crelle Journal, vol.17, p. 257-285 (submitted 1835)
- Lorenzo Mascheroni (1790). "Adnotationes ad calculum integralem Euleri, in quibus nonnulla problemata ab Eulero proposita resolvuntur". Galeati, Ticini.
- Lorenzo Mascheroni (1792). "Adnotationes ad calculum integralem Euleri. In quibus nonnullae formulae ab Eulero propositae evolvuntur". Galeati, Ticini. Both online at: http://books.google.de/books?id=XkgDAAAAQAAJ (页面存档备份,存于)
- Havil, Julian. . Princeton University Press. 2003. ISBN 0-691-09983-9.
- Karatsuba, E. A. . Probl. Inf. Transm. 1991, 27 (44): 339–360.
- E.A. Karatsuba, On the computation of the Euler constant γ, J. of Numerical Algorithms Vol.24, No.1-2, pp. 83–97 (2000)
- M. Lerch, Expressions nouvelles de la constante d'Euler. Sitzungsberichte der Königlich Böhmischen Gesellschaft der Wissenschaften 42, 5 p. (1897)
- Lagarias, Jeffrey C. . arXiv:1303.1856
 ., Bulletin of the American Mathematical Society 50 (4): 527-628 (2013)
., Bulletin of the American Mathematical Society 50 (4): 527-628 (2013)
外部連結
- 埃里克·韦斯坦因. . MathWorld.
- Krämer, Stefan "Euler's Constant γ=0.577... Its Mathematics and History."
- Jonathan Sondow.
- Fast Algorithms and the FEE Method (页面存档备份,存于), E.A. Karatsuba (2005)
- Further formulae which make use of the constant: Gourdon and Sebah (2004). (页面存档备份,存于)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.