深度学习
深度学习(英語:)是机器学习的分支,是一種以人工神經網路為架構,對資料進行表徵學習的算法。[1][2][3][4][5] 深度学习中的形容词“深度”是指在网络中使用多层。 早期的工作表明,线性感知器不能成为通用分类器,但具有非多项式激活函数和一个无限宽度隐藏层的网络可以成为通用分类器。
| 机器学习与 |
|---|
 |
| 人工智能系列内容 |
|---|
深度学习是机器学习中一种基于对数据进行表征学习的算法。观测值(例如一幅图像)可以使用多种方式来表示,如每个像素强度值的向量,或者更抽象地表示成一系列边、特定形状的区域等。而使用某些特定的表示方法更容易从实例中学习任务(例如,人脸识别或面部表情识别[6])。深度学习的好处是用非监督式或半监督式的特征学习和分层特征提取高效算法来替代手工获取特征。[7]
表征学习的目标是寻求更好的表示方法并建立更好的模型来从大规模未标记数据中学习这些表示方法。表示方法来自神经科学,并松散地建立在類似神经系统中的信息处理和对通信模式的理解上,如神经编码,试图定义拉動神经元的反应之间的关系以及大脑中的神经元的电活动之间的关系。[8]
至今已有數种深度学习框架,如深度神经网络、卷积神经网络和深度置信网络和循环神经网络已被应用在计算机视觉、语音识别、自然语言处理、音频识别与生物信息学等领域并取得了极好的效果。
简介
深度学习框架,尤其是基于人工神经网络的框架可以追溯到1980年福岛邦彦提出的新认知机[11],而人工神经网络的历史更为久远。1989年,扬·勒丘恩(Yann LeCun)等人开始将1974年提出的标准反向传播算法[12]应用于深度神经网络,这一网络被用于手写邮政编码识别。尽管算法可以成功执行,但计算代价非常巨大,神经网络的训练时间达到了3天,因而无法投入实际使用[13]。许多因素导致了这一缓慢的训练过程,其中一种是由于尔根·施密德胡伯的学生赛普·霍克赖特于1991年提出的梯度消失问题[14][15]。
最早的进行一般自然杂乱图像中自然物体识别的深度学习网络是翁巨扬(Juyang Weng)等在1991和1992发表的生长网(Cresceptron)[16][17][18]。它也是第一个提出了后来很多实验广泛采用的一个方法:现在称为最大汇集(max-pooling)以用于处理大物体的变形等问题。生长网不仅直接从杂乱自然场景中学习老师指定的一般物体,还用网络反向分析的方法把图像内被识别了的物体从背景图像中分割出来。
2007年前后,杰弗里·辛顿和鲁斯兰·萨拉赫丁诺夫(Ruslan Salakhutdinov)提出了一种在前馈神经网络中进行有效训练的算法。这一算法将网络中的每一层视为无监督的受限玻尔兹曼机,再使用有监督的反向传播算法进行调优[19]。在此之前的1992年,在更为普遍的情形下,施密德胡伯也曾在循环神经网络上提出一种类似的训练方法,并在实验中证明这一训练方法能够有效提高有监督学习的执行速度[20][21].
自深度学习出现以来,它已成为很多领域,尤其是在计算机视觉和语音识别中,成为各种领先系统的一部分。在通用的用于检验的数据集,例如语音识别中的TIMIT和图像识别中的ImageNet, Cifar10上的实验证明,深度学习能够提高识别的精度。与此同时,神经网络也受到了其他更加简单归类模型的挑战,支持向量机等模型在20世纪90年代到21世纪初成为过流行的机器学习算法。
硬件的进步也是深度学习重新获得关注的重要因素。高性能图形处理器的出现极大地提高了数值和矩阵运算的速度,使得机器学习算法的运行时间得到了显著的缩短[22][23]。
由于脑科学方面的大量研究已表明人脑网络不是一个级联的结构,深度学习网络在2001年后正逐渐被更有潜力的基于脑模型的网络[24][25]所替代。
基本概念
深度学习的基础是机器学习中的分散表示(distributed representation)。分散表示假定观测值是由不同因子相互作用生成。在此基础上,深度学习进一步假定这一相互作用的过程可分为多个层次,代表对观测值的多层抽象。不同的层数和层的规模可用于不同程度的抽象[3]。
深度学习运用了这分层次抽象的思想,更高层次的概念从低层次的概念学习得到。这一分层结构常常使用贪婪算法逐层构建而成,并从中选取有助于机器学习的更有效的特征[3]。
不少深度学习算法都以无监督学习的形式出现,因而这些算法能被应用于其他算法无法企及的无标签数据,这一类数据比有标签数据更丰富,也更容易获得。这一点也为深度学习赢得了重要的优势[3]。
人工神经网络下的深度学习
一部分最成功的深度学习方法涉及到对人工神经网络的运用。人工神经网络受到了1959年由诺贝尔奖得主大卫·休伯尔(David H. Hubel)和托斯坦·威泽尔(Torsten Wiesel)提出的理论启发。休伯尔和威泽尔发现,在大脑的初级视觉皮层中存在两种细胞:简单细胞和复杂细胞,这两种细胞承担不同层次的视觉感知功能。受此启发,许多神经网络模型也被设计为不同节点之间的分层模型[26]。
福岛邦彦提出的新认知机引入了使用无监督学习训练的卷积神经网络。扬·勒丘恩将有监督的反向传播算法应用于这一架构[27]。事实上,从反向传播算法自20世纪70年代提出以来,不少研究者都曾试图将其应用于训练有监督的深度神经网络,但最初的尝试大都失败。赛普·霍克赖特在其博士论文中将失败的原因归结为梯度消失,这一现象同时在深度前馈神经网络和循环神经网络中出现,后者的训练过程类似深度网络。在分层训练的过程中,本应用于修正模型参数的误差随着层数的增加指数递减,这导致了模型训练的效率低下[28][29]。
为了解决这一问题,研究者们提出了一些不同的方法。于尔根·施密德胡伯于1992年提出多层级网络,利用无监督学习训练深度神经网络的每一层,再使用反向传播算法进行调优。在这一模型中,神经网络中的每一层都代表观测变量的一种压缩表示,这一表示也被传递到下一层网络[20]。
另一种方法是赛普·霍克赖特和于尔根·施密德胡伯提出的長短期記憶神經網路(LSTM)[30]。2009年,在ICDAR 2009举办的连笔手写识别竞赛中,在没有任何先验知识的情况下,深度多维长短期记忆神经网络取得了其中三场比赛的胜利[31][32]。
斯文·贝克提出了在训练时只依赖梯度符号的神经抽象金字塔模型,用以解决图像重建和人脸定位的问题[33]。
其他方法同样采用了无监督预训练来构建神经网络,用以发现有效的特征,此后再采用有监督的反向传播以区分有标签数据。杰弗里·辛顿等人于2006年提出的深度模型提出了使用多层隐变量学习高层表示的方法。这一方法使用斯摩棱斯基于1986年提出的受限玻尔兹曼机[34]对每一个包含高层特征的层进行建模。模型保证了数据的对数似然下界随着层数的提升而递增。当足够多的层数被学习完毕,这一深层结构成为一个生成模型,可以通过自上而下的采样重构整个数据集[35]。辛顿声称这一模型在高维结构化数据上能够有效地提取特征[36]。
吴恩达和杰夫·迪恩领导的谷歌大脑团队创建了一个仅通过YouTube视频学习高层概念(例如猫)的神经网络[37] [38]。
其他方法依赖了现代电子计算机的强大计算能力,尤其是GPU。2010年,在于尔根·施密德胡伯位于瑞士人工智能实验室IDSIA的研究组中,丹·奇雷尚(Dan Ciresan)和他的同事展示了利用GPU直接执行反向传播算法而忽视梯度消失问题的存在。这一方法在扬·勒丘恩等人给出的手写识别MNIST数据集上战胜了已有的其他方法[22]。
截止2011年,前馈神经网络深度学习中最新的方法是交替使用卷积层(convolutional layers)和最大值池化层(max-pooling layers)并加入单纯的分类层作为顶端。训练过程也无需引入无监督的预训练[39][40]。从2011年起,这一方法的GPU实现[39]多次赢得了各类模式识别竞赛的胜利,包括IJCNN 2011交通标志识别竞赛[41]和其他比赛。
这些深度学习算法也是最先在某些识别任务上达到和人类表现具备同等竞争力的算法[42]。
深度学习结构
通常将具有两层或两层以上隐藏层的神经网络叫做深度神经网络。与浅层神经网络类似,深度神经网络也能够为复杂非线性系统提供建模,但多出的层次为模型提供了更高的抽象层次,因而提高了模型的能力。深度神经网络通常都是前馈神经网络,但也有语言建模等方面的研究将其拓展到循环神经网络[43]。卷积深度神经网络(Convolutional Neural Networks, CNN)在计算机视觉领域得到了成功的应用[44]。此后,卷积神经网络也作为听觉模型被使用在自动语音识别领域,较以往的方法获得了更优的结果[45]。
深度神经网络
深度神经网络(Deep Neural Networks, DNN)是一种判别模型,可以使用反向传播算法进行训练。权重更新可以使用下式进行随机梯度下降法求解:
其中,为学习率,为代价函数。这一函数的选择与学习的类型(例如监督学习、无监督学习、增强学习)以及激活函数相关。例如,为了在一个多分类问题上进行监督学习,通常的选择是使用ReLU作为激活函数,而使用交叉熵作为代价函数。Softmax函数定义为,其中代表类别的概率,而和分别代表对单元和的输入。交叉熵定义为,其中代表输出单元的目标概率,代表应用了激活函数后对单元的概率输出[46]。
深度神经网络的问题
与其他神经网络模型类似,如果仅仅是简单地训练,深度神经网络可能会存在很多问题。常见的两类问题是过拟合和过长的运算时间。
深度神经网络很容易产生过拟合现象,因为增加的抽象层使得模型能够对训练数据中较为罕见的依赖关系进行建模。对此,权重递减(正规化)或者稀疏(-正规化)等方法可以利用在训练过程中以减小过拟合现象[47]。另一种较晚用于深度神经网络训练的正规化方法是丢弃法("dropout" regularization),即在训练中随机丢弃一部分隐层单元来避免对较为罕见的依赖进行建模[48]。目前比較廣泛使用的是批归一化(Batch Normalization,BN) , 其本質上是在訓練過程加入噪音 , 從而讓模型得到更好的魯棒性 , 其特性令超深神經網路可以更好的訓練。
反向传播算法和梯度下降法由于其实现简单,与其他方法相比能够收敛到更好的局部最优值而成为神经网络训练的通行方法。但是,这些方法的计算代价很高,尤其是在训练深度神经网络时,因为深度神经网络的规模(即层数和每层的节点数)、学习率、初始权重等众多参数都需要考虑。扫描所有参数由于时间代价的原因并不可行,因而小批量训练(mini-batching),即将多个训练样本组合进行训练而不是每次只使用一个样本进行训练,被用于加速模型训练[49]。而最显著地速度提升来自GPU,因为矩阵和向量计算非常适合使用GPU实现。但使用大规模集群进行深度神经网络训练仍然存在困难,因而深度神经网络在训练并行化方面仍有提升的空间。
深度置信网络
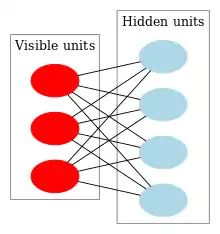
深度置信网络(deep belief networks,DBN)是一种包含多层隐单元的概率生成模型,可被视为多层简单学习模型组合而成的複合模型[50]。
深度置信网络可以作为深度神经网络的预训练部分,并为网络提供初始权重,再使用反向传播或者其它判定算法作为调优的手段。这在训练数据较为缺乏时很有价值,因为不恰当的初始化权重会显著影响最终模型的性能,而预训练获得的权重在权值空间中比随机权重更接近最优的权重。这不仅提升了模型的性能,也加快了调优阶段的收敛速度[51]。
深度置信网络中的每一层都是典型的受限玻尔兹曼机(restricted Boltzmann machine,RBM),可以使用高效的无监督逐层训练方法进行训练。受限玻尔兹曼机是一种无向的基于能量的生成模型,包含一个输入层和一个隐层。图中对的边仅在输入层和隐层之间存在,而输入层节点内部和隐层节点内部则不存在边。单层RBM的训练方法最初由杰弗里·辛顿在训练“专家乘积”中提出,被称为对比分歧(contrast divergence, CD)。对比分歧提供了一种对最大似然的近似,被理想地用于学习受限玻尔兹曼机的权重[49]。当单层RBM被训练完毕后,另一层RBM可被堆叠在已经训练完成的RBM上,形成一个多层模型。每次堆叠时,原有的多层网络输入层被初始化为训练样本,权重为先前训练得到的权重,该网络的输出作为新增RBM的输入,新的RBM重复先前的单层训练过程,整个过程可以持续进行,直到达到某个期望中的终止条件[2]。
尽管对比分歧对最大似然的近似十分粗略(对比分歧并不在任何函数的梯度方向上),但经验结果证实该方法是训练深度结构的一种有效的方法[49]。
卷积神经网络
卷积神经网络(convolutional neural networks,CNN)由一个或多个卷积层和顶端的全连通层(对应经典的神经网络)组成,同时也包括关联权重和池化层(pooling layer)。这一结构使得卷积神经网络能够利用输入数据的二维结构。与其他深度学习结构相比,卷积神经网络在图像和语音识别方面能够给出更优的结果。这一模型也可以使用反向传播算法进行训练。相比较其他深度、前馈神经网络,卷积神经网络需要估计的参数更少,使之成为一种颇具吸引力的深度学习结构[52]。
卷积深度置信网络
卷积深度置信网络(convolutional deep belief networks,CDBN)是深度学习领域较新的分支。在结构上,卷积深度置信网络与卷积神经网络在结构上相似。因此,与卷积神经网络类似,卷积深度置信网络也具备利用图像二维结构的能力,与此同时,卷积深度信念网络也拥有深度置信网络的预训练优势。卷积深度置信网络提供了一种能被用于信号和图像处理任务的通用结构,也能够使用类似深度置信网络的训练方法进行训练[53]。
深度学习与神经科学
计算机领域中的深度学习与20世纪90年代由认知神经科学研究者提出的大脑发育理论(尤其是皮层发育理论)密切相关[57]。对这一理论最容易理解的是杰弗里·艾尔曼于1996年出版的专著《对天赋的再思考》(Rethinking Innateness)[58](参见斯拉格和约翰逊[59]以及奎兹和赛杰诺维斯基[60]的表述)。由于这些理论给出了实际的神经计算模型,因而它们是纯计算驱动的深度学习模型的技术先驱。这些理论指出,大脑中的神经元组成了不同的层次,这些层次相互连接,形成一个过滤体系。在这些层次中,每层神经元在其所处的环境中获取一部分信息,经过处理后向更深的层级传递。这与后来的单纯与计算相关的深度神经网络模型相似。这一过程的结果是一个与环境相协调的自组织的堆栈式的转换器。正如1995年在《纽约时报》上刊登的那样,“……婴儿的大脑似乎受到所谓‘营养因素’的影响而进行着自我组织……大脑的不同区域依次相连,不同层次的脑组织依照一定的先后顺序发育成熟,直至整个大脑发育成熟。”[61]
深度结构在人类认知演化和发展中的重要性也在认知神经学家的关注之中。发育时间的改变被认为是人类和其他灵长类动物之间智力发展差异的一个方面[62]。在灵长类中,人类的大脑在出生后的很长时间都具备可塑性,但其他灵长类动物的大脑则在出生时就几乎完全定型。因而,人类在大脑发育最具可塑性的阶段能够接触到更加复杂的外部场景,这可能帮助人类的大脑进行调节以适应快速变化的环境,而不是像其他动物的大脑那样更多地受到遗传结构的限制。这样的发育时间差异也在大脑皮层的发育时间和大脑早期自组织中从刺激环境中获取信息的改变得到体现。当然,伴随着这一可塑性的是更长的儿童期,在此期间人需要依靠抚养者和社会群体的支持和训练。因而这一理论也揭示了人类演化中文化和意识共同进化的现象[63]。
公众视野中的深度学习
深度学习常常被看作是通向真正人工智能的重要一步[64],因而许多机构对深度学习的实际应用抱有浓厚的兴趣。2013年12月,Facebook宣布雇用楊立昆为其新建的人工智能实验室的主管,这一实验室将在加州、伦敦和纽约设立分支机构,帮助Facebook研究利用深度学习算法进行类似自动标记照片中用户姓名这样的任务[65]。
2013年3月,杰弗里·辛顿和他的两位研究生亚历克斯·克里泽夫斯基和伊尔亚·苏茨克维谷歌公司雇用,以提升现有的机器学习产品并协助处理谷歌日益增长的数据。谷歌同时并购了辛顿创办的公司DNNresearch[66]。
2016年3月,以深度學習開發的圍棋程式AlphaGo首度在比賽中擊敗人類頂尖选手,形成廣泛的討論。
批评
对深度学习的主要批评是许多方法缺乏理论支撑。大多数深度结构仅仅是梯度下降的某些变式。尽管梯度下降法已经被充分地研究,但理论涉及的其他算法,例如对比分歧算法,并没有获得充分的研究,其收敛性等问题仍不明确。深度学习方法常常被视为黑盒,大多数的结论确认都由经验而非理论来确定。
也有学者认为,深度学习应当被视为通向真正人工智能的一条途径,而不是一种包罗万象的解决方案。尽管深度学习的能力很强,但和真正的人工智能相比,仍然缺乏诸多重要的能力。理论心理学家加里·马库斯指出:
就现实而言,深度学习只是建造智能机器这一更大挑战中的一部分。这些技术缺乏表达因果关系的手段……缺乏进行逻辑推理的方法,而且远没有具备集成抽象知识,例如物品属性、代表和典型用途的信息。最为强大的人工智能系统,例如IBM的人工智能系统沃森,仅仅把深度学习作为一个包含从贝叶斯推理和演绎推理等技术的复杂技术集合中的组成部分[67]。
深度学习库
参见
- 杰弗里·辛顿
- 深度学习框架比较
参考资料
- Deng, L.; Yu, D. (PDF). Foundations and Trends in Signal Processing. 2014, 7: 3–4 [2015-10-23]. (原始内容存档 (PDF)于2016-03-14).
- Bengio, Yoshua. (PDF). Foundations and Trends in Machine Learning. 2009, 2 (1): 1–127. (原始内容 (PDF)存档于2016-03-04).
- Bengio, Y.; Courville, A.; Vincent, P. . IEEE Transactions on Pattern Analysis and Machine Intelligence. 2013, 35 (8): 1798–1828. arXiv:1206.5538
 .
. - Schmidhuber, J. . Neural Networks. 2015, 61: 85–117. arXiv:1404.7828
 . doi:10.1016/j.neunet.2014.09.003.
. doi:10.1016/j.neunet.2014.09.003. - Bengio, Yoshua; LeCun, Yann; Hinton, Geoffrey. . Nature. 2015, 521: 436–444.
- Glauner, P. (学位论文). Imperial College London, Department of Computing. 2015. arXiv:1508.06535
 .
. - Song, H.A.; Lee, S. Y. . . Lectures Notes in Computer Sciences 8226. Springer Berlin Heidelberg. 2013: 466–473. ISBN 978-3-642-42053-5. doi:10.1007/978-3-642-42054-2_58.
- Olshausen, B. A. . Nature. 1996, 381 (6583): 607–609.
- Collobert, R. . VideoLectures.net. April 2011. 事件发生在 7min 45s [2015-10-31]. (原始内容存档于2020-10-19).
- Gomes, L. . IEEE Spectrum. 20 October 2014 [2015-10-31]. (原始内容存档于2019-12-12).
- K. Fukushima., "Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position," Biol. Cybern., 36, 193–202, 1980
- P. Werbos., "Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences," PhD thesis, Harvard University, 1974.
- LeCun et al., "Backpropagation Applied to Handwritten Zip Code Recognition," Neural Computation, 1, pp. 541–551, 1989.
- S. Hochreiter., "Untersuchungen zu dynamischen neuronalen Netzen," Diploma thesis. Institut f. Informatik, Technische Univ. Munich. Advisor: J. Schmidhuber, 1991.
- S. Hochreiter et al., "Gradient flow in recurrent nets: the difficulty of learning long-term dependencies," In S. C. Kremer and J. F. Kolen, editors, A Field Guide to Dynamical Recurrent Neural Networks. IEEE Press, 2001.
- J. Weng, N. Ahuja and T. S. Huang, "Cresceptron: a self-organizing neural network which grows adaptively (页面存档备份,存于)," Proc. International Joint Conference on Neural Networks, Baltimore, Maryland, vol I, pp. 576-581, June, 1992.
- J. Weng, N. Ahuja and T. S. Huang, "Learning recognition and segmentation of 3-D objects from 2-D images (页面存档备份,存于)," Proc. 4th International Conf. Computer Vision, Berlin, Germany, pp. 121-128, May, 1993.
- J. Weng, N. Ahuja and T. S. Huang, "Learning recognition and segmentation using the Cresceptron (页面存档备份,存于)," International Journal of Computer Vision, vol. 25, no. 2, pp. 105-139, Nov. 1997.
- G. E. Hinton., "Learning multiple layers of representation," Trends in Cognitive Sciences, 11, pp. 428–434, 2007.
- J. Schmidhuber., "Learning complex, extended sequences using the principle of history compression," Neural Computation, 4, pp. 234–242, 1992.
- J. Schmidhuber., "My First Deep Learning System of 1991 + Deep Learning Timeline 1962–2013."
- D. C. Ciresan et al., "Deep Big Simple Neural Nets for Handwritten Digit Recognition," Neural Computation, 22, pp. 3207–3220, 2010.
- R. Raina, A. Madhavan, A. Ng., "Large-scale Deep Unsupervised Learning using Graphics Processors," Proc. 26th Int. Conf. on Machine Learning, 2009.
- J. Weng, J. McClelland, A. Pentland, O. Sporns, I. Stockman, M. Sur and E. Thelen, "Autonomous Mental Development by Robots and Animals (页面存档备份,存于)," Science, vol. 291, no. 5504, pp. 599 - 600, Jan. 26, 2001.
- J. Weng, "Brains as Naturally Emerging Turing Machines (页面存档备份,存于)," in Proc. International Joint Conference on Neural Networks, Killarney, Ireland, 8 pages, July 12-17. 2015.
- M Riesenhuber, T Poggio. Hierarchical models of object recognition in cortex. Nature neuroscience, 1999(11) 1019–1025.
- Y. LeCun, B. Boser, J. S. Denker, D. Henderson, R. E. Howard, W. Hubbard, L. D. Jackel. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Computation, 1(4):541–551, 1989.
- S. Hochreiter. Untersuchungen zu dynamischen neuronalen Netzen. Diploma thesis, Institut f. Informatik, Technische Univ. Munich, 1991. Advisor: J. Schmidhuber
- S. Hochreiter, Y. Bengio, P. Frasconi, and J. Schmidhuber. Gradient flow in recurrent nets: the difficulty of learning long-term dependencies. In S. C. Kremer and J. F. Kolen, editors, A Field Guide to Dynamical Recurrent Neural Networks. IEEE Press, 2001.
- Hochreiter, Sepp; and Schmidhuber, Jürgen; Long Short-Term Memory, Neural Computation, 9(8):1735–1780, 1997
- Graves, Alex; and Schmidhuber, Jürgen; Offline Handwriting Recognition with Multidimensional Recurrent Neural Networks, in Bengio, Yoshua; Schuurmans, Dale; Lafferty, John; Williams, Chris K. I.; and Culotta, Aron (eds.), Advances in Neural Information Processing Systems 22 (NIPS'22), December 7th–10th, 2009, Vancouver, BC, Neural Information Processing Systems (NIPS) Foundation, 2009, pp. 545–552
- A. Graves, M. Liwicki, S. Fernandez, R. Bertolami, H. Bunke, J. Schmidhuber. A Novel Connectionist System for Improved Unconstrained Handwriting Recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 31, no. 5, 2009.
- Sven Behnke. (PDF). Lecture Notes in Computer Science 2766. Springer. 2003 [2014-09-16]. (原始内容存档 (PDF)于2021-03-08).
-
Smolensky, P. 1. 1986: 194–281.
|journal=被忽略 (帮助) - Hinton, G. E.; Osindero, S.; Teh, Y. (PDF). Neural Computation. 2006, 18 (7): 1527–1554 [2014-09-16]. PMID 16764513. doi:10.1162/neco.2006.18.7.1527. (原始内容存档 (PDF)于2015-12-23).
- Geoffrey Hinton. . Scholarpedia. 2009-05-31, 4 (5) [2018-04-02]. ISSN 1941-6016. doi:10.4249/scholarpedia.5947. (原始内容存档于2015-12-04) (英语).
- John Markoff. . New York Times. 25 June 2012 [2014-09-16]. (原始内容存档于2018-07-11).
- Ng, Andrew; Dean, Jeff. (PDF). 2012 [2014-09-16]. (原始内容存档 (PDF)于2017-10-12).
- D. C. Ciresan, U. Meier, J. Masci, L. M. Gambardella, J. Schmidhuber. Flexible, High Performance Convolutional Neural Networks for Image Classification. International Joint Conference on Artificial Intelligence (IJCAI-2011, Barcelona), 2011.
- Martines, H., Bengio, Y., & Yannakakis, G. N. (2013). Learning Deep Physiological Models of Affect. I EEE Computational Intelligence, 8(2), 20.
- D. C. Ciresan, U. Meier, J. Masci, J. Schmidhuber. Multi-Column Deep Neural Network for Traffic Sign Classification. Neural Networks, 2012.
- D. C. Ciresan, U. Meier, J. Schmidhuber. Multi-column Deep Neural Networks for Image Classification. IEEE Conf. on Computer Vision and Pattern Recognition CVPR 2012.
- T. Mikolov et al., "Recurrent neural network based language model," Interspeech, 2010.
- Y. LeCun et al., "Gradient-based learning applied to document recognition," Proceedings of the IEEE, 86 (11), pp. 2278–2324.
- T. Sainath et al., "Convolutional neural networks for LVCSR," ICASSP, 2013.
- G. E. Hinton et al., "Deep Neural Networks for Acoustic Modeling in Speech Recognition: The shared views of four research groups," IEEE Signal Processing Magazine, pp. 82–97, November 2012.
- Y. Bengio et al., "Advances in optimizing recurrent networks," ICASSP', 2013.
- G. Dahl et al., "Improving DNNs for LVCSR using rectified linear units and dropout," ICASSP', 2013.
- G. E. Hinton., "A Practical Guide to Training Restricted Boltzmann Machines," Tech. Rep. UTML TR 2010-003, Dept. CS., Univ. of Toronto, 2010.
- G.E. Hinton., "Deep belief networks," Scholarpedia, 4(5):5947.
- H. Larochelle et al., "An empirical evaluation of deep architectures on problems with many factors of variation," in Proc. 24th Int. Conf. Machine Learning, pp. 473–480, 2007.
- . [2014-09-16]. (原始内容存档于2020-10-29).
- Honglak Lee; Roger Grosse; Rajesh Ranganath; Andrew Y. Ng. . ICML '09. 2009: 609–616.
- TIMIT Acoustic-Phonetic Continuous Speech Corpus Linguistic Data Consortium, Philadelphia.
- http://yann.lecun.com/exdb/mnist/ (页面存档备份,存于).
- D. Ciresan, U. Meier, J. Schmidhuber., "Multi-column Deep Neural Networks for Image Classification," Technical Report No. IDSIA-04-12', 2012.
- P. E. Utgoff and D. J. Stracuzzi., "Many-layered learning," Neural Computation, 14, pp. 2497–2529, 2002.
- J. Elman, et al., "Rethinking Innateness," 1996.
- J. Shrager, MH Johnson., "Dynamic plasticity influences the emergence of function in a simple cortical array," Neural Networks, 9 (7), pp. 1119–1129, 1996
- SR Quartz and TJ Sejnowski., "The neural basis of cognitive development: A constructivist manifesto," Behavioral and Brain Sciences, 20 (4), pp. 537–556, 1997.
- S. Blakeslee., "In brain's early growth, timetable may be critical," The New York Times, Science Section, pp. B5–B6, 1995.
- {BUFILL} E. Bufill, J. Agusti, R. Blesa., "Human neoteny revisited: The case of synaptic plasticity," American Journal of Human Biology, 23 (6), pp. 729–739, 2011.
- J. Shrager and M. H. Johnson., "Timing in the development of cortical function: A computational approach," In B. Julesz and I. Kovacs (Eds.), Maturational windows and adult cortical plasticity, 1995.
- D. Hernandez., "The Man Behind the Google Brain: Andrew Ng and the Quest for the New AI (页面存档备份,存于)," Wired, 10 May 2013.
- C. Metz., "Facebook's 'Deep Learning' Guru Reveals the Future of AI (页面存档备份,存于)," Wired, 12 December 2013.
- . CSDN. 2013-03-13 [2014-07-20]. (原始内容存档于2020-03-24).
- G. Marcus., "Is "Deep Learning" a Revolution in Artificial Intelligence?" The New Yorker, 25 November 2012.
- . [2017-07-21]. (原始内容存档于2020-12-08).
- Caffe (页面存档备份,存于)
- . [2018-05-02]. (原始内容存档于2020-11-28).
- . [2017-03-17]. (原始内容存档于2017-08-18).
外部链接
- 来自蒙特利尔大学的深度学习信息 (页面存档备份,存于)
- 杰弗里·辛顿的主页 (页面存档备份,存于)
- 深度学习视频教程 (页面存档备份,存于)
- 燕乐存的主页 (页面存档备份,存于)
- 麻省理工大学生物和计算学习中心 (CBCL) (页面存档备份,存于)
- 斯坦福大学提供的无监督特征学习和深度学习教程 (页面存档备份,存于)
- 谷歌DistBelief框架 (页面存档备份,存于)
- Theano深度学习工具包(使用Python) (页面存档备份,存于)
- Deeplearning4j开源深度学习工具包(使用Java) (页面存档备份,存于)
- NIPS 2013会议(介绍深度学习相关资料) (页面存档备份,存于)