磁化率
定義
磁化率,通常標記為 ,以方程式定義為
- ;
其中, 是物質的磁化强度(單位體積的磁偶極矩), 是磁場強度。
滿足這定義的物質,通常稱為線性介質。採用國際單位制, 定義為
- ;
其中, 是真空磁導率, 是磁感應強度。
所以, 可以表達為
- ;
其中, 是相對磁導率, 是磁導率。
磁化率與相對磁導率的關係方程式為
- 。
磁化率與磁導率的關係方程式為
- 。
磁化率的正負號:抗磁性和其它種磁性
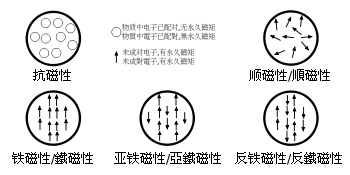
若 為正值,則 ,物質的磁性是順磁性、鐵磁性、亞鐵磁性或反鐵磁性。對於這案例,物質的置入會使得 增強;
若 為負值,則 ,物質的磁性是抗磁性,物質的置入會使得 減弱[1]。
對於順磁性或抗磁性物質,通常 的絕對值都很小,大約在 10-6 到 10-5 之間,大多時候可以忽略為 0 。
在真空裏,磁化率是 0 ,相對磁導率是 1 ,磁導率等於真空磁導率,值為 。
測量磁化率的方法
簡言之,施加具有梯度的磁場於物質樣品,然後測量樣品感受到的作用力差值,代入相關公式,即可得到磁化率[2]。早期,科學家使用古依天平來測量磁化率。測試的樣品懸掛在電磁鐵的兩極之間。由於電磁鐵作用,樣品的表觀重量會與磁化率成正比[3]。讀得古依天平所顯示的表觀重量值後,代入相關公式中。即可得到磁化率。現今,高端測量系統使用超導磁鐵來得到更準確的磁化率。還有一種新穎的產品,稱為艾凡斯天平,廣泛地使用於全世界的課堂及研發實驗室。它測量的是,在置入樣品之前與之後,強大磁鐵所感受到的作用力差值[4]。另外,對於樣品溶液,應用核磁共振科技,可以測量出其磁化率。只要比較樣品溶液與參考溶液的核磁共振頻率的差異,代入公式,即可求得樣品溶液的磁化率[5][6][7]。
張量磁化率
大多數晶體的磁化率不是純量。當施加 於晶體,所響應 () 的磁化強度 與晶體的取向有關,因此可能不與磁場強度 同方向。將磁化率以張量來定義:
- ;
其中,下標 和 指的是向量沿著某個坐標軸的分量(例如,直角坐標系的x-軸、y-軸和 z-軸)。
是個二階張量,因次為 ,描述因為外磁場施加於 j 方向,而產生的磁化強度在 i 方向的分量。
國際單位制與 CGS 單位制之間的單位轉換
前面所述定義和方程式都採用國際單位制 () 。但在很多磁化率的表格中都採用 CGS單位制 (常標記為 emu 或 e.m.u. , 電磁單位的英文簡寫)。它們都依靠著不同定義的真空磁導率[8]:
- 。
CGS 單位制的無因次的磁化率,乘以 ,就可以得到國際單位制的無因次的磁化率[8]:
- 。
例如,在 20°C ,水的磁化率,在國際單位制是 −9.04×10−6,在 CGS 單位制是 −7.19×10−7 。
質量磁化率和莫耳磁化率
質量磁化率 定義為
其中, 是密度,其單位,在國際單位制是 kg·m-3,在CGS 單位制是 g·cm-3。
質量磁化率的單位,在國際單位制是 m3·kg-1,在CGS 單位制是 cm3·g-1。
莫耳磁化率 則定義為
- ;
其中, 是莫耳質量,其單位,在國際單位制是 kg·mole-1,在CGS 單位制是 g·mole-1。
莫耳磁化率的單位,在國際單位制是 m3·mol-1,在CGS 單位制是 cm3·mole-1。
磁化率表格
| 物質 | 溫度 | 氣壓 | (莫耳質量) | (密度) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 單位 | (°C) | (atm) | SI (m3·mol−1) | CGS (cm3·mol−1) | SI (m3·kg−1) | CGS (cm3·g−1) | SI | CGS (emu) | (g/mol) | (g/cm3) |
| 真空 | 任意 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | – | 0 |
| 水 [9] | 20 | 1 | −1.631×10−10 | −1.298×10−5 | −9.051×10−9 | −7.203×10−7 | −9.035×10−6 | −7.190×10−7 | 18.015 | 0.9982 |
| Bi [10] | 20 | 1 | −3.55×10−9 | −2.82×10−4 | −1.70×10−8 | −1.35×10−6 | −1.66×10−4 | −1.32×10−5 | 208.98 | 9.78 |
| 鑽石 [11] | 室溫 | 1 | −6.9×10−11 | −5.5×10−6 | −5.8×10−9 | −4.6×10−7 | −2.0×10−5 | −1.6×10−6 | 12.01 | 3.513 |
| He [12] | 20 | 1 | −2.38×10−11 | −1.89×10−6 | −5.93×10−9 | −4.72×10−7 | −9.85×10−10 | −7.84×10−11 | 4.0026 | 0.000166 |
| Xe [12] | 20 | 1 | −5.71×10−10 | −4.54×10−5 | −4.35×10-9 | −3.46×10−7 | −2.37×10−8 | −1.89×10−9 | 131.29 | 0.00546 |
| O2 [12] | 20 | 0.209 | 4.3×10−8 | 3.42×10−3 | 1.34×10−6 | 1.07×10−4 | 3.73×10−7 | 2.97×10−8 | 31.99 | 0.000278 |
| N2 [12] | 20 | 0.781 | −1.56×10−10 | −1.24×10−5 | −5.56×10−9 | −4.43×10−7 | −5.06×10−9 | −4.03×10−10 | 28.01 | 0.000910 |
| Al | 1 | 2.2×10−10 | 1.7×10−5 | 7.9×10−9 | 6.3×10−7 | 2.2×10−5 | 1.75×10−6 | 26.98 | 2.70 | |
| Ag [13] | 961 | 1 | −2.31×10−5 | −1.84×10−6 | 107.87 | |||||
參考文獻
- . [2009-07-22]. (原始内容存档于2012-06-03).
- L. N. Mulay. A. Weissberger and B. W. Rossiter , 编. 4. Wiley-Interscience: New York. 1972: 431.
- Saunderson, A., , Physics Education, 1968, 3: 272–273, doi:10.1088/0031-9120/3/5/007
- . [2009-07-22]. (原始内容存档于2011-07-16).
- K. Frei and H. J. Bernstein, , J. Chem. Phys., 1962, 37: 1891–1892, doi:10.1063/1.1733393
- Robert Engel, Donald Halpern, and Susan Bienenfeld, , Anal. Chem., 1973, 45: 367–369, doi:10.1021/ac60324a054
- P. W. Kuchel, B. E. Chapman, W. A. Bubb, P. E. Hansen, C. J. Durrant, and M. P. Hertzberg, , Concepts Magn. Reson., 2003, A 18: 56–71, doi:10.1002/cmr.a.10066
- Bennett, L. H.; Page, C. H.; and Swartzendruber, L. J., , Journal of Research of the National Bureau of Standards, 1978, 83 (1): 9–12
- G. P. Arrighini, M. Maestro, and R. Moccia, , J. Chem. Phys., 1968, 49: 882–889, doi:10.1063/1.1670155
- S. Otake, M. Momiuchi and N. Matsuno, , J. Phys. Soc. Jap., 1980, 49 (5): 1824–1828, doi:10.1143/JPSJ.49.1824。必須計算張量對於所有取向的平均值: .
- J. Heremans, C. H. Olk and D. T. Morelli, , Phys. Rev. B, 1994, 49 (21): 15122–15125, doi:10.1103/PhysRevB.49.15122
- R. E. Glick, , J. Phys. Chem., 1961, 65 (9): 1552–1555, doi:10.1021/j100905a020
- R. Dupree and C. J. Ford, , Phys. Rev. B, 1973, 8 (4): 1780–1782, doi:10.1103/PhysRevB.8.1780