梯度

在向量微积分中，梯度（英語：）是一种关于多元导数的概括[1]。平常的一元（单变量）函数的导数是标量值函数，而多元函数的梯度是向量值函数。多元可微函数 $f$ 在点 $P$ 上的梯度，是以 $f$ 在 $P$ 上的偏导数为分量的向量[2]。

上面两个图中，标量场的值用灰度表示，越暗表示越大的数值，而其相应的梯度用藍色箭头表示。

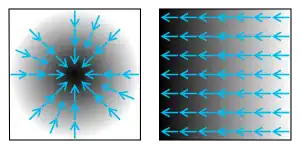
就像一元函数的导数表示这个函数图形的切线的斜率[3]，如果多元函数在点 $P$ 上的梯度不是零向量，則它的方向是这个函数在 $P$ 上最大增长的方向、而它的量是在这个方向上的增长率[4]。

梯度向量中的幅值和方向是与坐标的选择无关的独立量[5]。

在欧几里德空间或更一般的流形之间的多元可微映射的向量值函数的梯度推广是雅可比矩阵[6]。在巴拿赫空间之间的函数的进一步推广是弗雷歇导数。

梯度的解释

将2D函数

f (x, y) = xe -(x 2 + y 2)

的梯度绘制为蓝色箭头，还绘制了这个函数的伪色图。

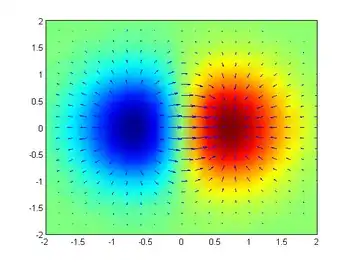
假設有一个房间，房间内所有点的温度由一个标量场 $\phi$ 给出的，即点 $(x,y,z)$ 的温度是 $\phi (x,y,z)$ 。假设温度不随时间改变。然后，在房间的每一点，该点的梯度将显示变热最快的方向。梯度的大小将表示在该方向上的溫度變化率。

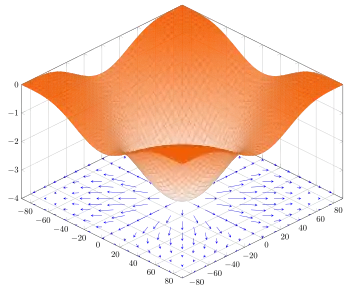
考虑一座高度在 $(x,y)$ 点是 $H(x,y)$ 的山。 $H$ 这一点的梯度是在该点坡度（或者说斜度）最陡的方向。梯度的大小告诉我们坡度到底有多陡。

梯度也可以告诉我们一个数量在不是最快变化方向的其他方向的变化速度。再次考虑山坡的例子。可以有条直接上山的路其坡度是最大的，则其坡度是梯度的大小。也可以有一条和上坡方向成一个角度的路，例如投影在水平面上的夹角为60°。则，若最陡的坡度是40%，这条路的坡度小一点，是20%，也就是40%乘以60°的余弦。

这个现象可以如下数学的表示。山的高度函数 $H$ 的梯度点积一个单位向量给出表面在该向量的方向上的斜率。这称为方向導數。

定義

将函数

f (x, y) = -(cos 2 x + cos 2 y) 2

的梯度描绘为在底面上投影的向量场。

純量函数 $f\colon \mathbb {R} ^{n}\mapsto \mathbb {R}$ 的梯度表示為： $\nabla f$ 或 $\operatorname {grad} f$ ，其中 $\nabla$ （nabla）表示向量微分算子。

函數 $f$ 的梯度， $\nabla f$ ，為向量場且對任意單位向量 $v$ 滿足下列方程式:

{\big (}\nabla f(x){\big )}\cdot \mathbf {v} =D_{\mathbf {v} }f(x)

。

直角坐標系

$\nabla f$ 在三维直角坐标系中表示为

\nabla f={\begin{pmatrix}{\frac {\partial f}{\partial x}},{\frac {\partial f}{\partial y}},{\frac {\partial f}{\partial z}}\end{pmatrix}}={\frac {\partial f}{\partial x}}\mathbf {i} +{\frac {\partial f}{\partial y}}\mathbf {j} +{\frac {\partial f}{\partial z}}\mathbf {k}

，

$i$ , $j$ , $k$ 為標準的單位向量，分別指向 $x$ , $y$ 跟 $z$ 座標的方向。（参看偏导数和向量。）

虽然使用坐标表达，但结果是在正交变换下不变，从几何的观点来看，这是应该的。

舉例來講，函数 $f(x,y,z)=2x+3y^{2}-\sin(z)$ 的梯度为：

\nabla f={\begin{pmatrix}{2},{6y},{-\cos(z)}\end{pmatrix}}=2\mathbf {i} +6y\mathbf {j} -\cos(z)\mathbf {k}

。

圓柱坐標系

在圓柱坐標系中， $f$ 的梯度為：[7]

\nabla f(\rho ,\varphi ,z)={\frac {\partial f}{\partial \rho }}\mathbf {e} _{\rho }+{\frac {1}{\rho }}{\frac {\partial f}{\partial \varphi }}\mathbf {e} _{\varphi }+{\frac {\partial f}{\partial z}}\mathbf {e} _{z}

，

$ρ$ 是 P 點與 z-軸的垂直距離。 $φ$ 是線 OP 在 xy-面的投影線與正 x-軸之間的夾角。 $z$ 與直角坐標的 $z$ 等值。 $e ρ$ , $e φ$ 跟 $e z$ 為單位向量，指向座標的方向。

球坐標系

在球坐標系中：

\nabla f(r,\theta ,\varphi )={\frac {\partial f}{\partial r}}\mathbf {e} _{r}+{\frac {1}{r}}{\frac {\partial f}{\partial \theta }}\mathbf {e} _{\theta }+{\frac {1}{r\sin \theta }}{\frac {\partial f}{\partial \varphi }}\mathbf {e} _{\varphi }

，

其中 $θ$ 为极角， $φ$ 方位角。

实值函数相对于向量和矩阵的梯度

相对于n×1向量x的梯度算子记作 $\nabla _{\boldsymbol {x}}$ ，定义为[8]

\nabla _{\boldsymbol {x}}{\overset {\underset {\mathrm {def} }{}}{=}}\left[{\frac {\partial }{\partial x_{1}}},{\frac {\partial }{\partial x_{2}}},\cdots ,{\frac {\partial }{\partial x_{n}}}\right]^{T}={\frac {\partial }{\partial {\boldsymbol {x}}}}

对向量的梯度

以n×1实向量x为变元的实标量函数f(x)相对于x的梯度为一n×1列向量x，定义为

\nabla _{\boldsymbol {x}}f({\boldsymbol {x}}){\overset {\underset {\mathrm {def} }{}}{=}}\left[{\frac {\partial f({\boldsymbol {x}})}{\partial x_{1}}},{\frac {\partial f({\boldsymbol {x}})}{\partial x_{2}}},\cdots ,{\frac {\partial f({\boldsymbol {x}})}{\partial x_{n}}}\right]^{T}={\frac {\partial f({\boldsymbol {x}})}{\partial {\boldsymbol {x}}}}

m维行向量函数 ${\boldsymbol {f}}({\boldsymbol {x}})=[f_{1}({\boldsymbol {x}}),f_{2}({\boldsymbol {x}}),\cdots ,f_{m}({\boldsymbol {x}})]$ 相对于n维实向量x的梯度为一n×m矩阵，定义为

\nabla _{\boldsymbol {x}}{\boldsymbol {f}}({\boldsymbol {x}}){\overset {\underset {\mathrm {def} }{}}{=}}{\begin{bmatrix}{\frac {\partial f_{1}({\boldsymbol {x}})}{\partial x_{1}}}&{\frac {\partial f_{2}({\boldsymbol {x}})}{\partial x_{1}}}&\cdots &{\frac {\partial f_{m}({\boldsymbol {x}})}{\partial x_{1}}}\\{\frac {\partial f_{1}({\boldsymbol {x}})}{\partial x_{2}}}&{\frac {\partial f_{2}({\boldsymbol {x}})}{\partial x_{2}}}&\cdots &{\frac {\partial f_{m}({\boldsymbol {x}})}{\partial x_{2}}}\\\vdots &\vdots &\ddots &\vdots \\{\frac {\partial f_{1}({\boldsymbol {x}})}{\partial x_{n}}}&{\frac {\partial f_{2}({\boldsymbol {x}})}{\partial x_{n}}}&\cdots &{\frac {\partial f_{m}({\boldsymbol {x}})}{\partial x_{n}}}\\\end{bmatrix}}={\frac {\partial {\boldsymbol {f}}({\boldsymbol {x}})}{\partial {\boldsymbol {x}}}}

对矩阵的梯度

标量函数 $f({\boldsymbol {A}})$ 相对于m×n实矩阵A的梯度为一m×n矩阵，简称梯度矩阵，定义为

\nabla _{\boldsymbol {A}}f({\boldsymbol {A}}){\overset {\underset {\mathrm {def} }{}}{=}}{\begin{bmatrix}{\frac {\partial f({\boldsymbol {A}})}{\partial a_{11}}}&{\frac {\partial f({\boldsymbol {A}})}{\partial a_{12}}}&\cdots &{\frac {\partial f({\boldsymbol {A}})}{\partial a_{1n}}}\\{\frac {\partial f({\boldsymbol {A}})}{\partial a_{21}}}&{\frac {\partial f({\boldsymbol {A}})}{\partial a_{22}}}&\cdots &{\frac {\partial f({\boldsymbol {A}})}{\partial a_{2n}}}\\\vdots &\vdots &\ddots &\vdots \\{\frac {\partial f({\boldsymbol {A}})}{\partial a_{m1}}}&{\frac {\partial f({\boldsymbol {A}})}{\partial a_{m2}}}&\cdots &{\frac {\partial f({\boldsymbol {A}})}{\partial a_{mn}}}\\\end{bmatrix}}={\frac {\partial f({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}

法则

以下法则适用于实标量函数对向量的梯度以及对矩阵的梯度。

线性法则：若 $f({\boldsymbol {A}})$ 和 $g({\boldsymbol {A}})$ 分别是矩阵A的实标量函数，c₁和c₂为实常数，则
${\frac {\partial [c_{1}f({\boldsymbol {A}})+c_{2}g({\boldsymbol {A}})]}{\partial {\boldsymbol {A}}}}=c_{1}{\frac {\partial f({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}+c_{2}{\frac {\partial g({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}$

乘积法则：若 $f({\boldsymbol {A}})$ ， $g({\boldsymbol {A}})$ 和 $h({\boldsymbol {A}})$ 分别是矩阵A的实标量函数，则
${\frac {\partial f({\boldsymbol {A}})g({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}=g({\boldsymbol {A}}){\frac {\partial f({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}+f({\boldsymbol {A}}){\frac {\partial g({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}$

${\frac {\partial f({\boldsymbol {A}})g({\boldsymbol {A}})h({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}=g({\boldsymbol {A}})h({\boldsymbol {A}}){\frac {\partial f({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}+f({\boldsymbol {A}})h({\boldsymbol {A}}){\frac {\partial g({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}+f({\boldsymbol {A}})g({\boldsymbol {A}}){\frac {\partial h({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}$

商法则：若 $g({\boldsymbol {A}})\neq 0$ ，则
${\frac {\partial f({\boldsymbol {A}})/g({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}={\frac {1}{g({\boldsymbol {A}})^{2}}}\left[g({\boldsymbol {A}}){\frac {\partial f({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}-f({\boldsymbol {A}}){\frac {\partial g({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}\right]$

链式法则：若A为m×n矩阵，且 $y=f({\boldsymbol {A}})$ 和 $g(y)$ 分别是以矩阵A和标量y为变元的实标量函数，则
${\frac {\partial g(f({\boldsymbol {A}}))}{\partial {\boldsymbol {A}}}}={\frac {dg(y)}{dy}}{\frac {\partial f({\boldsymbol {A}})}{\partial {\boldsymbol {A}}}}$

流形上的梯度

一个黎曼流形 $M$ 上的对于任意可微函数 $f$ 的梯度 $\nabla f$ 是一个向量场，使得对于每个向量 $\xi$ ，

{\displaystyle \langle \nabla f,\xi \rangle

其中 $\langle \cdot ,\cdot \rangle$ 代表 $M$ 上的内积（度量）而 $\xi f(p),p\in M$ 是 $f$ 在點 $p$ ，方向為 $\xi (p)$ 的方向導數。换句话说，如果 $\varphi :U\subseteq M\mapsto \mathbb {R} ^{n}$ 為 $p$ 附近的局部座標，在此座標下有 $\xi (x)=\sum _{j}a_{j}(x){\frac {\partial }{\partial x_{j}}}$ ,則 $\xi f(p)$ 将成为：

\xi (f\mid _{p}):=\sum _{j}a_{j}({\frac {\partial }{\partial x_{j}}}(f\circ \varphi ^{-1})\mid _{\varphi (p)})

。

函数的梯度和外微分相关，因为 $\xi f=df(\xi )$ ，实际上內積容许我们可以用一种标准的方式将1-形式 $df$ 和向量场 $\nabla f$ 建立联系。由 $\nabla f$ 的定義， $df(\xi )=\langle \nabla f,\xi \rangle$ ，这样 $f$ 的梯度可以"等同"于0-形式的外微分 $df$ ，這裡"等同"意味著：兩集合 $\{df\}$ 和 $\{\nabla f\}$ 之間有1對1的滿射。

由定義可算流形上 $\nabla f$ 的局部座標表達式為：

\nabla f=\sum _{ik}g^{ik}{\frac {\partial f}{\partial x^{k}}}{\frac {\partial }{\partial x^{i}}}

。

請注意這是流形上對黎曼度量 $ds^{2}=\sum _{ij}g_{ij}dx^{i}dx^{j}$ 的公式，跟 $\mathbb {R} ^{n}$ 裡直角座標的公式不同。常常我們寫時會省略求和 $\sum$ 符號，不過為了避免混淆，在這裡的公式還是加上去了。

参看

雅可比矩阵
散度
旋度
偏导数
索貝爾算子
向量分析
离子梯度
梯度下降法
等位集合（Level set）
外微分
在圆柱和球坐标系中的del

参考文献

引用

Beauregard & Fraleigh (1973, p. 84)
Bachman (2007, p. 76)
Beauregard & Fraleigh (1973, p. 84)
Downing (2010, p. 316)
Harper (1976, p. 15)
Kreyszig (1972, p. 307)
McGraw-Hill (2007, p. 196)
Moise (1967, p. 683)
Protter & Morrey, Jr. (1970, p. 714)
Swokowski et al. (1994, p. 1038)
Protter & Morrey, Jr. (1970, pp. 21,88)
Bachman (2007, p. 77)
Downing (2010, pp. 316–317)
Kreyszig (1972, p. 309)
McGraw-Hill (2007, p. 196)
Moise (1967, p. 684)
Protter & Morrey, Jr. (1970, p. 715)
Swokowski et al. (1994, pp. 1036,1038–1039)
Kreyszig (1972, pp. 308–309)
Stoker (1969, p. 292)
Beauregard & Fraleigh (1973, pp. 87,248)
Kreyszig (1972, pp. 333,353,496)
Schey 1992，第139–142頁.
张贤达 (2004, p. 258)

来源

书籍

Bachman, David, , New York: McGraw-Hill, 2007, ISBN 0-07-148121-4
Beauregard, Raymond A.; Fraleigh, John B., , Boston: Houghton Mifflin Company, 1973, ISBN 0-395-14017-X
Downing, Douglas, Ph.D., , New York: Barron's, 2010, ISBN 978-0-7641-4461-5
Dubrovin, B. A.; Fomenko, A. T.; Novikov, S. P. . Graduate Texts in Mathematics 2nd. Springer. 1991. ISBN 978-0-387-97663-1.
Harper, Charlie, , New Jersey: Prentice-Hall, 1976, ISBN 0-13-487538-9
Kreyszig, Erwin, 3rd, New York: Wiley, 1972, ISBN 0-471-50728-8
10th. New York: McGraw-Hill. 2007. ISBN 0-07-144143-3.
Moise, Edwin E., , Reading: Addison-Wesley, 1967
Protter, Murray H.; Morrey, Jr., Charles B., 2nd, Reading: Addison-Wesley, 1970, LCCN 76087042
Schey, H. M. 2nd. W. W. Norton. 1992. ISBN 0-393-96251-2. OCLC 25048561.
Stoker, J. J., , New York: Wiley, 1969, ISBN 0-471-82825-4
Swokowski, Earl W.; Olinick, Michael; Pence, Dennis; Cole, Jeffery A., 6th, Boston: PWS Publishing Company, 1994, ISBN 0-534-93624-5
张贤达, , 清华大学出版社, 2004, ISBN 9787302092711 （中文（中国大陆））

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Beauregard & Fraleigh (1973, p. 84)

[2] Bachman (2007, p. 76)
Beauregard & Fraleigh (1973, p. 84)
Downing (2010, p. 316)
Harper (1976, p. 15)
Kreyszig (1972, p. 307)
McGraw-Hill (2007, p. 196)
Moise (1967, p. 683)
Protter & Morrey, Jr. (1970, p. 714)
Swokowski et al. (1994, p. 1038)

[3] Protter & Morrey, Jr. (1970, pp. 21,88)

[4] Bachman (2007, p. 77)
Downing (2010, pp. 316–317)
Kreyszig (1972, p. 309)
McGraw-Hill (2007, p. 196)
Moise (1967, p. 684)
Protter & Morrey, Jr. (1970, p. 715)
Swokowski et al. (1994, pp. 1036,1038–1039)

[5] Kreyszig (1972, pp. 308–309)
Stoker (1969, p. 292)

[6] Beauregard & Fraleigh (1973, pp. 87,248)
Kreyszig (1972, pp. 333,353,496)

[Schey-1992-7] Schey 1992，第139–142頁.

[8] 张贤达 (2004, p. 258)