邏輯斯諦迴歸
邏輯斯諦迴歸(英語:,又譯作邏輯斯迴歸、羅吉斯迴歸、、对数几率迴归),在统计学中是一種对数几率模型(英語:,又译作逻辑斯谛模型、评定模型、分类评定模型),是离散选择法模型之一,属于多元变量分析范畴,是社会学、生物统计学、临床、数量心理学、计量经济学、市场营销等统计实证分析的常用方法。
通过使事件的对数发生率(log-odd)成为一个或多个自变量的线性组合,对事件发生的概率进行建模。形式上,在二元逻辑回归中,有一个二元因变量,由指示变量编码,其中两个值标记为“0”和“1”,而自变量每个都可以是二元变量(两个类,由指示变量)或连续变量(任何实值)。标记为“1”的值的相应概率可以在0和1之间变化;将对数发生率转换为概率的函数就是逻辑斯諦函数,因此得名。对数发生率单位称为logit,来自logistic unit。[1]
二元变量在统计学中广泛用于对某一类别或事件发生概率的建模,例如团队获胜概率、患者健康概率等,而其中,逻辑模型则自大约 1970年以来最常用的二元回归模型。[2]当存在两个以上可能值(例如图像是否是猫、狗、狮子等)时,二元变量可以推广为分类变量,并且二元逻辑回归推广为多项逻辑回归。如果多个类别是有序的,则可以使用序数逻辑回归。逻辑回归模型本身只是简单地根据输入对输出概率进行建模,并不执行统计分类。[3]
例子
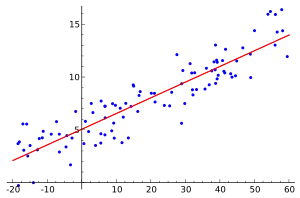
以一个例子说明逻辑回归如何解决实际问题:
一个小组20名学生,各自花费0~6小时准备考试,他们不同的学习时数如何影响通过考试的概率?
问题中的因变量是考试“通过”或者“挂科”,这是用逻辑回归的原因,虽然分别用“1”和“0”表示,但这两个数字不代表基数。如果问题发生变化,用0-100的成绩(基数)代替通过、挂科,则可以使用回归分析。
下表显示每个学生花费在学习上的小时数,以及他们通过(1)或挂科(0)。
| 小时(xk) | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 | 1.75 | 1.75 | 2.00 | 2.25 | 2.50 | 2.75 | 3.00 | 3.25 | 3.50 | 4.00 | 4.25 | 4.50 | 4.75 | 5.00 | 5.50 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 通过(yk) | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
对学习时间(xk)和测试结果(yk = 1 表示通过,0 表示挂科)组成的数据进行拟合。数据点由下标k索引,该下标从1到20。x变量称为“自变量”,y变量称为“分类变量”,由“通过”或“失败”两个类别组成,分别对应于分类值1和0。
模型

| 统计学系列条目 |
| 迴歸分析 |
|---|
 |
| 模型 |
|
|
|
|
| 估计 |
|
| 背景 |
|
|
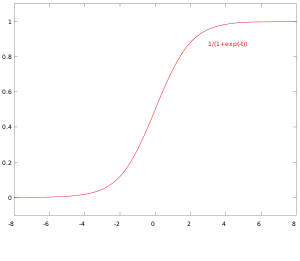
逻辑函数形式为:
其中μ是位置参数(曲线的中点,其中),s是尺度参数。该式可重写为:
称为截距,是直线的y截距。是反比例参数或速率参数,是作为"x"函数的对数发生率的"y"截距和斜率。反之,,并且。
逻辑斯谛分布公式
其中参数常用最大似然估計。
IIA假设
全名為Independent and irrelevant alternatives假设,也称作IIA效应,指Logit模型中的各个可选项是独立的。
IIA假设示例
市场上有A,B,C三个商品相互竞争,分别占有市场份额:60%,30%和10%,三者比例为:6:3:1
一个新产品D引入市场,有能力占有20%的市场——
如果满足IIA假设,各个产品独立作用,互不关联:新产品D占有20%的市场份额,剩下的80%在A、B、C之间按照6:3:1的比例瓜分,分别占有48%,24%和8%。
如果不满足IIA假设,比如新产品D跟产品B相似度高,则新产品D的CP值高而夺去产品B的部分市场(总份额的20%),則产品B剩余10%,而产品A和C的市场份额保持60%和10%不变。
满足IIA假设的优点
- 可以获得每个个性化的选择集合的一致的参数估计
- 各个类别的子集的一般化的估计
- 大大节省时间
- 可选项数目很多的时候尤其如此
Hausman检验
傑里·A·奧斯曼和丹尼爾·麥克法登提出的。
一般化极值模型
可以将可选项间的相关性建模
巢式Logit模型
巢式(Nested)表示可选项被分作不同的组,组与组之间不相关,组内的可选项相关,相关程度用1-λg来表示(1-λg越大,相关程度越高)
应用
配體結合分析
配體結合分析的典型校准曲线是S形的,下边界(渐近线)靠近背景信号(非特异性结合),而上渐近线靠近最大的饱和响应。 四参数逻辑模型通常是拟合这种形状校准曲线的首选,可以准确描述测量信号值与分析物浓度之间的S形关系。当不对称性明显时会添加第五个参数,但可能会导致拟合算法变得不稳定。[4]
二类评定模型(Binary Logit Model)
- 仅有两个可选项:V1n,V2n
| 变量类型 | 统计量 | 组别比较 | 回归模型 |
|---|---|---|---|
| numerical | mean | t-test/ANOVA | 线性回归 |
| categorical | percentage | Chi-square test | 逻辑斯谛回归 |
| persontime | KM estimates (survival curves) |
Log-rank test | 比例风险回归 |
参考书目
- Agresti, Alan: Categorical Data Analysis. New York: Wiley, 1990.
- Amemiya, T., 1985, Advanced Econometrics,Harvard University Press.
- Hosmer, D. W. and S. Lemeshow: Applied logistic regression. New York; Chichester, Wiley, 2000.
参见
- 多重变量分析
外部链接
参考
- Hosmer, David W.; Lemeshow, Stanley. . Wiley series in probability and statistics 2. ed., [Nachdr.] New York: Wiley. 200. ISBN 978-0-471-35632-5. 缺少或
|title=为空 (帮助) - Cramer, J.S. . SSRN Electronic Journal. 2003. ISSN 1556-5068. doi:10.2139/ssrn.360300 (英语).
- Walker, Strother H.; Duncan, David B. . Biometrika. 1967-06, 54 (1/2) [2023-11-11]. doi:10.2307/2333860. (原始内容存档于2024-02-29).
- Findlay, John W. A.; Dillard, Robert F. . The AAPS Journal. 2007-06, 9 (2). ISSN 1550-7416. doi:10.1208/aapsj0902029.
