Z轉換

在數學和信号处理中，Z轉換（英語：）把離散的實數或複數时间訊號從時域轉為复頻域（z域或z平面）表示。

可以把它认为是拉普拉斯变换的离散时间等价。在时标微积分中会探索它们的相似性。

历史

现在所知的Z变换的基本思想，拉普拉斯就已了解，而1947年W. Hurewicz用作求解常系数差分方程的一种容易处理的方式。[1] 后来由1952年哥伦比亚大学的采样控制组的約翰·拉加齊尼和查德称其为“Z变换”。[2][3]

約翰·拉加齊尼后来发展并推广了改进或高级Z变换。[4][5]

Z变换中包含的思想在数学里称作母函数方法，该方法可以追溯到1730年的时候，棣莫弗与概率论结合将其引入。[6] 从数学的角度，当把数字序列视为解析函数的（洛朗）展开时，Z变换也可以看成是洛朗级数。

定義

像很多积分变换一样，Z变换可以有单边和双边定义。

双边Z变换

双边Z轉換把离散時域信号 $x[n]$ 轉為形式幂级数 $X(z)$ 。

X(z)={\mathcal {Z}}\{x[n]\}=\sum _{n=-\infty }^{\infty }x[n]z^{-n}

當中 $n$ 是整數， $z$ 是複數变量，其表示方式為

z=Ae^{j\phi }=A(\cos {\phi }+j\sin {\phi })\,

其中 A 为 z 的模，j 为虚数单位，而 ɸ 为辐角（也叫相位角），用弧度表示。

单边Z变换

另外，只对 n ≥ 0 定义的 x[n]，单边Z变换定义为

X(z)={\mathcal {Z}}\{x[n]\}=\sum _{n=0}^{\infty }x[n]z^{-n}.

在信号处理中，这个定义可以用来计算离散时间因果系统的单位冲激响应。

单边Z变换的一个重要例子是概率母函数，其中 x[n] 部分是离散随机变量取 n 值时的概率，而函数 X(z) 通常写作 X(s)，用 s = z⁻¹ 表示。Z变换的性质（在下面）在概率论背景下有很多有用的解释。

地球物理学定义

地球物理中的Z变换，通常的定义是 z 的幂级数而非 z⁻¹ 的。例如，Enders Anthony Robinson[7]和Ernest R. Kanasewich都使用这个惯例。[8]地球物理定义为：

X(z)={\mathcal {Z}}\{x[n]\}=\sum _{n}x[n]z^{n}.

这两个定义是等价的；但差分结果会有一些不同。例如，零点和极点的位置移动在单位圆内使用一个定义，在单位圆外用另一个定义。[7][8] 因此，需要注意特定作者使用的定义。

逆Z变换

逆Z变换为

x[n]={\mathcal {Z}}^{-1}\{X(z)\}={\frac {1}{2\pi j}}\oint _{C}X(z)z^{n-1}dz

其中 C 是完全处于收敛域（ROC）内的包围原点的一个逆时针闭合路径。在 ROC 是因果的情况下（参见例2），这意味着路径 C 必须包围 X(z) 的所有极点。

这个曲线积分的一个特殊情形出现在 C 是单位圆的时候（可以在ROC包含单位圆的时候使用，总能保证 X(z) 是稳定的，即所有极点都在单位圆内）。逆Z变换可以化简为逆离散傅里叶变换：

x[n]={\frac {1}{2\pi }}\int _{-\pi }^{+\pi }X(e^{j\omega })e^{j\omega n}d\omega .

有限范围 n 和有限数量的均匀间隔的 z 值的Z变换可以用Bluestein的FFT算法方便地计算。离散时间傅里叶变换 (DTFT)—不要与离散傅里叶变换（DFT）混淆—是通过将 z 限制在位于单位圆上而得到的一种Z变换的特殊情况。

收敛域

收敛域（ROC）是指Z变换的求和收敛的复平面上的点集。

ROC=\left\{z:\left|\sum _{n=-\infty }^{\infty }x[n]z^{-n}\right|<\infty \right\}

例1（收敛域不存在）

令 $x[n]=(0.5)^{n}$ 。在区间 $(-\infty ,\infty )$ 上展开 $x[n]$ 成为

x[n]=\left\{\cdots ,0.5^{-3},0.5^{-2},0.5^{-1},1,0.5,0.5^{2},0.5^{3},\cdots \right\}=\left\{\cdots ,2^{3},2^{2},2,1,0.5,0.5^{2},0.5^{3},\cdots \right\}.

观察上面的和

\sum _{n=-\infty }^{\infty }x[n]z^{-n}\to \infty .

因此，没有一个 $z$ 值可以满足这个条件。

例2（因果的收敛域）

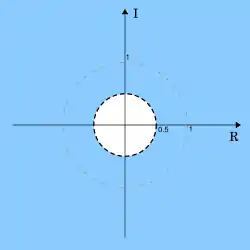
ROC用蓝色表示，单位圆用灰色虚点圆表示（外圈者，而 |z| = 0.5 这个圆用虚线圆表示（內圈者）

令 $x[n]=0.5^{n}u[n]\$ （其中 u 是单位阶跃函数）。在区间 (−∞, ∞) 上展开 x[n] 得到

x[n]=\left\{\cdots ,0,0,0,1,0.5,0.5^{2},0.5^{3},\cdots \right\}.

观察这个和

\sum _{n=-\infty }^{\infty }x[n]z^{-n}=\sum _{n=0}^{\infty }0.5^{n}z^{-n}=\sum _{n=0}^{\infty }\left({\frac {0.5}{z}}\right)^{n}={\frac {1}{1-0.5z^{-1}}}.

最后一个等式来自无穷几何级数，而等式仅在 |0.5z⁻¹| < 1 时成立，可以以 z 为变量写成 |z| > 0.5。因此，收敛域为 |z| > 0.5。在这种情况下，收敛域为复平面“挖掉”原点为中心的半径为 0.5 的圆盘。

例3（非因果的收敛域）

ROC用蓝色表示，单位圆用灰色虚点圆表示（用眼睛看会呈红色），而 |z| = 0.5 这个圆用虚线圆表示

令 $x[n]=-(0.5)^{n}u[-n-1]\$ （其中 u 是单位阶跃函数）。在区间 (−∞, ∞) 上展开 x[n] 得到

x[n]=\left\{\cdots ,-(0.5)^{-3},-(0.5)^{-2},-(0.5)^{-1},0,0,0,0,\cdots \right\}.

观察这个和

\sum _{n=-\infty }^{\infty }x[n]z^{-n}=-\sum _{n=-\infty }^{-1}0.5^{n}z^{-n}=-\sum _{m=1}^{\infty }\left({\frac {z}{0.5}}\right)^{m}=1-{\frac {1}{1-0.5^{-1}z}}={\frac {1}{1-0.5z^{-1}}}

再次使用无穷几何级数，此等式只在 |0.5⁻¹z| < 1 时成立，可以用 z 为变量写成 |z| < 0.5。因此，收敛域为 |z| < 0.5。在这种情况下，收敛域为中心在原点的半径为 0.5 的圆盘。

本例与上例的不同之处仅在收敛域上。这是意图展示只有变换结果是不够的。

实例结论

实例2和3清楚地表明，当且仅当指定收敛域时， $x[n]$ 的Z变换 X(z) 才是唯一的。画因果和非因果情形的零极点图表明，在这两种情况下收敛域都不包含极点位于 0.5 的情形。这可以拓展到多个极点的情形：收敛域永远不会包含极点。

在例2中，因果系统产生一个包含 |z| = ∞ 的收敛域，而例3中的非因果系统产生包含 $|z|=0$ 的收敛域。

ROC表示为蓝色圆环 0.5 < |z| < 0.75

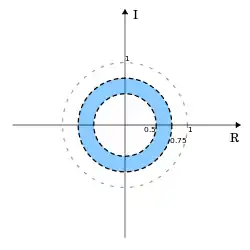
在有多个极点的系统中，收敛域可以既不包含 |z| = ∞ 也不包含 |z| = 0。画出的收敛域与一个圆形带。例如，

x[n]=0.5^{n}u[n]-0.75^{n}u[-n-1]

的极点为 0.5 与 0.75。收敛域会是 0.5 < |z| < 0.75，不包含原点和无穷大。这样的系统称为混合因果系统，因为它包含一个因果项 (0.5)ⁿu[n] 和一个非因果项 −(0.75)ⁿu[−n−1]。

一个系统的稳定性可以只通过了解收敛域来确定。如果收敛域包含单位圆（即 |z| = 1），那么系统是稳定的。在上述系统中因果系统（例2）是稳定的，因为 |z| > 0.5 包含单位圆。

如果我们有一个没有给定收敛域Z变换（即模糊的 $x[n]$ ），则可以确定一个唯一的 $x[n]$ 满足下列：

稳定性
因果性

如果要求满足稳定性，则收敛域必须包含单位圆；如果要求为一个因果系统，则收敛域必须包含无穷大，并且系统函数应为一个右边序列。如果要求为一个非因果系统，那么收敛域必须包含原点，且系统函数为左边序列。如果既要满足稳定性，也要满足因果性，则系统函数的所有极点都必须在单位圆内。

通过这种方法可以找到唯一的 $x[n]$ 。

性质

**Z变换性质**
	时域	Z域	证明	收敛域
记法	$x[n]={\mathcal {Z}}^{-1}\{X(z)\}$	$X(z)={\mathcal {Z}}\{x[n]\}$		$r_{2}<\|z\|<r_{1}$
線性	$a_{1}x_{1}[n]+a_{2}x_{2}[n]$	$a_{1}X_{1}(z)+a_{2}X_{2}(z)$	${\begin{aligned}X(z)&=\sum _{n=-\infty }^{\infty }(a_{1}x_{1}(n)+a_{2}x_{2}(n))z^{-n}\\&=a_{1}\sum _{n=-\infty }^{\infty }x_{1}(n)z^{-n}+a_{2}\sum _{n=-\infty }^{\infty }x_{2}(n)z^{-n}\\&=a_{1}X_{1}(z)+a_{2}X_{2}(z)\end{aligned}}$	包含 ROC₁ ∩ ROC₂
时间膨胀	$x_{K}[n]={\begin{cases}x[r],&n=rK\\0,&n\not =rK\end{cases}}$ r: 整数	$X(z^{K})$	${\begin{aligned}X_{K}(z)&=\sum _{n=-\infty }^{\infty }x_{K}(n)z^{-n}\\&=\sum _{r=-\infty }^{\infty }x(r)z^{-rK}\\&=\sum _{r=-\infty }^{\infty }x(r)(z^{K})^{-r}\\&=X(z^{K})\end{aligned}}$	$R^{\frac {1}{K}}$
降采样	$x[nK]$	${\frac {1}{K}}\sum _{p=0}^{K-1}X\left(z^{\tfrac {1}{K}}\cdot e^{-i{\tfrac {2\pi }{K}}p}\right)$	ohio-state.edu （页面存档备份，存于）或 ee.ic.ac.uk （页面存档备份，存于）
时移	$x[n-k]$	$z^{-k}X(z)$	${\begin{aligned}Z\{x[n-k]\}&=\sum _{n=0}^{\infty }x[n-k]z^{-n}\\&=\sum _{j=-k}^{\infty }x[j]z^{-(j+k)}&&j=n-k\\&=\sum _{j=-k}^{\infty }x[j]z^{-j}z^{-k}\\&=z^{-k}\sum _{j=-k}^{\infty }x[j]z^{-j}\\&=z^{-k}\sum _{j=0}^{\infty }x[j]z^{-j}&&x[\beta ]=0,\beta <0\\&=z^{-k}X(z)\end{aligned}}$	ROC，除了 k > 0 时 z = 0 和 k < 0 时 z = ∞
Z域的尺度性质	$a^{n}x[n]$	$X(a^{-1}z)$	${\begin{aligned}{\mathcal {Z}}\left\{a^{n}x[n]\right\}&=\sum _{n=-\infty }^{\infty }a^{n}x(n)z^{-n}\\&=\sum _{n=-\infty }^{\infty }x(n)(a^{-1}z)^{-n}\\&=X(a^{-1}z)\end{aligned}}$	$\|a\|r_{2}<\|z\|<\|a\|r_{1}$
时间反转	$x[-n]$	$X(z^{-1})$	${\begin{aligned}{\mathcal {Z}}\{x(-n)\}&=\sum _{n=-\infty }^{\infty }x(-n)z^{-n}\\&=\sum _{m=-\infty }^{\infty }x(m)z^{m}\\&=\sum _{m=-\infty }^{\infty }x(m){(z^{-1})}^{-m}\\&=X(z^{-1})\\\end{aligned}}$	${\tfrac {1}{r_{1}}}<\|z\|<{\tfrac {1}{r_{2}}}$
共轭复数	$x^{*}[n]$	$X^{}(z^{})$	${\begin{aligned}{\mathcal {Z}}\{x^{}(n)\}&=\sum _{n=-\infty }^{\infty }x^{}(n)z^{-n}\\&=\sum _{n=-\infty }^{\infty }\left[x(n)(z^{})^{-n}\right]^{}\\&=\left[\sum _{n=-\infty }^{\infty }x(n)(z^{})^{-n}\right]^{}\\&=X^{}(z^{})\end{aligned}}$
实部	$\operatorname {Re} \{x[n]\}$	${\tfrac {1}{2}}\left[X(z)+X^{}(z^{})\right]$
虚部	$\operatorname {Im} \{x[n]\}$	${\tfrac {1}{2j}}\left[X(z)-X^{}(z^{})\right]$
微分	$nx[n]$	$-z{\frac {dX(z)}{dz}}$	${\begin{aligned}{\mathcal {Z}}\{nx(n)\}&=\sum _{n=-\infty }^{\infty }nx(n)z^{-n}\\&=z\sum _{n=-\infty }^{\infty }nx(n)z^{-n-1}\\&=-z\sum _{n=-\infty }^{\infty }x(n)(-nz^{-n-1})\\&=-z\sum _{n=-\infty }^{\infty }x(n){\frac {d}{dz}}(z^{-n})\\&=-z{\frac {dX(z)}{dz}}\end{aligned}}$
卷积	$x_{1}[n]*x_{2}[n]$	$X_{1}(z)X_{2}(z)$	${\begin{aligned}{\mathcal {Z}}\{x_{1}(n)*x_{2}(n)\}&={\mathcal {Z}}\left\{\sum _{l=-\infty }^{\infty }x_{1}(l)x_{2}(n-l)\right\}\\&=\sum _{n=-\infty }^{\infty }\left[\sum _{l=-\infty }^{\infty }x_{1}(l)x_{2}(n-l)\right]z^{-n}\\&=\sum _{l=-\infty }^{\infty }x_{1}(l)\left[\sum _{n=-\infty }^{\infty }x_{2}(n-l)z^{-n}\right]\\&=\left[\sum _{l=-\infty }^{\infty }x_{1}(l)z^{-l}\right]\!\!\left[\sum _{n=-\infty }^{\infty }x_{2}(n)z^{-n}\right]\\&=X_{1}(z)X_{2}(z)\end{aligned}}$	包含 ROC₁ ∩ ROC₂
互相关	$r_{x_{1},x_{2}}=x_{1}^{}[-n]x_{2}[n]$	$R_{x_{1},x_{2}}(z)=X_{1}^{}({\tfrac {1}{z^{}}})X_{2}(z)$		包含 $X_{1}({\tfrac {1}{z^{*}}})$ 与 $X_{2}(z)$ 的ROC的交集
一阶差分	$x[n]-x[n-1]$	$(1-z^{-1})X(z)$		包含 X₁(z) 与 z ≠ 0 的ROC的交集
累积	$\sum _{k=-\infty }^{n}x[k]$	${\frac {1}{1-z^{-1}}}X(z)$	${\begin{aligned}\sum _{n=-\infty }^{\infty }\sum _{k=-\infty }^{n}x[k]z^{-n}&=\sum _{n=-\infty }^{\infty }(x[n]+\cdots +x[-\infty ])z^{-n}\\&=X[z]\left(1+z^{-1}+z^{-2}+\cdots \right)\\&=X[z]\sum _{j=0}^{\infty }z^{-j}\\&=X[z]{\frac {1}{1-z^{-1}}}\end{aligned}}$
乘法	$x_{1}[n]x_{2}[n]$	${\frac {1}{j2\pi }}\oint _{C}X_{1}(v)X_{2}({\tfrac {z}{v}})v^{-1}\mathrm {d} v$		-

帕塞瓦尔定理

\sum _{n=-\infty }^{\infty }x_{1}[n]x_{2}^{*}[n]\quad =\quad {\frac {1}{j2\pi }}\oint _{C}X_{1}(v)X_{2}^{*}({\tfrac {1}{v^{*}}})v^{-1}\mathrm {d} v

初值定理：如果 x[n] 为因果的，那么

x[0]=\lim _{z\to \infty }X(z).

终值定理：如果 (z−1)X(z) 的极点在单位圆内，则

x[\infty ]=\lim _{z\to 1}(z-1)X(z).

常见的Z变换对表

这里：

u:n\mapsto u[n]={\begin{cases}1,&n\geq 0\\0,&n<0\end{cases}}

是单位阶跃函数而

\delta :n\mapsto \delta [n]={\begin{cases}1,&n=0\\0,&n\neq 0\end{cases}}

是离散时间单位冲激函数。两者通常都不认为是真正的函数，但由于它们的不连续性把它们看成是分布（它们在 n = 0 处的值通常无关紧要，除非在处理离散时间的时候，它们会变成衰减离散级数；在本章节中对连续和离散时间域，都在 n = 0 处取 1，否则不能使用下表中收敛域一栏的内容）。同时列出两个“函数”，使得（在连续时间域）单位阶跃函数是单位冲激函数的积分，或（在离散时间域）单位阶跃函数是单位冲激函数的求和，因此要令他们的值在 n = 0 处为 1。

	信号， $x[n]$	Z变换， $X(z)$	ROC
1	$\delta [n]$	1	所有 z
2	$\delta [n-n_{0}]$	$z^{-n_{0}}$	$z\neq 0$
3	$u[n]\,$	${\frac {1}{1-z^{-1}}}$	$\|z\|>1$
4	$e^{-\alpha n}u[n]$	$1 \over 1-e^{-\alpha }z^{-1}$	$\|z\|>e^{-\alpha }\,$
5	$-u[-n-1]$	${\frac {1}{1-z^{-1}}}$	$\|z\|<1$
6	$nu[n]$	${\frac {z^{-1}}{(1-z^{-1})^{2}}}$	$\|z\|>1$
7	$-nu[-n-1]\,$	${\frac {z^{-1}}{(1-z^{-1})^{2}}}$	$\|z\|<1$
8	$n^{2}u[n]$	${\frac {z^{-1}(1+z^{-1})}{(1-z^{-1})^{3}}}$	$\|z\|>1\,$
9	$-n^{2}u[-n-1]\,$	${\frac {z^{-1}(1+z^{-1})}{(1-z^{-1})^{3}}}$	$\|z\|<1\,$
10	$n^{3}u[n]$	${\frac {z^{-1}(1+4z^{-1}+z^{-2})}{(1-z^{-1})^{4}}}$	$\|z\|>1\,$
11	$-n^{3}u[-n-1]$	${\frac {z^{-1}(1+4z^{-1}+z^{-2})}{(1-z^{-1})^{4}}}$	$\|z\|<1\,$
12	$a^{n}u[n]$	${\frac {1}{1-az^{-1}}}$	$\|z\|>\|a\|$
13	$-a^{n}u[-n-1]$	${\frac {1}{1-az^{-1}}}$	$\|z\|<\|a\|$
14	$na^{n}u[n]$	${\frac {az^{-1}}{(1-az^{-1})^{2}}}$	$\|z\|>\|a\|$
15	$-na^{n}u[-n-1]$	${\frac {az^{-1}}{(1-az^{-1})^{2}}}$	$\|z\|<\|a\|$
16	$n^{2}a^{n}u[n]$	${\frac {az^{-1}(1+az^{-1})}{(1-az^{-1})^{3}}}$	$\|z\|>\|a\|$
17	$-n^{2}a^{n}u[-n-1]$	${\frac {az^{-1}(1+az^{-1})}{(1-az^{-1})^{3}}}$	$\|z\|<\|a\|$
18	$\cos(\omega _{0}n)u[n]$	${\frac {1-z^{-1}\cos(\omega _{0})}{1-2z^{-1}\cos(\omega _{0})+z^{-2}}}$	$\|z\|>1$
19	$\sin(\omega _{0}n)u[n]$	${\frac {z^{-1}\sin(\omega _{0})}{1-2z^{-1}\cos(\omega _{0})+z^{-2}}}$	$\|z\|>1$
20	$a^{n}\cos(\omega _{0}n)u[n]$	${\frac {1-az^{-1}\cos(\omega _{0})}{1-2az^{-1}\cos(\omega _{0})+a^{2}z^{-2}}}$	$\|z\|>\|a\|$
21	$a^{n}\sin(\omega _{0}n)u[n]$	${\frac {az^{-1}\sin(\omega _{0})}{1-2az^{-1}\cos(\omega _{0})+a^{2}z^{-2}}}$	$\|z\|>\|a\|$

与傅里叶级数和傅里叶变换的关系

对于区域 |z|=1（称为单位圆）内的 z 值，我们可以通过定义 z=e^jω 来用单一实变量的函数来表示该变换。于是双边变换就简化为了傅里叶级数：

\sum _{n=-\infty }^{\infty }x[n]\ z^{-n}=\sum _{n=-\infty }^{\infty }x[n]\ e^{-j\omega n},

(Eq.1)

也被称作 x[n] 序列的离散时间傅里叶变换（DTFT）。这个以 2π 为周期的函数是傅里叶变换的周期性求和，这使得它成为广泛使用的分析工具。要理解这一点，令 X(f) 为任意函数 x(t) 的傅里叶变换，该函数以某个间隔 T 采样就与 x[n] 序列相等。于是 x[n] 序列的DTFT可以写作：

\underbrace {\sum _{n=-\infty }^{\infty }\overbrace {x(nT)} ^{x[n]}\ e^{-j2\pi fnT}} _{\text{DTFT}}={\frac {1}{T}}\sum _{k=-\infty }^{\infty }X(f-k/T).

若T的單位是秒， $\textstyle f$ 的單位即為赫兹。比較兩個數列可得 $\textstyle \omega =2\pi fT$ 為标准化频率，單位是radians per sample。數值ω=2π對應 $\textstyle f={\frac {1}{T}}$ Hz. ，而且在替換 $\textstyle f={\frac {\omega }{2\pi T}},$ 後， Eq.1可以表示為傅里叶变换X(•):

\sum _{n=-\infty }^{\infty }x[n]\ e^{-j\omega n}={\frac {1}{T}}\sum _{k=-\infty }^{\infty }\underbrace {X\left({\tfrac {\omega }{2\pi T}}-{\tfrac {k}{T}}\right)} _{X\left({\frac {\omega -2\pi k}{2\pi T}}\right)}.

若數列x(nT)表示线性时不变系统的冲激响应，這些函數也稱為频率响应，當x(nT)是週期性數列，其DTFT在一或多個共振頻率發散，在其他頻率均為零。這一般會用在共振頻率，振幅可變的狄拉克δ函数表示。因為其週期性，只會有有限個振幅，可以用較簡單許多的离散傅里叶变换來計算。（參照離散傅立葉變換#周期性）

和拉氏变換的關係

双线性变换

双线性变换可以用在連續時間濾波器（用拉氏域表示）和離散時間濾波器（用Z域表示）之間的轉換，其轉換關係如下：

s={\frac {2}{T}}{\frac {(z-1)}{(z+1)}}

將一個拉氏域的函數 $H(s)$ 轉換為Z域下的 $H(z)$ ，或是

z={\frac {2+sT}{2-sT}}

從Z域轉換到拉氏域。藉由双线性变换，複數的s平面（拉氏变換）可以映射到複數的z平面（Z轉換）。這個轉換是非線性的，可以將S平面的整個jΩ軸映射到Z平面的单位圆內。因此，傅立葉變換（在jΩ axis計算的拉氏變換）變成離散時間傅立葉變換，前提是假設其傅立葉變換存在，也就是拉氏变換的收斂區域包括jΩ軸。

线性常系数差分方程

线性常系数差分（LCCD）方程是基于自回归滑动平均的线性系统表达形式。

\sum _{p=0}^{N}y[n-p]\alpha _{p}=\sum _{q=0}^{M}x[n-q]\beta _{q}

上面等式两边可以同时除以 α₀，如果非零，正规化 α₀ = 1，LCCD方程可以写成

y[n]=\sum _{q=0}^{M}x[n-q]\beta _{q}-\sum _{p=1}^{N}y[n-p]\alpha _{p}.

LCCD方程的这种形式有利于更加明确“当前”输出 y[n] 是过去输出 y[n−p]、当前输入 x[n] 与之前输入 x[n−q] 的一个函数。

传递函数

对上述方程去Z变换（使用线性和时移法则）得到

Y(z)\sum _{p=0}^{N}z^{-p}\alpha _{p}=X(z)\sum _{q=0}^{M}z^{-q}\beta _{q}

整理结果

H(z)={\frac {Y(z)}{X(z)}}={\frac {\sum _{q=0}^{M}z^{-q}\beta _{q}}{\sum _{p=0}^{N}z^{-p}\alpha _{p}}}={\frac {\beta _{0}+z^{-1}\beta _{1}+z^{-2}\beta _{2}+\cdots +z^{-M}\beta _{M}}{\alpha _{0}+z^{-1}\alpha _{1}+z^{-2}\alpha _{2}+\cdots +z^{-N}\alpha _{N}}}.

零点和极点

由代数基本定理得知分子有 M 个根（对应于 H 的零点）和分母有 N 个根（对应于极点）。用极点和零点重新整理传递函数为

H(z)={\frac {(1-q_{1}z^{-1})(1-q_{2}z^{-1})\cdots (1-q_{M}z^{-1})}{(1-p_{1}z^{-1})(1-p_{2}z^{-1})\cdots (1-p_{N}z^{-1})}}

其中 q_k 为 k 阶零点，p_k 为 k 阶极点。零点和极点通常是复数，当在复平面（z平面）作图时称为零极点图。

此外，在 z = 0 和 z = ∞ 也可能存在零点和极点。如果我们把这些极点和零点以及高阶零点和极点考虑在内的話，零点和极点的数目总会相等。

通过对分母因式分解，可以使用部分分式分解可以转换回时域。这样做会导出系统的冲激响应和线性常系数差分方程。

输出响应

如果一个系统 H(z) 由信号 X(z) 驱动，那么输出为 Y(z) = H(z)X(z)。通过对 Y(z) 部分分式分解并取逆Z变换可以得到输出 y[n]。在实际运用中，在分式分解 ${\frac {Y(z)}{z}}$ 之后再乘 z 产生 Y(z) 的一个形式（含有很容易计算逆Z变换的项）往往很有用。

参见

高级Z变换
双线性变换
差分方程（遞迴關係式）
离散卷积
离散时间傅里叶变换
有限脉冲响应
形式幂级数
拉普拉斯变换
洛朗级数
概率母函数
星标变换
Zak变换
ζ函数正规化

参考文献

E. R. Kanasewich. 3rd. University of Alberta. 1981: 185–186. ISBN 978-0-88864-074-1.
J. R. Ragazzini and L. A. Zadeh. . Trans. Am. Inst. Elec. Eng. 1952, 71 (II): 225–234.
Cornelius T. Leondes. . Academic Press. 1996: 123. ISBN 978-0-12-012779-5.
Eliahu Ibrahim Jury. . John Wiley & Sons. 1958.
Eliahu Ibrahim Jury. . Krieger Pub Co. 1973. ISBN 0-88275-122-0.
Eliahu Ibrahim Jury. . John Wiley & Sons. 1964: 1.
Enders A. Robinson, Sven Treitel. . SEG Books. 2008: 163, 375–376. ISBN 9781560801481.
E. R. Kanasewich. . University of Alberta. 1981: 186, 249. ISBN 9780888640741.

延伸阅读

Refaat El Attar, Lecture notes on Z-Transform, Lulu Press, Morrisville NC, 2005. ISBN 978-1-4116-1979-1.
Ogata, Katsuhiko, Discrete Time Control Systems 2nd Ed, Prentice-Hall Inc, 1995, 1987. ISBN 978-0-13-034281-2.
Alan V. Oppenheim and Ronald W. Schafer (1999). Discrete-Time Signal Processing, 2nd Edition, Prentice Hall Signal Processing Series. ISBN 978-0-13-754920-7.

外部链接

Hazewinkel, Michiel (编), , , Springer, 2001, ISBN 978-1-55608-010-4
Z-Transform table of some common Laplace transforms （页面存档备份，存于）
Mathworld's entry on the Z-transform （页面存档备份，存于）
Z-Transform threads in Comp.DSP （页面存档备份，存于）
Z-Transform Module by John H. Mathews
A graphic of the relationship between Laplace transform s-plane to Z-plane of the Z transform （页面存档备份，存于）

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] E. R. Kanasewich. 3rd. University of Alberta. 1981: 185–186. ISBN 978-0-88864-074-1.

[2] J. R. Ragazzini and L. A. Zadeh. . Trans. Am. Inst. Elec. Eng. 1952, 71 (II): 225–234.

[3] Cornelius T. Leondes. . Academic Press. 1996: 123. ISBN 978-0-12-012779-5.

[4] Eliahu Ibrahim Jury. . John Wiley & Sons. 1958.

[5] Eliahu Ibrahim Jury. . Krieger Pub Co. 1973. ISBN 0-88275-122-0.

[6] Eliahu Ibrahim Jury. . John Wiley & Sons. 1964: 1.

[robinson-7] Enders A. Robinson, Sven Treitel. . SEG Books. 2008: 163, 375–376. ISBN 9781560801481.

[kanasewich-8] E. R. Kanasewich. . University of Alberta. 1981: 186, 249. ISBN 9780888640741.