| Elongated octahedron | |
|---|---|
 | |
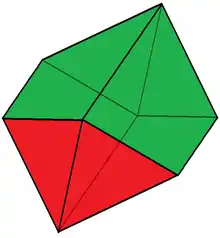| Faces | 4 triangles 4 isosceles trapezoids |
| Edges | 14 |
| Vertices | 8 |
| Vertex configuration | 4 (32.42) 4 (3.42) |
| Symmetry group | D2h, [2,2], (*222), order 8 |
| Dual polyhedron | self-dual |
| Properties | convex |
| Net | |
 | |
| Deltahedral hexadecahedron | |
|---|---|
 | |
| Faces | 16 triangles |
| Edges | 24 |
| Vertices | 10 |
| Vertex configuration | 4 (34) 4 (35) 2 (36) |
| Symmetry group | D2h, [2,2], (*222), order 8 |
| Properties | deltahedron |
| Net | |
 | |
In geometry, an elongated octahedron is a polyhedron with 8 faces (4 triangular, 4 isosceles trapezoidal), 14 edges, and 8 vertices.
As a deltahedral hexadecahedron
A related construction is a hexadecahedron, 16 triangular faces, 24 edges, and 10 vertices. Starting with the regular octahedron, it is elongated along one axes, adding 8 new triangles. It has 2 sets of 3 coplanar equilateral triangles (each forming a half-hexagon), and thus is not a Johnson solid.
If the sets of coplanar triangles are considered a single isosceles trapezoidal face (a triamond), it has 8 vertices, 14 edges, and 8 faces - 4 triangles 
and 4 triamonds 
. This construction has been called a triamond stretched octahedron.[1]
As a folded hexahedron
Another interpretation can represent this solid as a hexahedron, by considering pairs of trapezoids as a folded regular hexagon. It will have 6 faces (4 triangles, and 2 hexagons), 12 edges, and 8 vertices.
It could also be seen as a folded tetrahedron also seeing pairs of end triangles as a folded rhombus. It would have 8 vertices, 10 edges, and 4 faces.
Cartesian coordinates
The Cartesian coordinates of the 8 vertices of an elongated octahedron, elongated in the x-axis, with edge length 2 are:
- ( ±1, 0, ±2 )
- ( ±2, ±1, 0 ).
The 2 extra vertices of the deltahedral variation are:
- ( 0, ±1, 0 ).
Related polyhedra and honeycombs
In the special case, where the trapezoid faces are squares or rectangles, the pairs of triangles becoming coplanar and the polyhedron's geometry is more specifically a right rhombic prism.
This polyhedron has a highest symmetry as D2h symmetry, order 8, representing 3 orthogonal mirrors. Removing one mirror between the pairs of triangles divides the polyhedron into two identical wedges, giving the names octahedral wedge, or double wedge. The half-model has 8 triangles and 2 squares.
It can also be seen as the augmentation of 2 octahedrons, sharing a common edge, with 2 tetrahedrons filling in the gaps. This represents a section of a tetrahedral-octahedral honeycomb. The elongated octahedron can thus be used with the tetrahedron as a space-filling honeycomb.
See also
References
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. p.172 tetrahedra-octahedral packing
- H. Martyn Cundy Deltahedra. Math. Gaz. 36, 263-266, Dec 1952.
- H. Martyn Cundy and A. Rollett. "Deltahedra". §3.11 in Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., pp. 142–144, 1989.
- Charles W. Trigg An Infinite Class of Deltahedra, Mathematics Magazine, Vol. 51, No. 1 (Jan., 1978), pp. 55–57
- Johnson, Norman W. (1966). "Convex Solids with Regular Faces". Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. ISSN 0008-414X. Zbl 0132.14603. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
- Zalgaller, Victor A. (1969). Convex Polyhedra with Regular Faces. Consultants Bureau. Zbl 0177.24802. No ISBN. The first proof that there are only 92 Johnson solids: see also Zalgaller, Victor A. (1967). "Convex Polyhedra with Regular Faces". Zap. Nauchn. Semin. Leningr. Otd. Mat. Inst. Steklova (in Russian). 2: 1–221. ISSN 0373-2703. Zbl 0165.56302.