In mathematics, Euclidean relations are a class of binary relations that formalize "Axiom 1" in Euclid's Elements: "Magnitudes which are equal to the same are equal to each other."
Definition
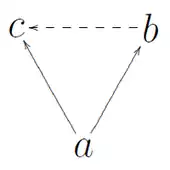
Right Euclidean property: solid and dashed arrows indicate antecedents and consequents, respectively.
A binary relation R on a set X is Euclidean (sometimes called right Euclidean) if it satisfies the following: for every a, b, c in X, if a is related to b and c, then b is related to c.[1] To write this in predicate logic:
Dually, a relation R on X is left Euclidean if for every a, b, c in X, if b is related to a and c is related to a, then b is related to c:
Properties
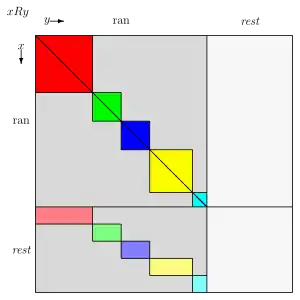
Schematized right Euclidean relation according to property 10. Deeply-colored squares indicate the equivalence classes of R′. Pale-colored rectangles indicate possible relationships of elements in X\ran(R). In these rectangles, relationships may, or may not, hold.
- Due to the commutativity of ∧ in the definition's antecedent, aRb ∧ aRc even implies bRc ∧ cRb when R is right Euclidean. Similarly, bRa ∧ cRa implies bRc ∧ cRb when R is left Euclidean.
- The property of being Euclidean is different from transitivity. For example, ≤ is transitive, but not right Euclidean,[2] while xRy defined by 0 ≤ x ≤ y + 1 ≤ 2 is not transitive,[3] but right Euclidean on natural numbers.
- For symmetric relations, transitivity, right Euclideanness, and left Euclideanness all coincide. However, a non-symmetric relation can also be both transitive and right Euclidean, for example, xRy defined by y=0.
- A relation that is both right Euclidean and reflexive is also symmetric and therefore an equivalence relation.[1][4] Similarly, each left Euclidean and reflexive relation is an equivalence.
- The range of a right Euclidean relation is always a subset[5] of its domain. The restriction of a right Euclidean relation to its range is always reflexive,[6] and therefore an equivalence. Similarly, the domain of a left Euclidean relation is a subset of its range, and the restriction of a left Euclidean relation to its domain is an equivalence. Therefore, a right Euclidean relation on X that is also right total (respectively a left Euclidean relation on X that is also left total) is an equivalence, since its range (respectively its domain) is X.[7]
- A relation R is both left and right Euclidean, if, and only if, the domain and the range set of R agree, and R is an equivalence relation on that set.[8]
- A right Euclidean relation is always quasitransitive,[9] as is a left Euclidean relation.[10]
- A connected right Euclidean relation is always transitive;[11] and so is a connected left Euclidean relation.[12]
- If X has at least 3 elements, a connected right Euclidean relation R on X cannot be antisymmetric,[13] and neither can a connected left Euclidean relation on X.[14] On the 2-element set X = { 0, 1 }, e.g. the relation xRy defined by y=1 is connected, right Euclidean, and antisymmetric, and xRy defined by x=1 is connected, left Euclidean, and antisymmetric.
- A relation R on a set X is right Euclidean if, and only if, the restriction R′ := R|ran(R) is an equivalence and for each x in X\ran(R), all elements to which x is related under R are equivalent under R′.[15] Similarly, R on X is left Euclidean if, and only if, R′ := R|dom(R) is an equivalence and for each x in X\dom(R), all elements that are related to x under R are equivalent under R′.
- A left Euclidean relation is left-unique if, and only if, it is antisymmetric. Similarly, a right Euclidean relation is right unique if, and only if, it is anti-symmetric.
- A left Euclidean and left unique relation is vacuously transitive, and so is a right Euclidean and right unique relation.
- A left Euclidean relation is left quasi-reflexive. For left-unique relations, the converse also holds. Dually, each right Euclidean relation is right quasi-reflexive, and each right unique and right quasi-reflexive relation is right Euclidean.[16]
References
- 1 2 Fagin, Ronald (2003), Reasoning About Knowledge, MIT Press, p. 60, ISBN 978-0-262-56200-3.
- ↑ e.g. 0 ≤ 2 and 0 ≤ 1, but not 2 ≤ 1
- ↑ e.g. 2R1 and 1R0, but not 2R0
- ↑ xRy and xRx implies yRx.
- ↑ Equality of domain and range isn't necessary: the relation xRy defined by y=min{x,2} is right Euclidean on the natural numbers, and its range, {0,1,2}, is a proper subset of its domain of the natural numbers.
- ↑ If y is in the range of R, then xRy ∧ xRy implies yRy, for some suitable x. This also proves that y is in the domain of R.
- ↑ Buck, Charles (1967), "An Alternative Definition for Equivalence Relations", The Mathematics Teacher, 60: 124-125.
- ↑ The only if direction follows from the previous paragraph. — For the if direction, assume aRb and aRc, then a,b,c are members of the domain and range of R, hence bRc by symmetry and transitivity; left Euclideanness of R follows similarly.
- ↑ If xRy ∧ ¬yRx ∧ yRz ∧ ¬zRy holds, then both y and z are in the range of R. Since R is an equivalence on that set, yRz implies zRy. Hence the antecedent of the quasi-transitivity definition formula cannot be satisfied.
- ↑ A similar argument applies, observing that x,y are in the domain of R.
- ↑ If xRy ∧ yRz holds, then y and z are in the range of R. Since R is connected, xRz or zRx or x=z holds. In case 1, nothing remains to be shown. In cases 2 and 3, also x is in the range. Hence, xRz follows from the symmetry and reflexivity of R on its range, respectively.
- ↑ Similar, using that x, y are in the domain of R.
- ↑ Since R is connected, at least two distinct elements x,y are in its range, and xRy ∨ yRx holds. Since R is symmetric on its range, even xRy ∧ yRx holds. This contradicts the antisymmetry property.
- ↑ By a similar argument, using the domain of R.
- ↑ Only if: R′ is an equivalence as shown above. If x∈X\ran(R) and xR′y1 and xR′y2, then y1Ry2 by right Euclideaness, hence y1R′y2. — If: if xRy ∧ xRz holds, then y,z∈ran(R). In case also x∈ran(R), even xR′y ∧ xR′z holds, hence yR′z by symmetry and transitivity of R′, hence yRz. In case x∈X\ran(R), the elements y and z must be equivalent under R′ by assumption, hence also yRz.
- ↑ Jochen Burghardt (Nov 2018). Simple Laws about Nonprominent Properties of Binary Relations (Technical Report). arXiv:1806.05036v2. Lemma 44-46.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.