In mathematical physics and probability and statistics, the Gaussian q-distribution is a family of probability distributions that includes, as limiting cases, the uniform distribution and the normal (Gaussian) distribution. It was introduced by Diaz and Teruel. It is a q-analog of the Gaussian or normal distribution.

The distribution is symmetric about zero and is bounded, except for the limiting case of the normal distribution. The limiting uniform distribution is on the range -1 to +1.

Definition

The Gaussian q-density.

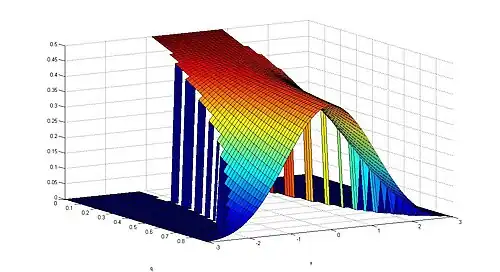
Let q be a real number in the interval [0, 1). The probability density function of the Gaussian q-distribution is given by

${\displaystyle s_{q}(x)={\begin{cases}0&{\text{if }}x<-\nu \\{\frac {1}{c(q)}}E_{q^{2}}^{\frac {-q^{2}x^{2}}{[2]_{q}}}&{\text{if }}-\nu \leq x\leq \nu \\0&{\mbox{if }}x>\nu .\end{cases}}}$

where

${\displaystyle \nu =\nu (q)={\frac {1}{\sqrt {1-q}}},}$

${\displaystyle c(q)=2(1-q)^{1/2}\sum _{m=0}^{\infty }{\frac {(-1)^{m}q^{m(m+1)}}{(1-q^{2m+1})(1-q^{2})_{q^{2}}^{m}}}.}$

The q-analogue [t]_q of the real number ${\displaystyle t}$ is given by

${\displaystyle [t]_{q}={\frac {q^{t}-1}{q-1}}.}$

The q-analogue of the exponential function is the q-exponential, E^x
_q, which is given by

${\displaystyle E_{q}^{x}=\sum _{j=0}^{\infty }q^{j(j-1)/2}{\frac {x^{j}}{[j]!}}}$

where the q-analogue of the factorial is the q-factorial, [n]_q!, which is in turn given by

${\displaystyle [n]_{q}!=[n]_{q}[n-1]_{q}\cdots [2]_{q}\,}$

for an integer n > 2 and [1]_q! = [0]_q! = 1.

The Cumulative Gaussian q-distribution.

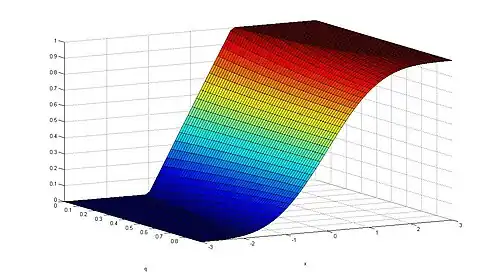
The cumulative distribution function of the Gaussian q-distribution is given by

${\displaystyle G_{q}(x)={\begin{cases}0&{\text{if }}x<-\nu \\[12pt]\displaystyle {\frac {1}{c(q)}}\int _{-\nu }^{x}E_{q^{2}}^{-q^{2}t^{2}/[2]}\,d_{q}t&{\text{if }}-\nu \leq x\leq \nu \\[12pt]1&{\text{if }}x>\nu \end{cases}}}$

where the integration symbol denotes the Jackson integral.

The function G_q is given explicitly by

${\displaystyle G_{q}(x)={\begin{cases}0&{\text{if }}x<-\nu ,\\\displaystyle {\frac {1}{2}}+{\frac {1-q}{c(q)}}\sum _{n=0}^{\infty }{\frac {q^{n(n+1)}(q-1)^{n}}{(1-q^{2n+1})(1-q^{2})_{q^{2}}^{n}}}x^{2n+1}&{\text{if }}-\nu \leq x\leq \nu \\1&{\text{if}}\ x>\nu \end{cases}}}$

where

${\displaystyle (a+b)_{q}^{n}=\prod _{i=0}^{n-1}(a+q^{i}b).}$

Moments

The moments of the Gaussian q-distribution are given by

${\displaystyle {\frac {1}{c(q)}}\int _{-\nu }^{\nu }E_{q^{2}}^{-q^{2}x^{2}/[2]}\,x^{2n}\,d_{q}x=[2n-1]!!,}$

${\displaystyle {\frac {1}{c(q)}}\int _{-\nu }^{\nu }E_{q^{2}}^{-q^{2}x^{2}/[2]}\,x^{2n+1}\,d_{q}x=0,}$

where the symbol [2n − 1]!! is the q-analogue of the double factorial given by

${\displaystyle [2n-1][2n-3]\cdots [1]=[2n-1]!!.\,}$

See also

• Q-Gaussian process

References

• Díaz, R.; Pariguan, E. (2009). "On the Gaussian q-distribution". Journal of Mathematical Analysis and Applications. 358: 1–9. arXiv:0807.1918. doi:10.1016/j.jmaa.2009.04.046. S2CID 115175228.
• Diaz, R.; Teruel, C. (2005). "q,k-Generalized Gamma and Beta Functions" (PDF). Journal of Nonlinear Mathematical Physics. 12 (1): 118–134. arXiv:math/0405402. Bibcode:2005JNMP...12..118D. doi:10.2991/jnmp.2005.12.1.10. S2CID 73643153.
• van Leeuwen, H.; Maassen, H. (1995). "A q deformation of the Gauss distribution" (PDF). Journal of Mathematical Physics. 36 (9): 4743. Bibcode:1995JMP....36.4743V. CiteSeerX 10.1.1.24.6957. doi:10.1063/1.530917. hdl:2066/141604. S2CID 13934946.
• Exton, H. (1983), q-Hypergeometric Functions and Applications, New York: Halstead Press, Chichester: Ellis Horwood, 1983, ISBN 0853124914, ISBN 0470274530, ISBN 978-0470274538