The Hanoi graph ${\displaystyle H_{3}^{7}}$

In graph theory and recreational mathematics, the Hanoi graphs are undirected graphs whose vertices represent the possible states of the Tower of Hanoi puzzle, and whose edges represent allowable moves between pairs of states.

Construction

The Hanoi graph ${\displaystyle H_{3}^{5}}$ (black discs) derived from the odd values in Pascal's triangle

The puzzle consists of a set of disks of different sizes, placed in increasing order of size on a fixed set of towers. The Hanoi graph for a puzzle with ${\displaystyle n}$ disks on ${\displaystyle k}$ towers is denoted ${\displaystyle H_{k}^{n}}$.^[1][2] Each state of the puzzle is determined by the choice of one tower for each disk, so the graph has ${\displaystyle k^{n}}$ vertices.^[2]

In the moves of the puzzle, the smallest disk on one tower is moved either to an unoccupied tower or to a tower whose smallest disk is larger. If there are ${\displaystyle u}$ unoccupied towers, the number of allowable moves is

${\displaystyle {\binom {k}{2}}-{\binom {u}{2}},}$

which ranges from a maximum of ${\displaystyle {\tbinom {k}{2}}}$ (when ${\displaystyle u}$ is zero or one and ${\displaystyle {\tbinom {u}{2}}}$ is zero) to ${\displaystyle k-1}$ (when all disks are on one tower and ${\displaystyle u}$ is ${\displaystyle k-1}$). Therefore, the degrees of the vertices in the Hanoi graph range from a maximum of ${\displaystyle {\tbinom {k}{2}}}$ to a minimum of ${\displaystyle k-1}$. The total number of edges is^[3]

${\displaystyle {\frac {1}{2}}{\binom {k}{2}}{\bigl (}k^{n}-(k-2)^{n}{\bigr )}.}$

For ${\displaystyle k=0}$ (no disks) there is only one state of the puzzle and one vertex of the graph. For ${\displaystyle k>0}$, the Hanoi graph ${\displaystyle H_{k}^{n}}$ can be decomposed into ${\displaystyle k}$ copies of the smaller Hanoi graph ${\displaystyle H_{k}^{n-1}}$, one for each placement of the largest disk. These copies are connected to each other only at states where the largest disk is free to move: it is the only disk in its tower, and some other tower is unoccupied.^[4]

General properties

${\displaystyle H_{3}^{3}}$ with 12 edges deleted to yield a Hamiltonian cycle

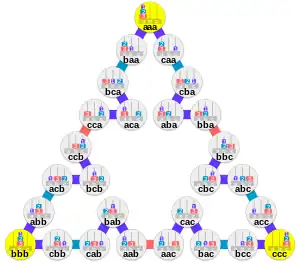
Every Hanoi graph contains a Hamiltonian cycle.^[5]

The Hanoi graph ${\displaystyle H_{k}^{1}}$ is a complete graph on ${\displaystyle k}$ vertices. Because they contain complete graphs, all larger Hanoi graphs ${\displaystyle H_{k}^{n}}$ require at least ${\displaystyle k}$ colors in any graph coloring. They may be colored with exactly ${\displaystyle k}$ colors by summing the indexes of the towers containing each disk, and using the sum modulo ${\displaystyle k}$ as the color.^[3]

Three towers

A particular case of the Hanoi graphs that has been well studied since the work of Scorer, Grundy & Smith (1944)^[1][6] is the case of the three-tower Hanoi graphs, ${\displaystyle H_{3}^{n}}$. These graphs have 3ⁿ vertices (OEIS: A000244) and 3(3ⁿ − 1)/2 edges (OEIS: A029858).^[7] They are penny graphs (the contact graphs of non-overlapping unit disks in the plane), with an arrangement of disks that resembles the Sierpinski triangle. One way of constructing this arrangement is to arrange the numbers of Pascal's triangle on the points of a hexagonal lattice, with unit spacing, and place a unit disk on each point whose number is odd. The diameter of these graphs, and the length of the solution to the standard form of the Tower of Hanoi puzzle (in which the disks all start on one tower and must all move to one other tower) is ${\displaystyle 2^{n}-1}$.^[2]

More than three towers

For ${\displaystyle k>3}$, the structure of the Hanoi graphs is not as well understood, and the diameter of these graphs is unknown.^[2] When ${\displaystyle k>4}$ and ${\displaystyle n>0}$ or when ${\displaystyle k=4}$ and ${\displaystyle n>2}$, these graphs are nonplanar.^[5]

See also

• Sierpinski triangle

References