11 pennies, forming a penny graph with 11 vertices and 19 edges
The Hanoi graph as a penny graph (the contact graph of the black disks)

In geometric graph theory, a penny graph is a contact graph of unit circles. It is formed from a collection of unit circles that do not cross each other, by creating a vertex for each circle and an edge for every pair of tangent circles.[1] The circles can be represented physically by pennies, arranged without overlapping on a flat surface, with a vertex for each penny and an edge for each two pennies that touch.

Penny graphs have also been called unit coin graphs,[2] because they are the coin graphs formed from unit circles.[1] If each vertex is represented by a point at the center of its circle, then two vertices will be adjacent if and only if their distance is the minimum distance among all pairs of vertices. Therefore, penny graphs have also been called minimum-distance graphs,[3] smallest-distance graphs,[4] or closest-pairs graphs.[5] Similarly, in a mutual nearest neighbor graph that links pairs of points in the plane that are each other's nearest neighbors, each connected component is a penny graph, although edges in different components may have different lengths.[6]

Every penny graph is a unit disk graph and a matchstick graph. Like planar graphs more generally, they obey the four color theorem, but this theorem is easier to prove for penny graphs. Testing whether a graph is a penny graph, or finding its maximum independent set, is NP-hard; however, both upper and lower bounds are known for the size of the maximum independent set, higher than the bounds that are possible for arbitrary planar graphs.

Properties

Number of edges

Every vertex in a penny graph has at most six neighboring vertices; here the number six is the kissing number for circles in the plane. However, the pennies on the boundary of the convex hull have fewer neighbors. Counting more precisely this reduction in neighbors for boundary pennies leads to a precise bound on the number of edges in any penny graph: a penny graph with n vertices has at most

edges. Some penny graphs, formed by arranging the pennies in a triangular grid, have exactly this number of edges.[7][8][9]

Unsolved problem in mathematics:

What is the maximum number of edges in a triangle-free penny graph?

(more unsolved problems in mathematics)

By arranging the pennies in a square grid, or in the form of certain squaregraphs, one can form triangle-free penny graphs whose number of edges is at least

and in any triangle-free penny graph the number of edges is at most[10]

Swanepoel conjectured that the bound is tight.[11] Proving this, or finding a better bound, remains open.

Coloring

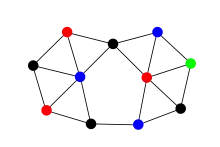
An optimal coloring of the 11-vertex penny graph shown above requires four colors

Every penny graph contains a vertex with at most three neighbors. For instance, such a vertex can be found at one of the corners of the convex hull of the circle centers. Therefore, penny graphs have degeneracy at most three. Based on this, one can prove that their graph colorings require at most four colors, much more easily than the proof of the more general four-color theorem.[12] However, despite their restricted structure, there exist penny graphs that do still require four colors.[13]

A triangle-free penny graph with the property that all the pennies on the convex hull touch at least three other pennies

Analogously, the degeneracy of every triangle-free penny graph is at most two. Every such graph contains a vertex with at most two neighbors, even though it is not always possible to find this vertex on the convex hull. Based on this, one can prove that they require at most three colors, more easily than the proof of the more general Grötzsch's theorem that triangle-free planar graphs are 3-colorable.[10]

Independent sets

A maximum independent set in a penny graph is a subset of the pennies, no two of which touch each other. Finding maximum independent sets is NP-hard for arbitrary graphs, and remains NP-hard on penny graphs.[2] It is an instance of the maximum disjoint set problem, in which one must find large subsets of non-overlapping regions of the plane. However, as with planar graphs more generally, Baker's technique provides a polynomial-time approximation scheme for this problem.[14]

Unsolved problem in mathematics:

What is the largest such that every -vertex penny graph has an independent set of size ?

(more unsolved problems in mathematics)

In 1983, Paul Erdős asked for the largest number c such that every n-vertex penny graph has an independent set of at least cn vertices.[15] That is, if we place n pennies on a flat surface, there should be a subset of cn of the pennies that do not touch each other. By the four-color theorem, c ≥ 1/4, and the improved bound c ≥ 8/31 ≈ 0.258 was proven by Swanepoel.[16] In the other direction, Pach and Tóth proved that c ≤ 5/16 = 0.3125.[15] As of 2013, these remained the best bounds known for this problem.[4][17]

Computational complexity

Constructing a penny graph from the locations of its n circles can be performed as an instance of the closest pair of points problem, taking worst-case time O(n log n)[5] or (with randomized time and with the use of the floor function) expected time O(n).[18] An alternative method with the same worst-case time is to construct the Delaunay triangulation or nearest neighbor graph of the circle centers (both of which contain the penny graph as a subgraph)[5] and then test which edges correspond to circle tangencies.

However, if a graph is given without geometric positions for its vertices, then testing whether it can be represented as a penny graph is NP-hard.[6] It remains NP-hard even when the given graph is a tree.[19] Similarly, testing whether a graph can be represented as a three-dimensional mutual nearest neighbor graph is also NP-hard.[20]

It is possible to perform some computational tasks on directed penny graphs, such as testing whether one vertex can reach another, in polynomial time and substantially less than linear space, given an input representing its circles in a form allowing basic computational tasks such as testing adjacency and finding intersections of the circles with axis-parallel lines.[21]

Penny graphs are a special case of the coin graphs (graphs that can be represented by tangencies of non-crossing circles of arbitrary radii).[1] Because the coin graphs are the same as the planar graphs,[22] all penny graphs are planar. The penny graphs are also unit disk graphs (the intersection graphs of unit circles),[2] unit distance graphs (graphs that can be drawn with all edges having equal lengths, allowing crossings),[23] and matchstick graphs (graphs that can be drawn in the plane with equal-length straight edges and no edge crossings).[24]

References

  1. 1 2 3 Cerioli, Marcia R.; Faria, Luerbio; Ferreira, Talita O.; Protti, Fábio (2011), "A note on maximum independent sets and minimum clique partitions in unit disk graphs and penny graphs: complexity and approximation", RAIRO Theoretical Informatics and Applications, 45 (3): 331–346, doi:10.1051/ita/2011106, MR 2836493
  2. ↑ Csizmadia, G. (1998), "On the independence number of minimum distance graphs", Discrete & Computational Geometry, 20 (2): 179–187, doi:10.1007/PL00009381, MR 1637884
  3. 1 2 Brass, Peter; Moser, William; Pach, János (2005), Research Problems in Discrete Geometry, New York: Springer, p. 228, ISBN 978-0387-23815-9, MR 2163782
  4. 1 2 3 Veltkamp, Remco C. (1994), "2.2.1 Closest pairs", Closed Object Boundaries from Scattered Points, Lecture Notes in Computer Science, vol. 885, Berlin: Springer-Verlag, p. 12, doi:10.1007/3-540-58808-6, ISBN 3-540-58808-6
  5. 1 2 Eades, Peter; Whitesides, Sue (1996), "The logic engine and the realization problem for nearest neighbor graphs", Theoretical Computer Science, 169 (1): 23–37, doi:10.1016/S0304-3975(97)84223-5, MR 1424926
  6. ↑ Harborth, H. (1974), "Lösung zu Problem 664A", Elemente der Mathematik, 29: 14–15. As cited by Swanepoel (2009) and Pach & Agarwal (1995).
  7. ↑ Pach, János; Agarwal, Pankaj K. (1995), Combinatorial Geometry, Wiley-Interscience Series in Discrete Mathematics and Optimization, New York: John Wiley & Sons, Inc., doi:10.1002/9781118033203, ISBN 0-471-58890-3, MR 1354145; see Theorem 13.12, p. 211.
  8. ↑ Kupitz, Y. S. (1994), "On the maximal number of appearances of the minimal distance among n points in the plane", Intuitive Geometry (Szeged, 1991), Colloq. Math. Soc. János Bolyai, vol. 63, North-Holland, pp. 217–244, MR 1383628
  9. 1 2 Eppstein, David (2018), "Edge bounds and degeneracy of triangle-free penny graphs and squaregraphs", Journal of Graph Algorithms and Applications, 22 (3): 483–499, arXiv:1708.05152, doi:10.7155/jgaa.00463, MR 3866392
  10. ↑ Swanepoel, Konrad J. (2009), "Triangle-free minimum distance graphs in the plane" (PDF), Geombinatorics, 19 (1): 28–30, MR 2584434
  11. ↑ Hartsfield, Nora; Ringel, Gerhard (2013), "Problem 8.4.8", Pearls in Graph Theory: A Comprehensive Introduction, Dover Books on Mathematics, Courier Corporation, pp. 177–178, ISBN 9780486315522.
  12. ↑ Gardner, Martin (March 1975), "From rubber ropes to rolling cubes, a miscellany of refreshing problems", Mathematical Games, Scientific American, 232 (3): 112–117, doi:10.1038/scientificamerican0375-112, JSTOR 24949757; see problem 7, "the colored poker chips", p. 114.
  13. ↑ Baker, B. (1994), "Approximation algorithms for NP-complete problems on planar graphs", Journal of the ACM, 41 (1): 153–180, doi:10.1145/174644.174650, S2CID 9706753
  14. 1 2 Pach, János; Tóth, Géza (1996), "On the independence number of coin graphs", Geombinatorics, 6 (1): 30–33, MR 1392795
  15. ↑ Swanepoel, Konrad J. (2002), "Independence numbers of planar contact graphs", Discrete & Computational Geometry, 28 (4): 649–670, arXiv:math/0403023, doi:10.1007/s00454-002-2897-y, MR 1949907; Swanepoel's result strengthens an earlier c ≥ 9/35 ≈ 0.257 bound of Csizmadia (1998).
  16. ↑ Dumitrescu, Adrian; Jiang, Minghui (June 2013), "Computational Geometry Column 56" (PDF), SIGACT News, New York, NY, US: ACM, 44 (2): 80–87, arXiv:cs/9908007, doi:10.1145/2491533.2491550, S2CID 52807205
  17. ↑ Khuller, Samir; Matias, Yossi (1995), "A simple randomized sieve algorithm for the closest-pair problem", Information and Computation, 118 (1): 34–37, doi:10.1006/inco.1995.1049, MR 1329236
  18. ↑ Bowen, Clinton; Durocher, Stephane; Löffler, Maarten; Rounds, Anika; Schulz, André; Tóth, Csaba D. (2015), "Realization of simply connected polygonal linkages and recognition of unit disk contact trees", in Giacomo, Emilio Di; Lubiw, Anna (eds.), Graph Drawing and Network Visualization: 23rd International Symposium, GD 2015, Los Angeles, CA, USA, September 24–26, 2015, Revised Selected Papers, Lecture Notes in Computer Science, vol. 9411, Springer, pp. 447–459, doi:10.1007/978-3-319-27261-0_37
  19. ↑ Kitching, Matthew; Whitesides, Sue (2004), "The Three Dimensional Logic Engine", in Pach, János (ed.), Graph Drawing, 12th International Symposium, GD 2004, New York, NY, USA, September 29 - October 2, 2004, Revised Selected Papers, Lecture Notes in Computer Science, vol. 3383, Springer, pp. 329–339, doi:10.1007/978-3-540-31843-9_33
  20. ↑ Bhore, Sujoy; Jain, Rahul (2021), "Space-efficient algorithms for reachability in directed geometric graphs", in Ahn, Hee-Kap; Sadakane, Kunihiko (eds.), 32nd International Symposium on Algorithms and Computation (ISAAC 2021), Leibniz International Proceedings in Informatics (LIPIcs), vol. 212, Dagstuhl, Germany: Schloss Dagstuhl – Leibniz-Zentrum für Informatik, pp. 63:1–63:17, doi:10.4230/LIPIcs.ISAAC.2021.63, ISBN 978-3-95977-214-3, S2CID 244731943
  21. ↑ Hartsfield & Ringel (2013), Theorem 8.4.2, p. 173.
  22. ↑ Horvat, Boris; Pisanski, Tomaž (2010), "Products of unit distance graphs", Discrete Mathematics, 310 (12): 1783–1792, doi:10.1016/j.disc.2009.11.035, MR 2610282
  23. ↑ Feuilloley, Laurent (May 29, 2019), "Graphs defined by matchsticks, pennies and hinges", Discrete notes
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.