In chemistry and physics, the iron group refers to elements that are in some way related to iron; mostly in period (row) 4 of the periodic table. The term has different meanings in different contexts.

In chemistry, the term is largely obsolete, but it often means iron, cobalt, and nickel, also called the iron triad;[1] or, sometimes, other elements that resemble iron in some chemical aspects.

In astrophysics and nuclear physics, the term is still quite common, and it typically means those three plus chromium and manganese—five elements that are exceptionally abundant, both on Earth and elsewhere in the universe, compared to their neighbors in the periodic table. Titanium and vanadium are also produced in Type Ia supernovae.[2]

General chemistry

In chemistry, "iron group" used to refer to iron and the next two elements in the periodic table, namely cobalt and nickel. These three comprised the "iron triad".[1] They are the top elements of groups 8, 9, and 10 of the periodic table; or the top row of "group VIII" in the old (pre-1990) IUPAC system, or of "group VIIIB" in the CAS system.[3] These three metals (and the three of the platinum group, immediately below them) were set aside from the other elements because they have obvious similarities in their chemistry, but are not obviously related to any of the other groups. The iron group and its alloys exhibit ferromagnetism.

The similarities in chemistry were noted as one of Döbereiner's triads and by Adolph Strecker in 1859.[4] Indeed, Newlands' "octaves" (1865) were harshly criticized for separating iron from cobalt and nickel.[5] Mendeleev stressed that groups of "chemically analogous elements" could have similar atomic weights as well as atomic weights which increase by equal increments, both in his original 1869 paper[6] and his 1889 Faraday Lecture.[7]

Analytical chemistry

In the traditional methods of qualitative inorganic analysis, the iron group consists of those cations which

The main cations in the iron group are iron itself (Fe2+ and Fe3+), aluminium (Al3+) and chromium (Cr3+).[8] If manganese is present in the sample, a small amount of hydrated manganese dioxide is often precipitated with the iron group hydroxides.[8] Less common cations which are precipitated with the iron group include beryllium, titanium, zirconium, vanadium, uranium, thorium and cerium.[9]

Astrophysics

The iron group in astrophysics is the group of elements from chromium to nickel, which are substantially more abundant in the universe than those that come after them – or immediately before them – in order of atomic number.[10] The study of the abundances of iron group elements relative to other elements in stars and supernovae allows the refinement of models of stellar evolution.

Abundances of the chemical elements in the Solar System. The scale of the vertical axis is logarithmic. Hydrogen and helium are most common, from the Big Bang. The next three elements (Li, Be, B) are rare because they are poorly synthesized in the Big Bang and also in stars. The two general trends in the remaining stellar-produced elements are: (1) an alternation of abundance in elements as they have even or odd atomic numbers, and (2) a general decrease in abundance, as elements become heavier. The "iron peak" may be seen in the elements near iron as a secondary effect, increasing relative abundances of elements with nuclei most strongly bound.

The explanation for this relative abundance can be found in the process of nucleosynthesis in certain stars, specifically those of about 8–11 Solar masses. At the end of their lives, once other fuels have been exhausted, such stars can enter a brief phase of "silicon burning".[11] This involves the sequential addition of helium nuclei 4
2He
 (an "alpha process") to the heavier elements present in the star, starting from 28
14Si
:

28
14Si
 		+ 4
2He
 		→ 32
16S
32
16S
 		+ 4
2He
 		→ 36
18Ar
36
18Ar
 		+ 4
2He
 		→ 40
20Ca
40
20Ca
 		+ 4
2He
 		→ 44
22Ti
 [note 1]
44
22Ti
 		+ 4
2He
 		→ 48
24Cr
48
24Cr
 		+ 4
2He
 		→ 52
26Fe
52
26Fe
 		+ 4
2He
 		→ 56
28Ni

All of these nuclear reactions are exothermic: the energy that is released partially offsets the gravitational contraction of the star. However, the series ends at 56
28Ni
, as the next reaction in the series

56
28Ni
 		+ 4
2He
 		→ 60
30Zn

is endothermic. With no further source of energy to support itself, the core of the star collapses on itself while the outer regions are blown off in a Type II supernova.[11]

Nickel-56 is unstable with respect to beta decay, and the final stable product of silicon burning is 56
26Fe
.

56
28Ni
 		→ 56
27Co
 		+ β+  t1/2 = 6.075(10) d
56
27Co
 		→ 56
26Fe
 		+ β+  t1/2 = 77.233(27) d
 Nuclide mass[12]Mass defect[13]Binding energy
per nucleon[14]
62
28Ni
61.9283451(6) u0.5700031(6) u8.563872(10) MeV
58
26Fe
57.9332756(8) u0.5331899(8) u8.563158(12) MeV
56
26Fe
55.9349375(7) u0.5141981(7) u8.553080(12) MeV

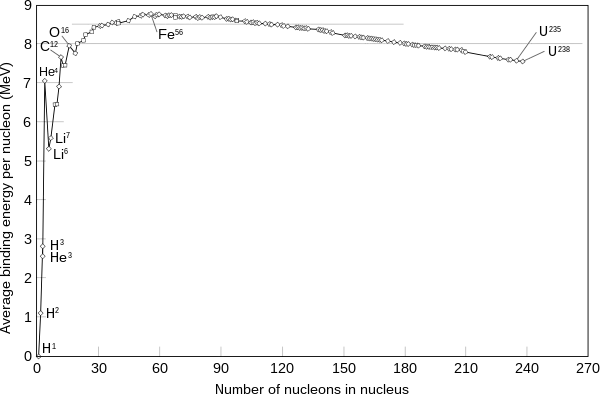
It is often incorrectly stated that iron-56 is exceptionally common because it is the most stable of all the nuclides.[10] This is not quite true: 62
28Ni
 and 58
26Fe
 have slightly higher binding energies per nucleon – that is, they are slightly more stable as nuclides – as can be seen from the table on the right.[15] However, there are no rapid nucleosynthetic routes to these nuclides.

In fact, there are several stable nuclides of elements from chromium to nickel around the top of the stability curve, accounting for their relative abundance in the universe. The nuclides which are not on the direct alpha-process pathway are formed by the s-process, the capture of slow neutrons within the star.

The curve of binding energy per nucleon (calculated from the nuclear mass defect) against the number of nucleons in the nucleus. Iron-56 is labelled near the very top of the curve: it can be seen that the "peak" is quite flat, which explains the existence of several common elements around iron.

See also

Notes and references

Notes

  1. ↑ In lighter stars, with less gravitational pressure, the alpha process is much slower and effectively stops at this stage as titanium-44 is unstable with respect to beta decay (t1/2 = 60.0(11) years).

References

  1. 1 2 M. Green, ed. (2002): Organometallic Chemistry, volume 10, page 283. Royal Society of Chemistry; 430 pages, ISBN 9780854043330
  2. ↑ Bravo, E. (2013). "Insights into thermonuclear supernovae from the incomplete Si-burning process". Astronomy & Astrophysics. 550: A24. arXiv:1212.2410. Bibcode:2013A&A...550A..24B. doi:10.1051/0004-6361/201220309. S2CID 49331289.
  3. ↑ Sherwood Taylor, F. (1942), Inorganic and Theoretical Chemistry (6th ed.), London: Heinemann, pp. 151–54, 727–28.
  4. ↑ Strecker, A. (1859), Theorien und Experimente zur Bestimmung der Atomgewichte der Elemente, Braunschweig: Friedrich Vieweg.
  5. ↑ "Proceedings of Societies [Report on the Law of Octaves]", Chemical News, 13: 113, 1866.
  6. ↑ Mendelejeff, D. (1869), "On the Relationship of the Properties of the Elements to their Atomic Weights", Z. Chem., 12: 405–6.
  7. ↑ Mendeléeff, D. (1889), "The Periodic Law of the Chemical Elements", J. Chem. Soc., 55: 634–56, doi:10.1039/ct8895500634.
  8. 1 2 Vogel, Arthur I. (1954), A Textbook of Macro and Semimicro Qualitative Inorganic Analysis (4th ed.), London: Longman, pp. 260–78, ISBN 0-582-44367-9.
  9. ↑ Vogel, Arthur I. (1954), A Textbook of Macro and Semimicro Qualitative Inorganic Analysis (4th ed.), London: Longman, pp. 592–611, ISBN 0-582-44367-9.
  10. 1 2 Greenwood, Norman N.; Earnshaw, Alan (1984). Chemistry of the Elements. Oxford: Pergamon Press. pp. 13–16. ISBN 978-0-08-022057-4..
  11. 1 2 Woosley, Stan; Janka, Thomas (2005), "The Physics of Core-Collapse Supernovae", Nature Physics, 1 (3): 147–54, arXiv:astro-ph/0601261, Bibcode:2005NatPh...1..147W, CiteSeerX 10.1.1.336.2176, doi:10.1038/nphys172, S2CID 118974639.
  12. ↑ Wapstra, A.H.; Audi, G.; Thibault, C. (2003), The AME2003 Atomic Mass Evaluation (Online ed.), National Nuclear Data Center. Based on:
  13. ↑ Particle Data Group (2008), "Review of Particle Physics" (PDF), Phys. Lett. B, 667 (1–5): 1–6, Bibcode:2008PhLB..667....1A, doi:10.1016/j.physletb.2008.07.018, hdl:1854/LU-685594, S2CID 227119789, archived from the original (PDF) on 2020-09-07, retrieved 2019-12-13. Data tables.
  14. ↑ Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2008). "CODATA Recommended Values of the Fundamental Physical Constants: 2006" (PDF). Reviews of Modern Physics. 80 (2): 633–730. arXiv:0801.0028. Bibcode:2008RvMP...80..633M. doi:10.1103/RevModPhys.80.633. Archived from the original (PDF) on 2017-10-01. Direct link to value.
  15. ↑ Fewell, M. P. (1995), "The atomic nuclide with the highest mean binding energy", Am. J. Phys., 63 (7): 653–58, Bibcode:1995AmJPh..63..653F, doi:10.1119/1.17828.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.