In geometry, a uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive (transitive on its vertices, isogonal, i.e. there is an isometry mapping any vertex onto any other). It follows that all vertices are congruent, and the polyhedron has a high degree of reflectional and rotational symmetry.

Uniform polyhedra can be divided between convex forms with convex regular polygon faces and star forms. Star forms have either regular star polygon faces or vertex figures or both.

This list includes these:

• all 75 nonprismatic uniform polyhedra;
• a few representatives of the infinite sets of prisms and antiprisms;
• one degenerate polyhedron, Skilling's figure with overlapping edges.

It was proven in Sopov (1970) that there are only 75 uniform polyhedra other than the infinite families of prisms and antiprisms. John Skilling discovered an overlooked degenerate example, by relaxing the condition that only two faces may meet at an edge. This is a degenerate uniform polyhedron rather than a uniform polyhedron, because some pairs of edges coincide.

Not included are:

• The uniform polyhedron compounds.
• 40 potential uniform polyhedra with degenerate vertex figures which have overlapping edges (not counted by Coxeter);
• The uniform tilings (infinite polyhedra)
  • 11 Euclidean convex uniform tilings;
  • 28 Euclidean nonconvex or apeirogonal uniform tilings;
  • Infinite number of uniform tilings in hyperbolic plane.
• Any polygons or 4-polytopes

Indexing

Four numbering schemes for the uniform polyhedra are in common use, distinguished by letters:

• [C] Coxeter et al., 1954, showed the convex forms as figures 15 through 32; three prismatic forms, figures 33–35; and the nonconvex forms, figures 36–92.
• [W] Wenninger, 1974, has 119 figures: 1–5 for the Platonic solids, 6–18 for the Archimedean solids, 19–66 for stellated forms including the 4 regular nonconvex polyhedra, and ended with 67–119 for the nonconvex uniform polyhedra.
• [K] Kaleido, 1993: The 80 figures were grouped by symmetry: 1–5 as representatives of the infinite families of prismatic forms with dihedral symmetry, 6–9 with tetrahedral symmetry, 10–26 with octahedral symmetry, 27–80 with icosahedral symmetry.
• [U] Mathematica, 1993, follows the Kaleido series with the 5 prismatic forms moved to last, so that the nonprismatic forms become 1–75.

Names of polyhedra by number of sides

There are generic geometric names for the most common polyhedra. The 5 Platonic solids are called a tetrahedron, hexahedron, octahedron, dodecahedron and icosahedron with 4, 6, 8, 12, and 20 sides respectively. The regular hexahedron is a cube.

Table of polyhedra

The convex forms are listed in order of degree of vertex configurations from 3 faces/vertex and up, and in increasing sides per face. This ordering allows topological similarities to be shown.

There are infinitely many prisms and antiprisms, one for each regular polygon; the ones up to the 12-gonal cases are listed.

Convex uniform polyhedra

Name	Picture	Vertex type	Wythoff symbol	Sym.	C#	W#	U#	K#	Vert.	Edges	Faces	Faces by type
Tetrahedron		3.3.3	3 | 2 3	Td	C15	W001	U01	K06	4	6	4	4{3}
Triangular prism		3.4.4	2 3 | 2	D3h	C33a	—	U76a	K01a	6	9	5	2{3} +3{4}
Truncated tetrahedron		3.6.6	2 3 | 3	Td	C16	W006	U02	K07	12	18	8	4{3} +4{6}
Truncated cube		3.8.8	2 3 | 4	Oh	C21	W008	U09	K14	24	36	14	8{3} +6{8}
Truncated dodecahedron		3.10.10	2 3 | 5	Ih	C29	W010	U26	K31	60	90	32	20{3} +12{10}
Cube		4.4.4	3 | 2 4	Oh	C18	W003	U06	K11	8	12	6	6{4}
Pentagonal prism		4.4.5	2 5 | 2	D5h	C33b	—	U76b	K01b	10	15	7	5{4} +2{5}
Hexagonal prism		4.4.6	2 6 | 2	D6h	C33c	—	U76c	K01c	12	18	8	6{4} +2{6}
Heptagonal prism		4.4.7	2 7 | 2	D7h	C33d	—	U76d	K01d	14	21	9	7{4} +2{7}
Octagonal prism		4.4.8	2 8 | 2	D8h	C33e	—	U76e	K01e	16	24	10	8{4} +2{8}
Enneagonal prism		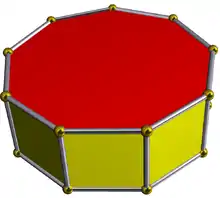4.4.9	2 9 | 2	D9h	C33f	—	U76f	K01f	18	27	11	9{4} +2{9}
Decagonal prism		4.4.10	2 10 | 2	D10h	C33g	—	U76g	K01g	20	30	12	10{4} +2{10}
Hendecagonal prism		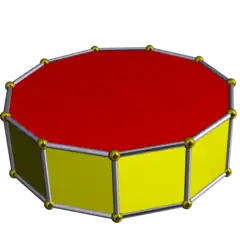4.4.11	2 11 | 2	D11h	C33h	—	U76h	K01h	22	33	13	11{4} +2{11}
Dodecagonal prism		4.4.12	2 12 | 2	D12h	C33i	—	U76i	K01i	24	36	14	12{4} +2{12}
Truncated octahedron		4.6.6	2 4 | 3	Oh	C20	W007	U08	K13	24	36	14	6{4} +8{6}
Truncated cuboctahedron		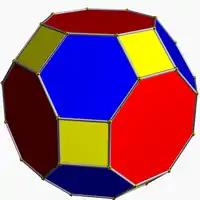4.6.8	2 3 4 |	Oh	C23	W015	U11	K16	48	72	26	12{4} +8{6} +6{8}
Truncated icosidodecahedron		4.6.10	2 3 5 |	Ih	C31	W016	U28	K33	120	180	62	30{4} +20{6} +12{10}
Dodecahedron		5.5.5	3 | 2 5	Ih	C26	W005	U23	K28	20	30	12	12{5}
Truncated icosahedron		5.6.6	2 5 | 3	Ih	C27	W009	U25	K30	60	90	32	12{5} +20{6}
Octahedron		3.3.3.3	4 | 2 3	Oh	C17	W002	U05	K10	6	12	8	8{3}
Square antiprism		3.3.3.4	| 2 2 4	D4d	C34a	—	U77a	K02a	8	16	10	8{3} +2{4}
Pentagonal antiprism		3.3.3.5	| 2 2 5	D5d	C34b	—	U77b	K02b	10	20	12	10{3} +2{5}
Hexagonal antiprism		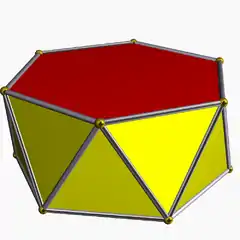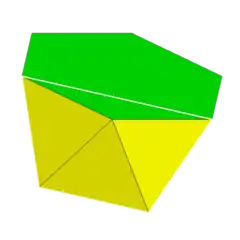3.3.3.6	| 2 2 6	D6d	C34c	—	U77c	K02c	12	24	14	12{3} +2{6}
Heptagonal antiprism		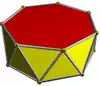3.3.3.7	| 2 2 7	D7d	C34d	—	U77d	K02d	14	28	16	14{3} +2{7}
Octagonal antiprism		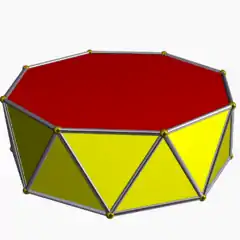3.3.3.8	| 2 2 8	D8d	C34e	—	U77e	K02e	16	32	18	16{3} +2{8}
Enneagonal antiprism		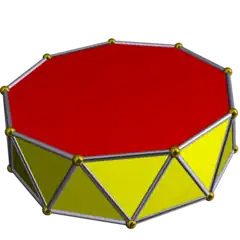3.3.3.9	| 2 2 9	D9d	C34f	—	U77f	K02f	18	36	20	18{3} +2{9}
Decagonal antiprism		3.3.3.10	| 2 2 10	D10d	C34g	—	U77g	K02g	20	40	22	20{3} +2{10}
Hendecagonal antiprism		3.3.3.11	| 2 2 11	D11d	C34h	—	U77h	K02h	22	44	24	22{3} +2{11}
Dodecagonal antiprism		3.3.3.12	| 2 2 12	D12d	C34i	—	U77i	K02i	24	48	26	24{3} +2{12}
Cuboctahedron		3.4.3.4	2 | 3 4	Oh	C19	W011	U07	K12	12	24	14	8{3} +6{4}
Rhombicuboctahedron		3.4.4.4	3 4 | 2	Oh	C22	W013	U10	K15	24	48	26	8{3} +(6+12){4}
Rhombicosidodecahedron		3.4.5.4	3 5 | 2	Ih	C30	W014	U27	K32	60	120	62	20{3} +30{4} +12{5}
Icosidodecahedron		3.5.3.5	2 | 3 5	Ih	C28	W012	U24	K29	30	60	32	20{3} +12{5}
Icosahedron		3.3.3.3.3	5 | 2 3	Ih	C25	W004	U22	K27	12	30	20	20{3}
Snub cube		3.3.3.3.4	| 2 3 4	O	C24	W017	U12	K17	24	60	38	(8+24){3} +6{4}
Snub dodecahedron		3.3.3.3.5	| 2 3 5	I	C32	W018	U29	K34	60	150	92	(20+60){3} +12{5}

Uniform star polyhedra

The forms containing only convex faces are listed first, followed by the forms with star faces. Again infinitely many prisms and antiprisms exist; they are listed here up to the 8-sided ones.

The uniform polyhedra | 5/2 3 3, | 5/2 3/2 3/2, | 5/3 5/2 3, | 3/2 5/3 3 5/2, and | (3/2) 5/3 (3) 5/2 have some faces occurring as coplanar pairs. (Coxeter et al. 1954, pp. 423, 425, 426; Skilling 1975, p. 123)

Name	Image	Wyth sym	Vert. fig	Sym.	C#	W#	U#	K#	Vert.	Edges	Faces	Chi	Orient- able?	Dens.	Faces by type
Octahemioctahedron		3/2 3 | 3	6.3/2.6.3	Oh	C37	W068	U03	K08	12	24	12	0	Yes		8{3}+4{6}
Tetrahemihexahedron		3/2 3 | 2	4.3/2.4.3	Td	C36	W067	U04	K09	6	12	7	1	No		4{3}+3{4}
Cubohemioctahedron		4/3 4 | 3	6.4/3.6.4	Oh	C51	W078	U15	K20	12	24	10	−2	No		6{4}+4{6}
Great dodecahedron		5/2 | 2 5	(5.5.5.5.5)/2	Ih	C44	W021	U35	K40	12	30	12	−6	Yes	3	12{5}
Great icosahedron		5/2 | 2 3	(3.3.3.3.3)/2	Ih	C69	W041	U53	K58	12	30	20	2	Yes	7	20{3}
Great ditrigonal icosidodecahedron		3/2 | 3 5	(5.3.5.3.5.3)/2	Ih	C61	W087	U47	K52	20	60	32	−8	Yes	6	20{3}+12{5}
Small rhombihexahedron		2 4 (3/2 4/2) |	4.8.4/3.8/7	Oh	C60	W086	U18	K23	24	48	18	−6	No		12{4}+6{8}
Small cubicuboctahedron		3/2 4 | 4	8.3/2.8.4	Oh	C38	W069	U13	K18	24	48	20	−4	Yes	2	8{3}+6{4}+6{8}
Great rhombicuboctahedron		3/2 4 | 2	4.3/2.4.4	Oh	C59	W085	U17	K22	24	48	26	2	Yes	5	8{3}+(6+12){4}
Small dodecahemi- dodecahedron		5/4 5 | 5	10.5/4.10.5	Ih	C65	W091	U51	K56	30	60	18	−12	No		12{5}+6{10}
Great dodecahem- icosahedron		5/4 5 | 3	6.5/4.6.5	Ih	C81	W102	U65	K70	30	60	22	−8	No		12{5}+10{6}
Small icosihemi- dodecahedron		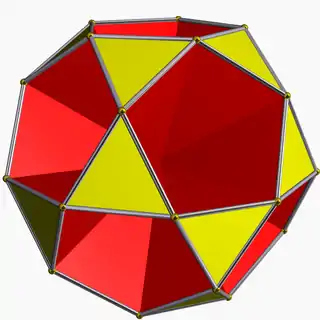3/2 3 | 5	10.3/2.10.3	Ih	C63	W089	U49	K54	30	60	26	−4	No		20{3}+6{10}
Small dodecicosahedron		3 5 (3/2 5/4) |	10.6.10/9.6/5	Ih	C64	W090	U50	K55	60	120	32	−28	No		20{6}+12{10}
Small rhombidodecahedron		2 5 (3/2 5/2) |	10.4.10/9.4/3	Ih	C46	W074	U39	K44	60	120	42	−18	No		30{4}+12{10}
Small dodecicosi- dodecahedron		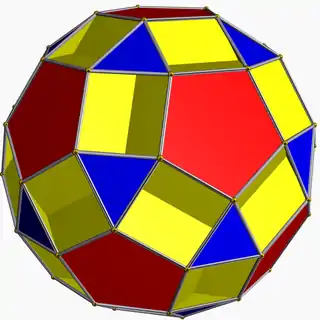3/2 5 | 5	10.3/2.10.5	Ih	C42	W072	U33	K38	60	120	44	−16	Yes	2	20{3}+12{5}+12{10}
Rhombicosahedron		2 3 (5/4 5/2) |	6.4.6/5.4/3	Ih	C72	W096	U56	K61	60	120	50	−10	No		30{4}+20{6}
Great icosicosi- dodecahedron		3/2 5 | 3	6.3/2.6.5	Ih	C62	W088	U48	K53	60	120	52	−8	Yes	6	20{3}+12{5}+20{6}
Pentagrammic prism		2 5/2 | 2	5/2.4.4	D5h	C33b	—	U78a	K03a	10	15	7	2	Yes	2	5{4}+2{5/2}
Heptagrammic prism (7/2)		2 7/2 | 2	7/2.4.4	D7h	C33d	—	U78b	K03b	14	21	9	2	Yes	2	7{4}+2{7/2}
Heptagrammic prism (7/3)		2 7/3 | 2	7/3.4.4	D7h	C33d	—	U78c	K03c	14	21	9	2	Yes	3	7{4}+2{7/3}
Octagrammic prism		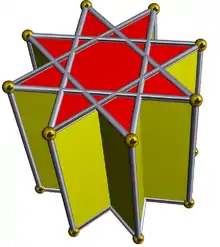2 8/3 | 2	8/3.4.4	D8h	C33e	—	U78d	K03d	16	24	10	2	Yes	3	8{4}+2{8/3}
Pentagrammic antiprism		| 2 2 5/2	5/2.3.3.3	D5h	C34b	—	U79a	K04a	10	20	12	2	Yes	2	10{3}+2{5/2}
Pentagrammic crossed-antiprism		| 2 2 5/3	5/3.3.3.3	D5d	C35a	—	U80a	K05a	10	20	12	2	Yes	3	10{3}+2{5/2}
Heptagrammic antiprism (7/2)		| 2 2 7/2	7/2.3.3.3	D7h	C34d	—	U79b	K04b	14	28	16	2	Yes	3	14{3}+2{7/2}
Heptagrammic antiprism (7/3)		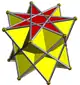| 2 2 7/3	7/3.3.3.3	D7d	C34d	—	U79c	K04c	14	28	16	2	Yes	3	14{3}+2{7/3}
Heptagrammic crossed-antiprism		| 2 2 7/4	7/4.3.3.3	D7h	C35b	—	U80b	K05b	14	28	16	2	Yes	4	14{3}+2{7/3}
Octagrammic antiprism		| 2 2 8/3	8/3.3.3.3	D8d	C34e	—	U79d	K04d	16	32	18	2	Yes	3	16{3}+2{8/3}
Octagrammic crossed-antiprism		| 2 2 8/5	8/5.3.3.3	D8d	C35c	—	U80c	K05c	16	32	18	2	Yes	5	16{3}+2{8/3}
Small stellated dodecahedron		5 | 2 5/2	(5/2)5	Ih	C43	W020	U34	K39	12	30	12	−6	Yes	3	12{5/2}
Great stellated dodecahedron		3 | 2 5/2	(5/2)3	Ih	C68	W022	U52	K57	20	30	12	2	Yes	7	12{5/2}
Ditrigonal dodeca- dodecahedron		3 | 5/3 5	(5/3.5)3	Ih	C53	W080	U41	K46	20	60	24	−16	Yes	4	12{5}+12{5/2}
Small ditrigonal icosidodecahedron		3 | 5/2 3	(5/2.3)3	Ih	C39	W070	U30	K35	20	60	32	−8	Yes	2	20{3}+12{5/2}
Stellated truncated hexahedron		2 3 | 4/3	8/3.8/3.3	Oh	C66	W092	U19	K24	24	36	14	2	Yes	7	8{3}+6{8/3}
Great rhombihexahedron		2 4/3 (3/2 4/2) |	4.8/3.4/3.8/5	Oh	C82	W103	U21	K26	24	48	18	−6	No		12{4}+6{8/3}
Great cubicuboctahedron		3 4 | 4/3	8/3.3.8/3.4	Oh	C50	W077	U14	K19	24	48	20	−4	Yes	4	8{3}+6{4}+6{8/3}
Great dodecahemi- dodecahedron		5/3 5/2 | 5/3	10/3.5/3.10/3.5/2	Ih	C86	W107	U70	K75	30	60	18	−12	No		12{5/2}+6{10/3}
Small dodecahemi- cosahedron		5/3 5/2 | 3	6.5/3.6.5/2	Ih	C78	W100	U62	K67	30	60	22	−8	No		12{5/2}+10{6}
Dodeca- dodecahedron		2 | 5 5/2	(5/2.5)2	Ih	C45	W073	U36	K41	30	60	24	−6	Yes	3	12{5}+12{5/2}
Great icosihemi- dodecahedron		3/2 3 | 5/3	10/3.3/2.10/3.3	Ih	C85	W106	U71	K76	30	60	26	−4	No		20{3}+6{10/3}
Great icosidodecahedron		2 | 3 5/2	(5/2.3)2	Ih	C70	W094	U54	K59	30	60	32	2	Yes	7	20{3}+12{5/2}
Cubitruncated cuboctahedron		4/3 3 4 |	8/3.6.8	Oh	C52	W079	U16	K21	48	72	20	−4	Yes	4	8{6}+6{8}+6{8/3}
Great truncated cuboctahedron		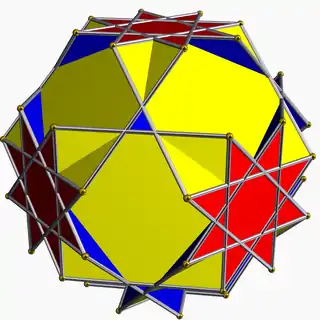4/3 2 3 |	8/3.4.6/5	Oh	C67	W093	U20	K25	48	72	26	2	Yes	1	12{4}+8{6}+6{8/3}
Truncated great dodecahedron		2 5/2 | 5	10.10.5/2	Ih	C47	W075	U37	K42	60	90	24	−6	Yes	3	12{5/2}+12{10}
Small stellated truncated dodecahedron		2 5 | 5/3	10/3.10/3.5	Ih	C74	W097	U58	K63	60	90	24	−6	Yes	9	12{5}+12{10/3}
Great stellated truncated dodecahedron		2 3 | 5/3	10/3.10/3.3	Ih	C83	W104	U66	K71	60	90	32	2	Yes	13	20{3}+12{10/3}
Truncated great icosahedron		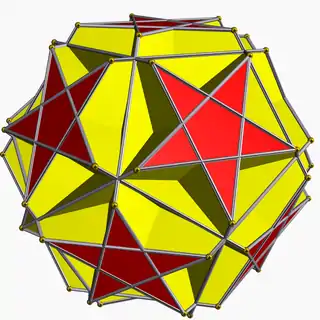2 5/2 | 3	6.6.5/2	Ih	C71	W095	U55	K60	60	90	32	2	Yes	7	12{5/2}+20{6}
Great dodecicosahedron		3 5/3(3/2 5/2) |	6.10/3.6/5.10/7	Ih	C79	W101	U63	K68	60	120	32	−28	No		20{6}+12{10/3}
Great rhombidodecahedron		2 5/3 (3/2 5/4) |	4.10/3.4/3.10/7	Ih	C89	W109	U73	K78	60	120	42	−18	No		30{4}+12{10/3}
Icosidodeca- dodecahedron		5/3 5 | 3	6.5/3.6.5	Ih	C56	W083	U44	K49	60	120	44	−16	Yes	4	12{5}+12{5/2}+20{6}
Small ditrigonal dodecicosi- dodecahedron		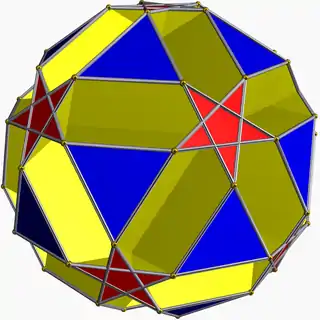5/3 3 | 5	10.5/3.10.3	Ih	C55	W082	U43	K48	60	120	44	−16	Yes	4	20{3}+12{5/2}+12{10}
Great ditrigonal dodecicosi- dodecahedron		3 5 | 5/3	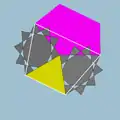10/3.3.10/3.5	Ih	C54	W081	U42	K47	60	120	44	−16	Yes	4	20{3}+12{5}+12{10/3}
Great dodecicosi- dodecahedron		5/2 3 | 5/3	10/3.5/2.10/3.3	Ih	C77	W099	U61	K66	60	120	44	−16	Yes	10	20{3}+12{5/2}+12{10/3}
Small icosicosi- dodecahedron		5/2 3 | 3	6.5/2.6.3	Ih	C40	W071	U31	K36	60	120	52	−8	Yes	2	20{3}+12{5/2}+20{6}
Rhombidodeca- dodecahedron		5/2 5 | 2	4.5/2.4.5	Ih	C48	W076	U38	K43	60	120	54	−6	Yes	3	30{4}+12{5}+12{5/2}
Great rhombicosi- dodecahedron		5/3 3 | 2	4.5/3.4.3	Ih	C84	W105	U67	K72	60	120	62	2	Yes	13	20{3}+30{4}+12{5/2}
Icositruncated dodeca- dodecahedron		3 5 5/3 |	10/3.6.10	Ih	C57	W084	U45	K50	120	180	44	−16	Yes	4	20{6}+12{10}+12{10/3}
Truncated dodeca- dodecahedron		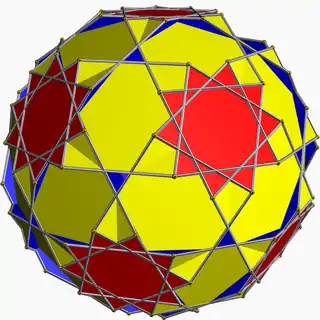2 5 5/3 |	10/3.4.10/9	Ih	C75	W098	U59	K64	120	180	54	−6	Yes	3	30{4}+12{10}+12{10/3}
Great truncated icosidodecahedron		2 3 5/3 |	10/3.4.6	Ih	C87	W108	U68	K73	120	180	62	2	Yes	13	30{4}+20{6}+12{10/3}
Snub dodeca- dodecahedron		| 2 5/2 5	3.3.5/2.3.5	I	C49	W111	U40	K45	60	150	84	−6	Yes	3	60{3}+12{5}+12{5/2}
Inverted snub dodeca- dodecahedron		| 5/3 2 5	3.5/3.3.3.5	I	C76	W114	U60	K65	60	150	84	−6	Yes	9	60{3}+12{5}+12{5/2}
Great snub icosidodecahedron		| 2 5/2 3	34.5/2	I	C73	W113	U57	K62	60	150	92	2	Yes	7	(20+60){3}+12{5/2}
Great inverted snub icosidodecahedron		| 5/3 2 3	34.5/3	I	C88	W116	U69	K74	60	150	92	2	Yes	13	(20+60){3}+12{5/2}
Great retrosnub icosidodecahedron		| 2 3/2 5/3	(34.5/2)/2	I	C90	W117	U74	K79	60	150	92	2	Yes	37	(20+60){3}+12{5/2}
Great snub dodecicosi- dodecahedron		| 5/3 5/2 3	33.5/3.3.5/2	I	C80	W115	U64	K69	60	180	104	−16	Yes	10	(20+60){3}+(12+12){5/2}
Snub icosidodeca- dodecahedron		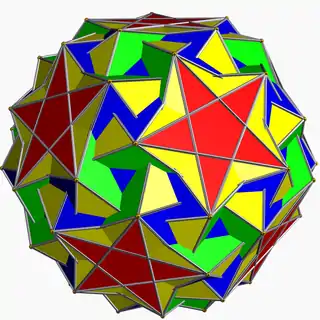| 5/3 3 5	33.5.3.5/3	I	C58	W112	U46	K51	60	180	104	−16	Yes	4	(20+60){3}+12{5}+12{5/2}
Small snub icos- icosidodecahedron		| 5/2 3 3	35.5/2	Ih	C41	W110	U32	K37	60	180	112	−8	Yes	2	(40+60){3}+12{5/2}
Small retrosnub icosicosi- dodecahedron		| 3/2 3/2 5/2	(35.5/2)/2	Ih	C91	W118	U72	K77	60	180	112	−8	Yes	38	(40+60){3}+12{5/2}
Great dirhombicosi- dodecahedron		| 3/2 5/3 3 5/2	(4.5/3.4.3. 4.5/2.4.3/2)/2	Ih	C92	W119	U75	K80	60	240	124	−56	No		40{3}+60{4}+24{5/2}

Special case

Name	Image	Wyth sym	Vert. fig	Sym.	C#	W#	U#	K#	Vert.	Edges	Faces	Chi	Orient- able?	Dens.	Faces by type
Great disnub dirhombidodecahedron		| (3/2) 5/3 (3) 5/2	(5/2.4.3.3.3.4. 5/3. 4.3/2.3/2.3/2.4)/2	Ih	—	—	—	—	60	360 (*)	204	−96	No		120{3}+60{4}+24{5/2}

The great disnub dirhombidodecahedron has 240 of its 360 edges coinciding in space in 120 pairs. Because of this edge-degeneracy, it is not always considered to be a uniform polyhedron.

Column key

• Uniform indexing: U01–U80 (Tetrahedron first, Prisms at 76+)
• Kaleido software indexing: K01–K80 (K_n = U_n–5 for n = 6 to 80) (prisms 1–5, Tetrahedron etc. 6+)
• Magnus Wenninger Polyhedron Models: W001-W119
  • 1–18: 5 convex regular and 13 convex semiregular
  • 20–22, 41: 4 non-convex regular
  • 19–66: Special 48 stellations/compounds (Nonregulars not given on this list)
  • 67–109: 43 non-convex non-snub uniform
  • 110–119: 10 non-convex snub uniform
• Chi: the Euler characteristic, χ. Uniform tilings on the plane correspond to a torus topology, with Euler characteristic of zero.
• Density: the Density (polytope) represents the number of windings of a polyhedron around its center. This is left blank for non-orientable polyhedra and hemipolyhedra (polyhedra with faces passing through their centers), for which the density is not well-defined.
• Note on Vertex figure images:
  • The white polygon lines represent the "vertex figure" polygon. The colored faces are included on the vertex figure images help see their relations. Some of the intersecting faces are drawn visually incorrectly because they are not properly intersected visually to show which portions are in front.

See also

• List of uniform polyhedra by vertex figure
• List of uniform polyhedra by Wythoff symbol
• List of uniform polyhedra by Schwarz triangle

References

• Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954). "Uniform polyhedra". Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. The Royal Society. 246 (916): 401–450. Bibcode:1954RSPTA.246..401C. doi:10.1098/rsta.1954.0003. ISSN 0080-4614. JSTOR 91532. MR 0062446. S2CID 202575183.
• Skilling, J. (1975). "The complete set of uniform polyhedra". Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. 278 (1278): 111–135. Bibcode:1975RSPTA.278..111S. doi:10.1098/rsta.1975.0022. ISSN 0080-4614. JSTOR 74475. MR 0365333. S2CID 122634260.
• Sopov, S. P. (1970). "A proof of the completeness on the list of elementary homogeneous polyhedra". Ukrainskiui Geometricheskiui Sbornik (8): 139–156. MR 0326550.
• Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
• Wenninger, Magnus (1983). Dual Models. Cambridge University Press. ISBN 0-521-54325-8.

External links

• Stella: Polyhedron Navigator – Software able to generate and print nets for all uniform polyhedra. Used to create most images on this page.
• Paper models
• Uniform indexing: U1-U80, (Tetrahedron first)
  • Uniform Polyhedra (80), Paul Bourke
  • Weisstein, Eric W. "Uniform Polyhedron". MathWorld.
  • http://www.mathconsult.ch/showroom/unipoly
    • All uniform polyhedra by rotation group
  • https://web.archive.org/web/20171110075259/http://gratrix.net/polyhedra/uniform/summary/
  • http://www.it-c.dk/edu/documentation/mathworks/math/math/u/u034.htm
  • http://www.buddenbooks.com/jb/uniform/
• Kaleido Indexing: K1-K80 (Pentagonal prism first)
  • https://www.math.technion.ac.il/~rl/kaleido
    • https://web.archive.org/web/20110927223146/http://www.math.technion.ac.il/~rl/docs/uniform.pdf Uniform Solution for Uniform Polyhedra
  • http://bulatov.org/polyhedra/uniform
  • http://www.orchidpalms.com/polyhedra/uniform/uniform.html
• Also
  • http://www.polyedergarten.de/polyhedrix/e_klintro.htm