Illustration of Riemann's 'dualist' system: minor as upside down major.

Starting from the symmetrical chords, otonal chords flatten one note, while utonal chords sharpen one note, as observed by Richard Cohn.

Neo-Riemannian theory is a loose collection of ideas present in the writings of music theorists such as David Lewin, Brian Hyer, Richard Cohn, and Henry Klumpenhouwer. What binds these ideas is a central commitment to relating harmonies directly to each other, without necessary reference to a tonic. Initially, those harmonies were major and minor triads; subsequently, neo-Riemannian theory was extended to standard dissonant sonorities as well. Harmonic proximity is characteristically gauged by efficiency of voice leading. Thus, C major and E minor triads are close by virtue of requiring only a single semitonal shift to move from one to the other. Motion between proximate harmonies is described by simple transformations. For example, motion between a C major and E minor triad, in either direction, is executed by an "L" transformation. Extended progressions of harmonies are characteristically displayed on a geometric plane, or map, which portrays the entire system of harmonic relations. Where consensus is lacking is on the question of what is most central to the theory: smooth voice leading, transformations, or the system of relations that is mapped by the geometries. The theory is often invoked when analyzing harmonic practices within the Late Romantic period characterized by a high degree of chromaticism, including work of Schubert, Liszt, Wagner and Bruckner.^[1]

Neo-Riemannian theory is named after Hugo Riemann (1849–1919), whose "dualist" system for relating triads was adapted from earlier 19th-century harmonic theorists. (The term "dualism" refers to the emphasis on the inversional relationship between major and minor, with minor triads being considered "upside down" versions of major triads; this "dualism" is what produces the change-in-direction described above. See also: Utonality) In the 1880s, Riemann proposed a system of transformations that related triads directly to each other ^[2] The revival of this aspect of Riemann's writings, independently of the dualist premises under which they were initially conceived, originated with David Lewin (1933–2003), particularly in his article "Amfortas's Prayer to Titurel and the Role of D in Parsifal" (1984) and his influential book, Generalized Musical Intervals and Transformations (1987). Subsequent development in the 1990s and 2000s has expanded the scope of neo-Riemannian theory considerably, with further mathematical systematization to its basic tenets, as well as inroads into 20th century repertoires and music psychology.^[1]

Triadic transformations and voice leading

The principal transformations of neo-Riemannian triadic theory connect triads of different species (major and minor), and are their own inverses (a second application undoes the first). These transformations are purely harmonic, and do not need any particular voice leading between chords: all instances of motion from a C major to a C minor triad represent the same neo-Riemannian transformation, no matter how the voices are distributed in register.

Neo-Riemannian music theory's PLR operations applied to a minor chord Q.

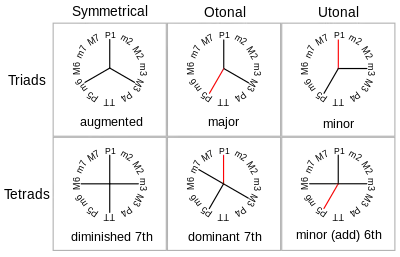
The three transformations move one of the three notes of the triad to produce a different triad:

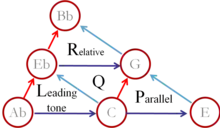
• The P transformation exchanges a triad for its Parallel. In a Major Triad move the third down a semitone (C major to C minor), in a Minor Triad move the third up a semitone (C minor to C major)
• The R transformation exchanges a triad for its Relative. In a Major Triad move the fifth up a tone (C major to A minor), in a Minor Triad move the root down a tone (A minor to C major)
• The L transformation exchanges a triad for its Leading-Tone Exchange. In a Major Triad the root moves down by a semitone (C major to E minor), in a Minor Triad the fifth moves up by a semitone (E minor to C major)

Observe that P preserves the perfect fifth interval (so given say C and G there are only two candidates for the third note: E and E♭), L preserves the minor third interval (given E and G our candidates are C and B) and R preserves the major third interval (given C and E our candidates are G and A).

Secondary operations can be constructed by combining these basic operations:

• The N (or Nebenverwandt) relation exchanges a major triad for its minor subdominant, and a minor triad for its major dominant (C major and F minor). The "N" transformation can be obtained by applying R, L, and P successively.^[3]
• The S (or Slide) relation exchanges two triads that share a third (C major and C♯ minor); it can be obtained by applying L, P, and R successively in that order.^[4]
• The H relation (LPL) exchanges a triad for its hexatonic pole (C major and A♭ minor)^[5]

Any combination of the L, P, and R transformations will act inversely on major and minor triads: for instance, R-then-P transposes C major down a minor third, to A major via A minor, whilst transposing C minor to E♭ minor up a minor 3rd via E♭ major.

Initial work in neo-Riemannian theory treated these transformations in a largely harmonic manner, without explicit attention to voice leading. Later, Cohn pointed out that neo-Riemannian concepts arise naturally when thinking about certain problems in voice leading.^[6][7] For example, two triads (major or minor) share two common tones and can be connected by stepwise voice leading the third voice if and only if they are linked by one of the L, P, R transformations described above.^[6] (This property of stepwise voice leading in a single voice is called voice-leading parsimony.) Note that here the emphasis on inversional relationships arises naturally, as a byproduct of interest in "parsimonious" voice leading, rather than being a fundamental theoretical postulate, as it was in Riemann's work.

More recently, Dmitri Tymoczko has argued that the connection between neo-Riemannian operations and voice leading is only approximate (see below).^[8] Furthermore, the formalism of neo-Riemannian theory treats voice leading in a somewhat oblique manner: "neo-Riemannian transformations," as defined above, are purely harmonic relationships that do not necessarily involve any particular mapping between the chords' notes.^[7]

Graphical representations

Pitches in the Tonnetz are connected by lines if they are separated by minor third, major third, or perfect fifth. Interpreted as a torus, the Tonnetz has 12 nodes (pitches) and 24 triangles (triads).

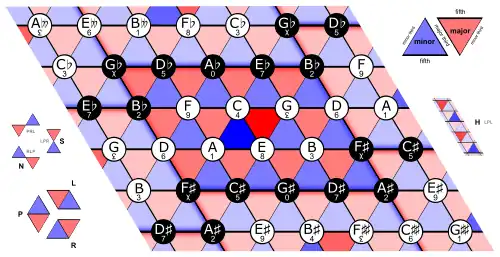
Neo-Riemannian transformations can be modeled with several interrelated geometric structures. The Riemannian Tonnetz ("tonal grid," shown on the right) is a planar array of pitches along three simplicial axes, corresponding to the three consonant intervals. Major and minor triads are represented by triangles which tile the plane of the Tonnetz. Edge-adjacent triads share two common pitches, and so the principal transformations are expressed as minimal motion of the Tonnetz. Unlike the historical theorist for which it is named, neo-Riemannian theory typically assumes enharmonic equivalence (G♯ = A♭), which wraps the planar graph into a torus.

David Bulger's toroidal view of the neo-Riemannian Tonnetz.

Alternate tonal geometries have been described in neo-Riemannian theory that isolate or expand upon certain features of the classical Tonnetz. Richard Cohn developed the Hyper Hexatonic system to describe motion within and between separate major third cycles, all of which exhibit what he formulates as "maximal smoothness." (Cohn, 1996).^[6] Another geometric figure, Cube Dance, was invented by Jack Douthett; it features the geometric dual of the Tonnetz, where triads are vertices instead of triangles (Douthett and Steinbach, 1998) and are interspersed with augmented triads, allowing smoother voice-leadings.

Many of the geometrical representations associated with neo-Riemannian theory are unified into a more general framework by the continuous voice-leading spaces explored by Clifton Callender, Ian Quinn, and Dmitri Tymoczko. This work originates in 2004, when Callender described a continuous space in which points represented three-note "chord types" (such as "major triad"), using the space to model "continuous transformations" in which voices slid continuously from one note to another.^[9] Later, Tymoczko showed that paths in Callender's space were isomorphic to certain classes of voice leadings (the "individually T related" voice leadings discussed in Tymoczko 2008) and developed a family of spaces more closely analogous to those of neo-Riemannian theory. In Tymoczko's spaces, points represent particular chords of any size (such as "C major") rather than more general chord types (such as "major triad").^[7][10] Finally, Callender, Quinn, and Tymoczko together proposed a unified framework connecting these and many other geometrical spaces representing diverse range of music-theoretical properties.^[11]

The Harmonic table note layout is a modern day realisation of this graphical representation to create a musical interface.

Planet-4D model embeds the traditional Tonnetz onto the surface of a Hypersphere

In 2011, Gilles Baroin presented the Planet-4D model,^[12] a new visualisation system based on graph theory that embeds the traditional Tonnetz on a 4D Hypersphere. Another recent continuous version of the Tonnetz — simultaneously in original and dual form — is the Torus of phases^[13] which enables even finer analyses, for instance in early romantic music.^[14]

Criticism

Neo-Riemannian theorists often analyze chord progressions as combinations of the three basic LPR transformations, the only ones that preserve two common tones. Thus the progression from C major to E major might be analyzed as L-then-P, which is a 2-unit motion since it involves two transformations. (This same transformation sends C minor to A♭ minor, since L of C minor is A♭ major, while P of A♭ major is A♭ minor.) These distances reflect voice-leading only imperfectly.^[8] For example, according to strains of neo-Riemannian theory that prioritize common-tone preservation, the C major triad is closer to F major than to F minor, since C major can be transformed into F major by R-then-L, while it takes three moves to get from C major to F minor (R-then-L-then-P). However, from a chromatic voice-leading perspective F minor is closer to C major than F major is, since it takes just two semitones of motion to transform F minor into C major (A♭->G and F->E) whereas it takes three semitones to transform F major into C major. Thus LPR transformations are unable to account for the voice-leading efficiency of the IV-iv-I progression, one of the basic routines of nineteenth-century harmony.^[8] Note that similar points can be made about common tones: on the Tonnetz, F minor and E♭ minor are both three steps from C major, even though F minor and C major have one common tone, while E♭ minor and C major have none.

Underlying these discrepancies are different ideas about whether harmonic proximity is maximized when two common tones are shared, or when the total voice-leading distance is minimized. For example, in the R transformation, a single voice moves by whole step; in the N or S transformation, two voices move by semitone. When common-tone maximization is prioritized, R is more efficient; when voice-leading efficiency is measured by summing the motions of the individual voices, the transformations are equivalently efficient. Early neo-Riemannian theory conflated these two conceptions. More recent work has disentangled them, and measures distance unilaterally by voice-leading proximity independently of common-tone preservation. Accordingly, the distinction between "primary" and "secondary" transformations becomes problematized. As early as 1992, Jack Douthett created an exact geometric model of inter-triadic voice-leading by interpolating augmented triads between R-related triads, which he called "Cube Dance".^[15] Though Douthett's figure was published in 1998, its superiority as a model of voice leading was not fully appreciated until much later, in the wake of the geometrical work of Callender, Quinn, and Tymoczko; indeed, the first detailed comparison of "Cube Dance" to the neo-Riemannian "Tonnetz" appeared in 2009, more than fifteen years after Douthett's initial discovery of his figure.^[8] In this line of research, the triadic transformations lose the foundational status that they held in the early phases of neo-Riemannian theory. The geometries to which voice-leading proximity give rise attain central status, and the transformations become heuristic labels for certain kinds of standard routines, rather than their defining property.

Extensions

Beyond its application to triadic chord progressions, neo-Riemannian theory has inspired numerous subsequent investigations. These include

• Voice-leading proximity among chords with more than three tones- among species of hexachords, such as the Mystic chord (Callender, 1998)^[16]
• Common-tone proximity among dissonant trichords ^[17]
• Progressions among triads within diatonic rather than chromatic space.
• Transformations among scales of various sizes and species (in the work of Dmitri Tymoczko).^[18]
• Transformations among all possible triads, not necessarily strict mode-shifting involutions (Hook, 2002).^[19]
• Transformations between chords of differing cardinality, called cross-type transformations (Hook, 2007).^[20]

Some of these extensions share neo-Riemannian theory's concern with non-traditional relations among familiar tonal chords; others apply voice-leading proximity or harmonic transformation to characteristically atonal chords.

See also

• Diatonic function
• Musical set theory
• Riemannian theory
• Transformational theory

References

External links

TouchTonnetz – an interactive mobile app to explore Neo-Riemannian Theory – Android or iPhone

Further reading

• Lewin, David. "Amfortas's Prayer to Titurel and the Role of D in 'Parsifal': The Tonal Spaces of the Drama and the Enharmonic Cb/B," 19th Century Music 7/3 (1984), 336–349.
• Lewin, David. Generalized Musical Intervals and Transformations (Yale University Press: New Haven, CT, 1987). ISBN 978-0-300-03493-6.
• Cohn, Richard. 'An Introduction to Neo-Riemannian Theory: A Survey and Historical Perspective", Journal of Music Theory, 42/2 (1998), 167–180.
• Lerdahl, Fred. Tonal Pitch Space (Oxford University Press: New York, 2001). ISBN 978-0-19-505834-5.
• Hook, Julian. Uniform Triadic Transformations (Ph.D. dissertation, Indiana University, 2002).
• Kopp, David. Chromatic Transformations in Nineteenth-century Music (Cambridge University Press, 2002). ISBN 978-0-521-80463-9.
• Hyer, Brian. "Reimag(in)ing Riemann", Journal of Music Theory, 39/1 (1995), 101–138.
• Mooney, Michael Kevin. The 'Table of Relations' and Music Psychology in Hugo Riemann's Chromatic Theory (Ph.D. dissertation, Columbia University, 1996).
• Cohn, Richard. "Neo-Riemannian Operations, Parsimonious Trichords, and their Tonnetz Representations", Journal of Music Theory, 41/1 (1997), 1–66.
• Cohn, Richard. Audacious Euphony: Chromaticism and the Triad's Second Nature (New York: Oxford University Press, 2012). ISBN 978-0-19-977269-8.
• Gollin, Edward and Alexander Rehding, Oxford Handbook of Neo-Riemannian Music Theories (New York: Oxford University Press, 2011). ISBN 978-0-19-532133-3.