 Involutional symmetry Cs, (*) [ ] = |
 Cyclic symmetry Cnv, (*nn) [n] = |
 Dihedral symmetry Dnh, (*n22) [n,2] = | |
| Polyhedral group, [n,3], (*n32) | |||
|---|---|---|---|
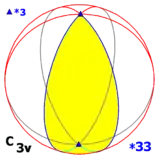
 Tetrahedral symmetry Td, (*332) [3,3] = |
 Octahedral symmetry Oh, (*432) [4,3] = |
 Icosahedral symmetry Ih, (*532) [5,3] = | |
In geometry, the polyhedral group is any of the symmetry groups of the Platonic solids.
Groups
There are three polyhedral groups:
- The tetrahedral group of order 12, rotational symmetry group of the regular tetrahedron. It is isomorphic to A4.
- The conjugacy classes of T are:
- identity
- 4 × rotation by 120°, order 3, cw
- 4 × rotation by 120°, order 3, ccw
- 3 × rotation by 180°, order 2
- The conjugacy classes of T are:
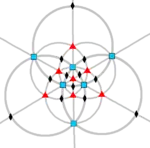
- The octahedral group of order 24, rotational symmetry group of the cube and the regular octahedron. It is isomorphic to S4.
- The conjugacy classes of O are:
- identity
- 6 × rotation by ±90° around vertices, order 4
- 8 × rotation by ±120° around triangle centers, order 3
- 3 × rotation by 180° around vertices, order 2
- 6 × rotation by 180° around midpoints of edges, order 2
- The conjugacy classes of O are:
- The icosahedral group of order 60, rotational symmetry group of the regular dodecahedron and the regular icosahedron. It is isomorphic to A5.
- The conjugacy classes of I are:
- identity
- 12 × rotation by ±72°, order 5
- 12 × rotation by ±144°, order 5
- 20 × rotation by ±120°, order 3
- 15 × rotation by 180°, order 2
- The conjugacy classes of I are:
These symmetries double to 24, 48, 120 respectively for the full reflectional groups. The reflection symmetries have 6, 9, and 15 mirrors respectively. The octahedral symmetry, [4,3] can be seen as the union of 6 tetrahedral symmetry [3,3] mirrors, and 3 mirrors of dihedral symmetry Dih2, [2,2]. Pyritohedral symmetry is another doubling of tetrahedral symmetry.
The conjugacy classes of full tetrahedral symmetry, Td≅S4, are:
- identity
- 8 × rotation by 120°
- 3 × rotation by 180°
- 6 × reflection in a plane through two rotation axes
- 6 × rotoreflection by 90°
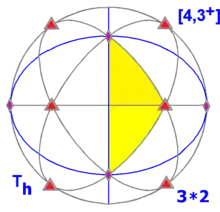
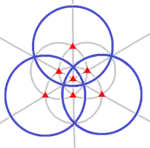
The conjugacy classes of pyritohedral symmetry, Th, include those of T, with the two classes of 4 combined, and each with inversion:
- identity
- 8 × rotation by 120°
- 3 × rotation by 180°
- inversion
- 8 × rotoreflection by 60°
- 3 × reflection in a plane
The conjugacy classes of the full octahedral group, Oh≅S4 × C2, are:
- inversion
- 6 × rotoreflection by 90°
- 8 × rotoreflection by 60°
- 3 × reflection in a plane perpendicular to a 4-fold axis
- 6 × reflection in a plane perpendicular to a 2-fold axis
The conjugacy classes of full icosahedral symmetry, Ih≅A5 × C2, include also each with inversion:
- inversion
- 12 × rotoreflection by 108°, order 10
- 12 × rotoreflection by 36°, order 10
- 20 × rotoreflection by 60°, order 6
- 15 × reflection, order 2
Chiral polyhedral groups
| Name (Orb.) |
Coxeter notation |
Order | Abstract structure |
Rotation points #valence |
Diagrams | |||
|---|---|---|---|---|---|---|---|---|
| Orthogonal | Stereographic | |||||||
| T (332) |
[3,3]+ | 12 | A4 | 43 32 | 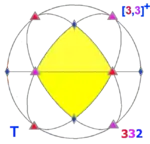 |
 |
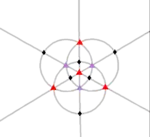 |
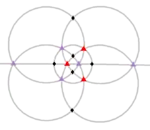 |
| Th (3*2) |
[4,3+] | 24 | A4×2 | 43 3*2 |
 |
 |
 |
 |
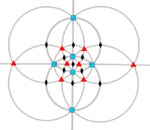
| O (432) |
[4,3]+ | 24 | S4 | 34 43 62 | 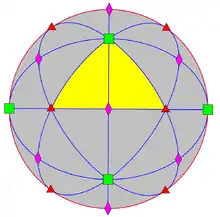 |
 |
 |
 |
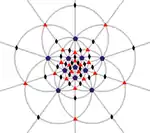
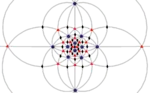
| I (532) |
[5,3]+ | 60 | A5 | 65 103 152 | 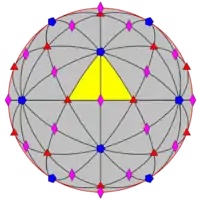 |
 |
 |
 |
Full polyhedral groups
| Weyl Schoe. (Orb.) |
Coxeter notation |
Order | Abstract structure |
Coxeter number (h) |
Mirrors (m) |
Mirror diagrams | |||
|---|---|---|---|---|---|---|---|---|---|
| Orthogonal | Stereographic | ||||||||
| A3 Td (*332) |
[3,3] | 24 | S4 | 4 | 6 |  |  |  |  |
| B3 Oh (*432) |
[4,3] | 48 | S4×2 | 8 | 3 6 |  | 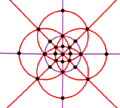 | 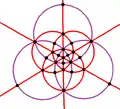 | 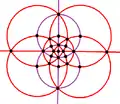 |
| H3 Ih (*532) |
[5,3] | 120 | A5×2 | 10 | 15 |  |  |  |  |
See also
References
- Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, 1973. (The Polyhedral Groups. §3.5, pp. 46–47)