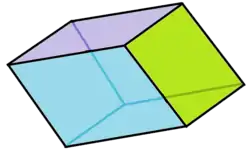
Trigonal trapezohedron
Trigonal trapezohedron
Typetrapezohedron
Conway notationdA3
Coxeter diagram
Faces6 rhombi
Edges12
Vertices8
Face configuration3,3,3,3
Symmetry groupD3d, [2+,6], (2*3), order 12
Rotation groupD3, [2,3]+, (223), order 6
Dual polyhedrontrigonal antiprism
Propertiesconvex, equilateral polygon, face-transitive, zonohedron, parallelohedron

In geometry, a trigonal trapezohedron is a rhombohedron (a polyhedron with six rhombus-shaped faces) in which, additionally, all six faces are congruent. Alternative names for the same shape are the trigonal deltohedron[1] or isohedral rhombohedron.[2] Some sources just call them rhombohedra.[3]

Geometry

Six identical rhombic faces can construct two configurations of trigonal trapezohedra. The acute or prolate form has three acute angle corners of the rhombic faces meeting at the two polar axis vertices. The obtuse or oblate or flat form has three obtuse angle corners of the rhombic faces meeting at the two polar axis vertices.

More strongly than having all faces congruent, the trigonal trapezohedra are isohedral figures, meaning that they have symmetries that take any face to any other face.[3]

Special cases

A cube can be interpreted as a special case of a trigonal trapezohedron, with square rather than rhombic faces.

A gyroelongated triangular bipyramid constructed with equilateral triangles can also be seen as a trigonal trapezohedron when its coplanar triangles are merged into rhombi.

The two golden rhombohedra are the acute and obtuse form of the trigonal trapezohedron with golden rhombus faces. Copies of these can be assembled to form other convex polyhedra with golden rhombus faces, including the Bilinski dodecahedron and rhombic triacontahedron.[4]

Acute golden rhombohedron
Obtuse golden rhombohedron

Four oblate rhombohedra whose ratio of face diagonal lengths are the square root of two can be assembled to form a rhombic dodecahedron. The same rhombohedra also tile space in the trigonal trapezohedral honeycomb.[5]

The trigonal trapezohedra are special cases of trapezohedra, polyhedra with an even number of congruent kite-shaped faces. When this number of faces is six, the kites degenerate to rhombi, and the result is a trigonal trapezohedron. As with the rhombohedra more generally, the trigonal trapezohedra are also special cases of parallelepipeds, and are the only parallelepipeds with six congruent faces. Parallelepipeds are zonohedra, and Evgraf Fedorov proved that the trigonal trapezohedra are the only infinite family of zonohedra whose faces are all congruent rhombi.[3]

Dürer's solid is generally presumed to be a truncated triangular trapezohedron, a trigonal trapezohedron with two opposite vertices truncated, although its precise shape is still a matter for debate.[1]

See also

References

  1. 1 2 Futamura, F.; Frantz, M.; Crannell, A. (2014). "The cross ratio as a shape parameter for Dürer's solid". Journal of Mathematics and the Arts. 8 (3–4): 111–119. doi:10.1080/17513472.2014.974483. MR 3292158.
  2. ↑ Lines, L (1965). Solid geometry: with chapters on space-lattices, sphere-packs and crystals. Dover Publications.
  3. 1 2 3 Grünbaum, Branko (2010). "The Bilinski dodecahedron and assorted parallelohedra, zonohedra, monohedra, isozonohedra, and otherhedra". The Mathematical Intelligencer. 32 (4): 5–15. doi:10.1007/s00283-010-9138-7. hdl:1773/15593. MR 2747698.
  4. ↑ Senechal, Marjorie (2006). "Donald and the golden rhombohedra". The Coxeter Legacy. Providence, Rhode Island: American Mathematical Society. pp. 159–177. MR 2209027.
  5. ↑ Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). The Symmetries of Things. Wellesley, Massachusetts: A K Peters. p. 294. ISBN 978-1-56881-220-5. MR 2410150.
Family of n-gonal trapezohedra
Trapezohedron name Digonal trapezohedron
(Tetrahedron)		 Trigonal trapezohedron Tetragonal trapezohedron Pentagonal trapezohedron Hexagonal trapezohedron Heptagonal trapezohedron Octagonal trapezohedron Decagonal trapezohedron Dodecagonal trapezohedron ... Apeirogonal trapezohedron
Polyhedron image ...
Spherical tiling image Plane tiling image
Face configuration V2.3.3.3 V3.3.3.3 V4.3.3.3 V5.3.3.3 V6.3.3.3 V7.3.3.3 V8.3.3.3 V10.3.3.3 V12.3.3.3 ... V∞.3.3.3


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.