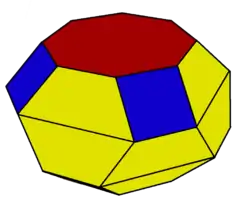
| Truncated square antiprism | |
|---|---|
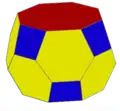 | |
| Type | Truncated antiprism |
| Schläfli symbol | ts{2,8} tsr{4,2} or |
| Conway notation | tA4 |
| Faces | 18: 2 {8}, 8 {6}, 8 {4} |
| Edges | 48 |
| Vertices | 32 |
| Symmetry group | D4d, [2+,8], (2*4), order 16 |
| Rotation group | D4, [2,4]+, (224), order 8 |
| Dual polyhedron | |
| Properties | convex, zonohedron |
The truncated square antiprism one in an infinite series of truncated antiprisms, constructed as a truncated square antiprism. It has 18 faces, 2 octagons, 8 hexagons, and 8 squares.
Gyroelongated triamond square bicupola
If the hexagons are folded, it can be constructed by regular polygons. Or each folded hexagon can be replaced by two triamonds, adding 8 edges (56), and 4 faces (32). This form is called a gyroelongated triamond square bicupola.[1]
Related polyhedra
| Symmetry | D2d, [2+,4], (2*2) | D3d, [2+,6], (2*3) | D4d, [2+,8], (2*4) | D5d, [2+,10], (2*5) |
|---|---|---|---|---|
| Antiprisms |  s{2,4} (v:4; e:8; f:6) |
 s{2,6} (v:6; e:12; f:8) |
 s{2,8} (v:8; e:16; f:10) |
 s{2,10} (v:10; e:20; f:12) |
| Truncated antiprisms |
 ts{2,4} (v:16;e:24;f:10) |
 ts{2,6} (v:24; e:36; f:14) |
 ts{2,8} (v:32; e:48; f:18) |
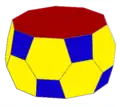 ts{2,10} (v:40; e:60; f:22) |
Snub square antiprism
Although it can't be made by all regular planar faces, its alternation is the Johnson solid, the snub square antiprism.
References
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.