三角形内角的嵌入不等式

注意到不等式：${\displaystyle (x-y\cos C-z\cos B)^{2}+(y\sin C-z\sin B)^{2}\geqslant 0}$ 对所有的实数 x、y、z以及任意角A、B、C成立，将其左侧展开，就得到：

${\displaystyle x^{2}+y^{2}(\cos ^{2}C+\sin ^{2}C)+z^{2}(\cos ^{2}B+\sin ^{2}B)-2xy\cos C-2xz\cos B-2yz\sin B\sin C+2yz\cos B\cos C\geqslant 0}$

${\displaystyle x^{2}+y^{2}+z^{2}\geqslant 2xy\cos C+2xz\cos B+2yz(\sin B\sin C-\cos B\cos C)}$

${\displaystyle x^{2}+y^{2}+z^{2}\geqslant 2xy\cos C+2xz\cos B-2yz\cos(B+C)}$

由于A、B、C是三角形内角，${\displaystyle \cos(B+C)=\cos(\pi -A)=-\cos A}$，因此上式等价于

${\displaystyle x^{2}+y^{2}+z^{2}\geqslant 2xy\cos C+2xz\cos B+2yz\cos A.}$

从证明中可推出，不等式中等号成立当且仅当${\displaystyle y\sin C=z\sin B}$和${\displaystyle x=y\cos C+z\cos B}$同时成立。也就是说，要么${\displaystyle x=y=z=0}$，要么${\displaystyle x:y:z=\sin A:\sin B:\sin C}$。

从以上证明中可以看到，证明成立的关键是${\displaystyle \cos(B+C)+\cos A=0}$，所以可以将条件中的“A、B、C是三角形内角”推广到“${\displaystyle A+B+C=(2k+1)\pi ,\,k\in \mathbb {N} }$”。而如果 ${\displaystyle A+B+C=2k\pi }$，则${\displaystyle \cos(B+C)=\cos A}$，展开恒成立的不等式 ${\displaystyle (x+y\cos C+z\cos B)^{2}+(y\sin C-z\sin B)^{2}\geqslant 0}$便可得到不等式

${\displaystyle x^{2}+y^{2}+z^{2}+2xy\cos C+2yz\cos A+2zx\cos B\geqslant 0.}$

这个不等式和三角形内角的嵌入不等式可以合写成一个不等式[1]：

如果${\displaystyle A+B+C=k\pi ,\,k\in \mathbb {N} }$，那么对任意实数x、y、z，都有${\displaystyle x^{2}+y^{2}+z^{2}+2(-1)^{k}(xy\cos C+yz\cos A+zx\cos B)\geqslant 0.}$

由于三角形内角的嵌入不等式具有高度对称性，在应用中也会写成对称下标不等式：

${\displaystyle x_{1}^{2}+x_{2}^{2}+x_{3}^{2}\geqslant 2x_{1}x_{2}\cos \varphi _{3}+2x_{2}x_{3}\cos \varphi _{1}+2x_{3}x_{1}\cos \varphi _{2}.}$

或轮换下标不等式：

${\displaystyle x_{1}^{2}+x_{2}^{2}+x_{3}^{2}\geqslant 2x_{1}x_{2}\cos \varphi _{1}+2x_{2}x_{3}\cos \varphi _{2}+2x_{3}x_{1}\cos \varphi _{3}.}$

设 ${\displaystyle \alpha _{1},\alpha _{2},\alpha _{3}}$是三角形内角，对后一个不等式做变量代换

${\displaystyle x_{1}\rightarrow x_{1}{\sqrt {\frac {\sin \alpha _{2}}{\sin \alpha _{3}\sin \alpha _{1}}}},\,x_{2}\rightarrow x_{2}{\sqrt {\frac {\sin \alpha _{3}}{\sin \alpha _{1}\sin \alpha _{2}}}},\,x_{3}\rightarrow x_{3}{\sqrt {\frac {\sin \alpha _{1}}{\sin \alpha _{2}\sin \alpha _{3}}}},}$

可以得到不等式[3]：

${\displaystyle (x_{1}^{2}+x_{2}^{2}){\frac {\cos \alpha _{1}}{\sin \alpha _{1}}}+(x_{2}^{2}+x_{3}^{2}){\frac {\cos \alpha _{2}}{\sin \alpha _{2}}}+(x_{3}^{2}+x_{1}^{2}){\frac {\cos \alpha _{3}}{\sin \alpha _{3}}}\geqslant 2x_{1}x_{2}{\frac {\cos \varphi _{1}}{\sin \alpha _{1}}}+2x_{2}x_{3}{\frac {\cos \varphi _{2}}{\sin \alpha _{2}}}+2x_{3}x_{1}{\frac {\cos \varphi _{3}}{\sin \alpha _{3}}}.}$

由这个不等式可以推出嵌入不等式的另一种推广：

设${\displaystyle \alpha _{1},\alpha _{2},\cdots ,\alpha _{n}}$满足 ${\displaystyle \alpha _{1}+\alpha _{2}+\cdots +\alpha _{n}=\pi }$， ${\displaystyle \varphi _{1},\varphi _{2},\cdots ,\varphi _{n}}$满足 ${\displaystyle \varphi _{1}+\varphi _{2}+\cdots +\varphi _{n}=\pi }$，则有：

${\displaystyle \sum _{i=1}^{n}{\frac {\cos \alpha _{i}}{\sin \alpha _{i}}}(x_{i}^{2}+x_{i+1}^{2})\geqslant 2\sum _{i=1}^{n}x_{i}x_{i+1}{\frac {\cos \varphi _{i}}{\sin \alpha _{i}}}.}$

其中${\displaystyle x_{n+1}=x_{1}}$。而当${\displaystyle \alpha _{1}=\alpha _{2}=\cdots =\alpha _{n}={\frac {\pi }{n}}}$的时候，上面的不等式转化为：

${\displaystyle \cos {\frac {\pi }{n}}\sum _{i=1}^{n}(x_{i}^{2}+x_{i+1}^{2})\geqslant 2\sum _{i=1}^{n}x_{i}x_{i+1}\cos \varphi _{i}.}$

嵌入不等式是此不等式在${\displaystyle n=3}$时的特例[3]。

三角形内角的嵌入不等式将代数不等式和几何不等式结合起来[3]。运用嵌入不等式可以解决许多几何不等式[1]，例如以下是运用嵌入不等式证明埃尔德什－莫德尔不等式。

${\displaystyle r_{3}}$（红）小于${\displaystyle w_{3}}$（蓝）.

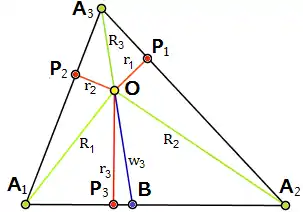
埃尔德什-莫德尔不等式是一个二十世纪初期发现的不等式，其声称：对于任何三角形和其内部的一点O，点O到三角形三条边的距离之和总是小于或等于点O到三角形的三个顶点的距离之和的一半。下设这个三角形顶点为${\displaystyle A_{1},A_{2},A_{3}}$，点O到这三个顶点的距离分别是${\displaystyle R_{1},R_{2},R_{3}}$，到它们对边的距离分别是${\displaystyle r_{1},r_{2},r_{3}}$，则埃尔德什-莫德尔不等式写作：

${\displaystyle R_{1}+R_{2}+R_{3}\geqslant 2\left(r_{1}+r_{2}+r_{3}\right)}$

在嵌入不等式中令${\displaystyle x={\sqrt {R_{1}}},y={\sqrt {R_{2}}},z={\sqrt {R_{3}}}}$，${\displaystyle A={\frac {\angle A_{2}OA_{3}}{2}},B={\frac {\angle A_{1}OA_{3}}{2}},C={\frac {\angle A_{1}OA_{2}}{2}}}$则可得到：

${\displaystyle R_{1}+R_{2}+R_{3}\geqslant 2\left[{\sqrt {R_{1}R_{2}}}\cos \left({\frac {\angle A_{1}OA_{2}}{2}}\right)+{\sqrt {R_{2}R_{3}}}\cos \left({\frac {\angle A_{2}OA_{3}}{2}}\right)+{\sqrt {R_{1}R_{3}}}\cos \left({\frac {\angle A_{1}OA_{3}}{2}}\right)\right]}$

另一方面，计算三角形${\displaystyle A_{1}OA_{2}}$在O点发出的角平分线长度${\displaystyle w_{3}}$，可得

${\displaystyle w_{3}={\frac {2R_{1}R_{2}}{R_{1}+R_{2}}}\cos \left({\frac {\angle A_{1}OA_{2}}{2}}\right)\leqslant {\sqrt {R_{1}R_{2}}}\cos \left({\frac {\angle A_{1}OA_{2}}{2}}\right).}$

同时作为角平分线，其长度必然大于O点到${\displaystyle A_{1}A_{2}}$的距离${\displaystyle r_{3}}$，所以

${\displaystyle r_{3}\leqslant w_{3}\leqslant {\sqrt {R_{1}R_{2}}}\cos \left({\frac {\angle A_{1}OA_{2}}{2}}\right)}$

${\displaystyle r_{1}+r_{2}+r_{3}\leqslant {\sqrt {R_{1}R_{2}}}\cos \left({\frac {\angle A_{1}OA_{2}}{2}}\right)+{\sqrt {R_{2}R_{3}}}\cos \left({\frac {\angle A_{2}OA_{3}}{2}}\right)+{\sqrt {R_{1}R_{3}}}\cos \left({\frac {\angle A_{1}OA_{3}}{2}}\right)}$

因此

${\displaystyle R_{1}+R_{2}+R_{3}\geqslant 2\left(r_{1}+r_{2}+r_{3}\right).}$[4]

设 ${\displaystyle A+B+C=k\pi }$, ${\displaystyle k\in \mathbb {Z} }$, ${\displaystyle x,y,z\in \mathbb {R} }$，则有

${\displaystyle (x+y+z)^{2}\geqslant 4yz\sin ^{2}A+4zx\sin ^{2}B+4xy\sin ^{2}C,}$

等号成立当且仅当 ${\displaystyle x:y:z=\sin 2A:\sin 2B:\sin 2C}$。[5][6][7]

• 三角不等式
• 外森比克不等式