不稳定性

控制理論中的穩定性有幾種不同的定義，最常見的是有界輸入有界輸出穩定性，有一個系統在有限大小的輸入（有界輸入）時都有有限大小的輸出（有界輸出），系統即為穩定。

若一個線性時不變系統其特徵方程式有實部大於零的根，或有實部為零的重根，此系統即為不穩定系統，這也相當於其狀態矩陣有特徵值的實部大於零。

• 挫曲：細長物體在受到較大壓力時，會因受力而彎曲，因此物體會在應力到達强度之前就因變形而損壞。
• Drucker穩定性：一些應力及應變之間的非線性關係。
• Biot不穩定性（Biot instability）：弹性体的表面起皺
• Baroclinic不穩定性[2]。

瑞利－泰勒不穩定性的流體力學模擬[3]

兩個衝擊射流碰撞產生的不穩定流結構

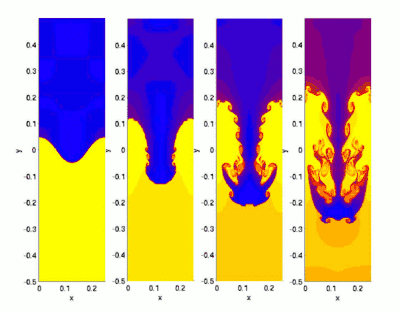
流體不穩定性會出現在液態、氣態及電漿態。在流體動力學及磁流動力學中會研究不穩定性，流體不穩定性會包括以下的幾種：

• 磁层中出現的气球不稳定性（類似瑞利－泰勒不穩定性）
• 大氣不穩定性
  • 流体动力不稳定性（大氣動力學）
    • 慣性不穩定性（Inertial instability）、克耳文-亥姆霍茲不穩定性、對稱不穩定性（symmetric instability）、条件性对称不稳定性（conditional symmetric instability）或對流對稱不穩定性（convective symmetric instability）、正壓不穩定性（barotropic instability）、旋轉不穩定性（rotational instability）
  • 流體靜力不穩定性或熱力學不穩定性 (大氣熱力學)
    • 條件不穩定性（Conditional instability）或靜不穩定性（static instability）、浮力不穩定性（buoyant instability）、對流不穩定性、絕對不穩定性（absolute instability）
• 瑞立-貝納對流
• 漂移磁镜模不稳定性（Drift mirror instability）
• 布魯托─雷利不穩定性（類似電漿的Diocotron不稳定性，但不一樣）
• 瑞利－泰勒不穩定性
• 普拉托-瑞利不稳定性（類似瑞利－泰勒不穩定性）
• 里克特迈耶－梅什科夫不稳定性（類似瑞利－泰勒不穩定性）
• 激波不穩定性

若一星系或星团其重力位的擾動會造成密度改變，再增強重力位的擾動，此星系或星团即為不穩定的。這類的不穩定性需要和恆星的移動相當相關，因此擾動不會被隨機運動所淡化。若系統出現不稳定性後，系統一般會比原來更「熱」（隨機性更高），恆星系統的穩定性有：

• 快速旋轉圓盤的棒状不稳定性。
• 金斯不稳定性：恆星形成時，當分子雲的熱壓力不足以抵抗引力時，會在引力的作用下發生塌縮。
• 水龍軟管不穩定性[4]。
• 重力熱力學不穩定性（Gravothermal instability）
• 径向轨道不稳定性（Radial-orbit instability）
• 冷旋轉圓盤的各種不穩定性。

關節不穩定是身體扭傷後最常見的後遺症。力學性的不穩定包括不足的穩定結構以及超過肢體限制的活動性。機能性的不穩定包括受傷關節反覆的扭傷[5]。受傷導致肌肉運動知覺的缺陷及受損的關節姿勢控制。肌肉無力、潛在不穩定、姿勢控制能力減退的人比平常人更容易受傷。不穩定性會導致重心擺動（postural sway）的增加，量測方式是量測個人偏離理想壓力中心的時間及距離。壓力中心的定義是重心對地的投影位置。研究者有提出理論，若關節受傷有導致傳入神經阻滯、感覺神經纖維的中斷、及機能上的不穩定，會影響其重心擺動[6]。關節的穩定性可以用外部支持系統或是調整肢體的力學來改善，支架提供的力學支撐可以維持姿勢控制，並且增加穩定性。

• 電漿不穩定性
• 稳定-不稳定悖论
• 失敗國家：政治的不穩定性
• 不穩定對超新星
• 白克蘭電流