五十九種二十面體
《五十九種二十面體》(英語:)是一本由哈羅德·斯科特·麥克唐納·考克斯特、帕特里克·杜·瓦爾、H·T·夫雷勒和J·F·皮特里撰寫的主題為星形二十面體的數學書籍,書中依據杰弗裡·查爾斯·珀西·米勒提出的一組規則列出並介紹一些與柏拉圖正二十面體及相關凸正圖形有關連的星形多面體[1][2]。
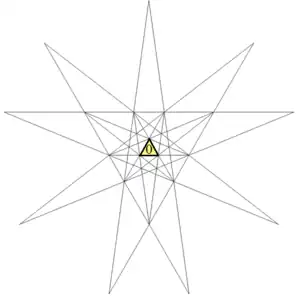
星狀圖中間的三角形代表了原始的二十面體
這本書最早由多倫多大學於1938年出版[1],第二版由施普林格出版社發行,隨後於1982年K和D·克內尤以相同文字重新排版、繪圖增加圖表和新的參考資料和照片,並修訂為塔奎的第三版[3],於1999年出版。
作者的貢獻
米勒的規則
雖然米勒對這本書沒有直接的貢獻,但他與考克斯特和皮特里是往來密切的同事。他的貢獻是他提出一套規則能從無限多種星形多面體中明確的定義出那些星形多面體是「重要且特別」的[1]:
考克斯特
考克斯特是推動本書完成的主要力量。他將已知的資料用一些方法比如組合數學和抽象的圖論以及當時被用在小說中的幾何環境以米勒的規則為基礎進行分析。

他觀察星座圖的許多線段,然後設計出了一個演算法來以米勒的規則控制相鄰平面區域的組合,來列舉出所有符合米勒規則的星形二十面體組合[9]。
他繪製的圖顯示了個個確定連通的面。不同希臘字母代表可以替換的部分:
- λ 可能為 3 或 4
- μ 可能為 7 或 8
- ν 可能為 11 或 12
派屈克·杜·瓦爾
帕特里克·杜·瓦爾藉由觀察各種星形二十面體位於“殼”的周圍的原始二十面體而設計了一種適合表達星形二十面體各個胞的符號表示法。並在這個基礎上測試米勒的規則可得到的所有可能的組合,並更加確定了考克斯特所使用的分析方法結果。
參見
- 溫尼爾二十面體模型列表 – 溫尼爾的書 《多面體模型》中收錄了21種星形二十面體
- 二十面體對稱的多面體列表
- 星形二十面體列表
參考文獻
- Guy's. . steelpillow.com. 2010-12-19 [2016-03-26]. (原始内容存档于2016-03-04).
- Hart, G. . [2016-03-12]. (原始内容存档于2020-01-22).
- Allanson, B. . [2016-03-25]. (原始内容存档于2019-12-28).
- . paulscottinfo.ipage.com. [2016-03-25]. (原始内容存档于2019-12-27).
- . maplesoft.com. [2020-12-15]. (原始内容存档于2020-10-25).
- H. S. M. Coxeter, P. Du Val, H. T. Flather, J. F. Petrie. . SpringerLink. [2018-04-02]. doi:10.1007/978-1-4613-8216-4 (英国英语).
- Ha Le. . Centre for Experimental and Constructive Mathematics. 1998-11-17 [2016-03-26]. (原始内容存档于2019-09-08).
- Robert Webb. . software3d.com. [2016-03-25]. (原始内容存档于2020-10-23).
- Coxeter, H. S. M.; Du Val, P.; Flather, H. T.; and Petrie, J. F. The Fifty-Nine Icosahedra. Stradbroke, England: Tarquin Publications, 1999.
- Brückner, Max (1900). Vielecke und Vielflache: Theorie und Geschichte. Leipzig: B.G. Treubner. ISBN 978-1-4181-6590-1. (德文)
- WorldCat(页面存档备份,存于) English: Polygons and Polyhedra: Theory and History. Photographs of models: Tafel VIII (Plate VIII), etc. High res. scans.(页面存档备份,存于)
- H. S. M. Coxeter, Patrick du Val, H.T. Flather, J.F. Petrie (1938) The Fifty-nine Icosahedra, University of Toronto studies, mathematical series 6: 1–26.
- Wenninger, Magnus J. (1983) Polyhedron models; Cambridge University Press, Paperback edition (2003). ISBN 978-0-521-09859-5.
- A. H. Wheeler (1924) "Certain forms of the icosahedron and a method for deriving and designating higher polyhedra", Proceedings of the International Congress of Mathematicians, Toronto, Vol. 1, pp 701–708.
外部連結
- Example stellations of the icosahedron(页面存档备份,存于)
- The fifty nine stellations of the regular icosahedron
- 埃里克·韦斯坦因. . MathWorld.
- Stellations of the icosahedron
- George Hart, 59 Stellations of the Icosahedron(页面存档备份,存于) - VRML 3D files.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.