二十面體對稱的多面體列表
下表列出了屬於二十面體對稱的均勻多面體。
完全二十面體對稱的多面體
{5,3} |
{3,5} |
3.10.10 |
 4.6.10 |
 5.6.6 |
 3.4.5.4 |
 3.5.3.5 |
卡塔蘭立體 - 阿基米德立體的對偶多面體
 V3.10.10 |
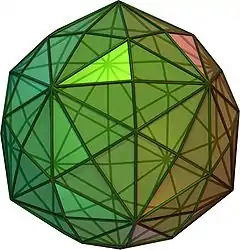 V4.6.10 |
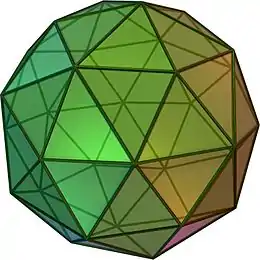 V5.6.6 |
V3.4.5.4 |
 V3.5.3.5 |
阿基米德立體
| 名稱 | 圖像 | 面 | 邊 | 頂點 | 頂點布局 | |
|---|---|---|---|---|---|---|
| 截半二十面體 (擬正: 頂角與邊等價) |
 (旋轉模型) |
32 | 20個正三角形 12個正五邊形 |
60 | 30 | 3,5,3,5 |
| 截角十二面體 | (旋轉模型) |
32 | 20個正三角形 12個正十邊形 | 90 | 60 | 3,10,10 |
| 截角二十面體 或足球 |
 (旋轉模型) |
32 | 12個正五邊形 20個正六邊形 | 90 | 60 | 5,6,6 |
| 小斜方截半二十面體 或小大斜方截半二十面體 |
 (旋轉模型) |
62 | 20個正三角形 30個正方形 12 正五邊形 |
120 | 60 | 3,4,5,4 |
| 大斜方截半二十面體 或大小斜方截半二十面體 |
 (旋轉模型) |
62 | 30個正方形 20個正六邊形 12個正十邊形 |
180 | 120 | 4,6,10 |
卡塔蘭立體
| 名稱 | 圖像 | 對偶 | 面 | 邊 | 頂點 | 面的形狀 |
|---|---|---|---|---|---|---|
| 菱形三十面體 (擬正多面體的對偶) |
 (旋轉模型) |
截半二十面體 | 30 | 60 | 32 | 菱形 |
| 三角化二十面體 |  (旋轉模型) |
截角十二面體 | 60 | 90 | 32 | 等腰三角形 |
| 五角化十二面體 |  (旋轉模型) |
截角二十面體 | 60 | 90 | 32 | 等腰三角形 |
| 鳶形六十面體 | (旋轉模型) |
小斜方截半二十面體 | 60 | 120 | 62 | 箏形 |
| 四角化菱形三十面體 |  (旋轉模型) |
大斜方截半二十面體 | 120 | 180 | 62 | 不等邊三角形 |
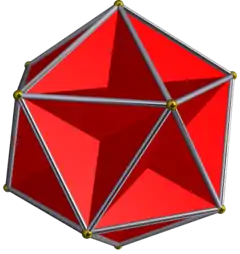
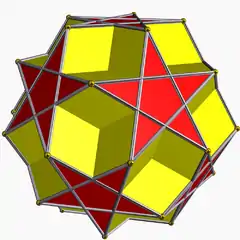
克普勒-普安索立體
非凸均勻多面體
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
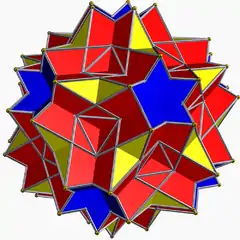 |
 |
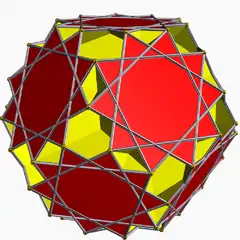 |
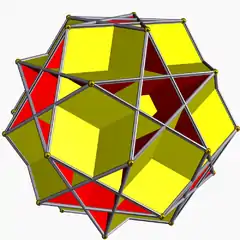 |
 |
 |
 |
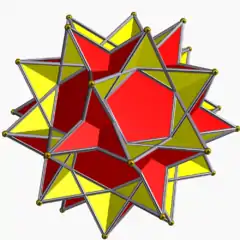 |
 |
 |
 |
 |
 |
 |
手性的阿基米德和卡塔蘭立體
| 名稱 | 圖像 | 面 | 邊 | 頂點 | 頂點布局 | |
|---|---|---|---|---|---|---|
| 扭棱十二面體 或扭棱截半二十面體 (2種手性鏡像) |
 (旋轉模型)  (旋轉模型) |
92 | 80個三角形 12個五邊形 | 150 | 60 | 3,3,3,3,5 |
| 名稱 | 圖像 | 對偶 | 面 | 邊 | 頂點 | 面的形狀 |
|---|---|---|---|---|---|---|
| 五角六十面體 (2種手性鏡像) |
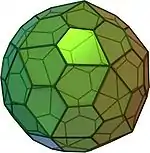 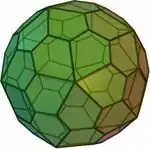 (旋轉模型)(旋轉模型) |
扭棱十二面體 | 60 | 50 | 92 | 不等邊五邊形 |
手性的非凸均勻多面體
 |
 |
 |
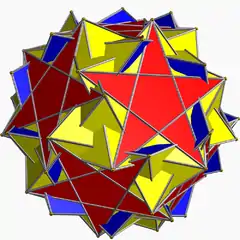 |
 |
 |
 |
參考文獻
- Klein, F. [On the order-seven transformation of elliptic functions]. Mathematische Annalen. 1878, 14 (3): 428–471. doi:10.1007/BF01677143. Translated in Levy, Silvio (编). . Cambridge University Press. 1999 [2016-03-13]. ISBN 978-0-521-66066-2. MR 1722410. (原始内容存档于2010-08-23). (页面存档备份,存于)
- Klein, F., , Mathematische Annalen, 1879, 15 (3-4): 533–555, doi:10.1007/BF02086276, collected as pp. 140–165 in Oeuvres, Tome 3
- Klein, Felix, , Trübner & Co., 1888, ISBN 0-486-49528-0trans. George Gavin Morrice
- Tóth, Gábor, , 2002
- Peter R. Cromwell, Polyhedra (1997), p.296
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 (页面存档备份,存于)
- N.W. Johnson: Geometries and Transformations, (2015) Chapter 11: Finite symmetry groups
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.


























































