光子计算机

光子计算机（亦称光脑）是指以光子替代电子的先进计算机。數十年來的研究指出，光子可以比傳統電腦中使用的电子有更高的頻寬（例如光纖）。

大多数研究项目都专注于用光学等效模組替换当前的计算机组件，目的是要得到可以处理二进制数据的光学计算机系统。这种方法似乎为商业光学计算提供了最佳的短期前景，因为光学组件可以集成到传统计算机中，形成光电混合的系統。然而，光电设备因為将电能转换为光能再轉回電能，會損失30％的能量。此转换也会减慢消息的传输速度。全光学计算机不需要光学-电学-光学（OEO）转换，因此减少了对电力的需求[1]。

有些应用的设备，像是合成孔径雷达（SAR）和光学相关器，已可以用光学计算的原理來設計。例如可以使用相关器来检测和跟踪对象[2]，并对串行时域光学数据进行分类[3]。

二进制数字计算机的光学元件

现代电子计算机的基本构件是晶体管。为了用光学元件取代电子元件，需要一个相当的光学晶体管。这需要使用具有非线性折射率的材料来实现。特别是，存在一些材料[4]，在这些材料中，入射光的强度以类似于双极晶体管的电流响应的方式影响通过该材料传输的光的强度。这种光学晶体管[5][6]可用于制造光学逻辑门，[6]而这些光学门又被组装成计算机中央处理器（CPU）的高级部件。这些将是非线性光学晶体，用于操纵光束以控制其他光束。

像任何计算系统一样，光学计算系统需要三样东西才能良好运作。

  1. 光学处理器
  2. 光学数据传输，例如光纤电缆
  3. 光存储[7]

代替电气元件需要将数据格式从光子转换为电子，这将使系统变得更慢。

争论

对于光学计算机的未来能力，研究人员之间存在一些分歧；它们是否可能在速度、功耗、成本和尺寸方面与基于半导体的电子计算机竞争，是一个开放的问题。批评者指出[8]现实世界的逻辑系统需要 "逻辑级恢复、级联性、扇出和输入输出隔离"，所有这些目前都由电子晶体管以低成本、低功率和高速度提供。为了使光逻辑在少数利基应用之外具有竞争力，需要在非线性光器件技术方面取得重大突破，或者也许需要改变计算本身的性质。 [9]

误解、挑战和前景

光计算的一个重大挑战是，计算是一个非线性过程，其中多个信号必须相互作用。光是一种电磁波，只有在材料中存在电子的情况下才能与另一种电磁波互动，[10]而这种互动的强度对于电磁波，比如光，比传统计算机的电子信号要弱得多。这可能导致光学计算机的处理元件比使用晶体管的传统电子计算机需要更多的功率和更大的尺寸。。

另一个误解是，由于光的速度比电子的漂移速度快得多，而且频率以THz为单位，所以光学晶体管应该能够实现极高的频率。然而，任何电磁波都必须遵守转换极限，因此，光晶体管对信号的响应速度仍受其光谱带宽的限制。在光纤通信中，诸如色散等实际限制往往将信道的带宽限制在10几兆赫，只比许多硅晶体管略好。因此，要想获得比电子晶体管更快的运行速度，就需要采用实用的方法，将超短脉冲沿着高色散波导传输。

光子逻辑
Realization of a photonic controlled-NOT gate for use in quantum computing

光子逻辑是在逻辑门中使用光子（光）（NOT、AND、OR、NAND、NOR、XOR、XNOR）。当两个或更多的信号结合在一起时，使用非线性光学效应获得开关。[6]

谐振器在光子逻辑中特别有用，因为它们允许从建设性干涉中积累能量，从而增强光学非线性效应。

其他已被研究的方法包括在分子水平的光子逻辑，使用光致发光化学品。在一次演示中，Witlicki等人利用分子和SERS进行了逻辑运算。[11]

非常规方法

时间延迟光学计算

其基本思想是延迟光（或任何其他信号）以进行有用的计算。[12] 令人感兴趣的是解决NP完全问题，因为这些问题对传统计算机来说是很困难的。

在这种方法中实际使用了光的2个基本特性。

  • 光可以通过一定长度的光纤而被延迟。
  • 光可以被分割成多条（子）光线。这一特性也是至关重要的，因为我们可以在同一时间内评估多个解决方案。

当解决一个有时间延迟的问题时，必须遵循以下步骤。

  • 第一步是创建一个由光缆和分割器组成的图状结构。每个图都有一个起始节点和一个目的节点。
  • 光线从起始节点进入并穿越图形，直到到达目的地。在通过弧线时，它会被延迟，并在节点内部被分割。
  • 光线在通过弧线或节点时被标记，这样我们就可以在目的地节点轻松地识别这一事实。
  • 在目的地节点，我们将等待在某一（些）特定时刻到达的信号（信号强度的波动）。如果在那一刻没有信号到达，这意味着我们的问题没有解决方案。否则，问题就有了解决方案。波动可以用一个光电探测器和一个示波器来读取。

第一个以这种方式攻击的问题是哈密顿路径问题。[12]。

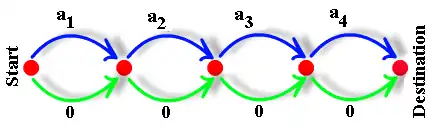
最简单的是子集和问题。[13] 一个解决有4个数字{a1, a2, a3, a4}的实例的光学装置被描述如下。

Optical device for solving the Subset sum problem。

光线将进入开始节点。它将被分成2条强度较小的（子）光线。这两条光线将在a1和0的时刻到达第二个节点。 将在0、a1、a2和a1+a2的时刻到达第三个节点。这些代表了集合{a1, a2}的所有子集。我们期望信号的强度在不超过4个不同时刻出现波动。在目的节点，我们期望波动不超过16个不同的时刻（这是给定的所有子集）。如果我们在目标时刻B有波动，就意味着我们有问题的解决方案，否则就没有元素之和等于B的子集。对于实际执行，我们不可能有零长度的电缆，因此所有的电缆都增加了一个小的（对所有的固定）值k。在这种情况下，预计解决方案在时刻B+n*k。

基于波长的计算

基于波长的计算[14]可以用来解决3-SAT问题，该问题有n个变量，m个条款，每个条款的变量不超过3个。每一个波长，包含在一条光线中，被认为是对n个变量的可能赋值。[15]

通过在透明胶片上施胶来计算

这种方法使用施乐机和透明片进行计算。[16] k-SAT问题有n个变量，m个子句，每个子句最多有k个变量，已分3步解决：[17]

  • 首先通过进行n次施胶拷贝，产生了n个变量的所有2^n次可能的分配。
  • 使用最多 2k 份真值表，每个条款同时在真值表的每一行进行评估。
  • 通过对所有m个子句的重叠透明片进行一次拷贝操作，就可以得到解。

Shaked等人（2007）已经解决了旅行推销员问题[18] by using an optical approach. 所有可能的TSP路径都已生成并存储在一个二进制矩阵中，该矩阵与另一个包含城市间距离的灰度向量相乘。乘法是通过使用一个光学相关器以光学方式进行的。

光学傅里叶协处理器

许多计算，特别是科学应用，需要经常使用二维离散傅里叶变换（DFT）--例如，在解决描述波的传播或热的传递的微分方程时。尽管现代GPU技术通常能够高速计算大型二维DFT，但已经开发出的技术可以通过利用自然的镜头的傅里叶变换特性来进行连续傅里叶变换。输入是通过一个液晶空间光调制器进行编码的。空间光调制器对输入进行编码，并使用传统的CMOS或CCD图像传感器测量结果。由于光学传播固有的高度互连性质，这种光学架构可以提供卓越的计算复杂性扩展，并已被用于解决二维热方程。[19]

伊辛机

设计灵感来自于理论易辛模型的物理计算机被称为Ising机。[20][21][22]

山本义久在斯坦福大学的实验室率先使用光子建造伊辛机。最初，山本和他的同事使用激光器、镜子和其他在光学台上常见的光学元件建造了一台伊辛机。[20][21]

后来，惠普实验室的一个团队开发了光子集成电路设计工具，并利用这些工具在单个芯片上建立了一台伊辛机，在该单个芯片上集成了1052个光学元件。[20]。

另见

参考
  1. Nolte, D.D. . Simon and Schuster. 2001: 34 [2019-12-10]. ISBN 978-0-7432-0501-6. （原始内容存档于2017-01-18）.
  2. Feitelson, Dror G. . . Cambridge, Massachusetts: MIT Press. 1988. ISBN 978-0-262-06112-4.
  3. Kim, S. K.; Goda, K.; Fard, A. M.; Jalali, B. . Optics Letters. 2011, 36 (2): 220–2. Bibcode:2011OptL...36..220K. PMID 21263506. doi:10.1364/ol.36.000220.
  4. . [2022-12-06]. （原始内容存档于2021-03-07）.
  5. Jain, K.; Pratt, G. W. Jr. . Appl. Phys. Lett. 1976, 28 (12): 719. Bibcode:1976ApPhL..28..719J. doi:10.1063/1.88627.
  7. . Microsoft Research. [2019-11-07]. （原始内容存档于2022-10-13） （美国英语）.
  8. Tucker, R.S. . Nature Photonics. 2010, 4 (7): 405. Bibcode:2010NaPho...4..405T. doi:10.1038/nphoton.2010.162.
  9. Rajan, Renju; Babu, Padmanabhan Ramesh; Senthilnathan, Krishnamoorthy. . Photonics. Photonics Spectra. [2018-04-08]. （原始内容存档于2023-02-10）.
  10. Philip R. Wallace. . 1996. ISBN 978-0387946597.
  11. Witlicki, Edward H.; Johnsen, Carsten; Hansen, Stinne W.; Silverstein, Daniel W.; Bottomley, Vincent J.; Jeppesen, Jan O.; Wong, Eric W.; Jensen, Lasse; Flood, Amar H. . J. Am. Chem. Soc. 2011, 133 (19): 7288–91. PMID 21510609. doi:10.1021/ja200992x.
  12. Oltean, Mihai. . Unconventional Computing. Springer LNCS 4135: 217–227. 2006. arXiv:0708.1496 可免费查阅. doi:10.1007/11839132_18.
  13. Mihai Oltean, Oana Muntean. . Natural Computing. 2009, 8 (2): 321–331. S2CID 869226. arXiv:0708.1964 可免费查阅. doi:10.1007/s11047-007-9059-3.
  14. Sama Goliaei, Saeed Jalili. . Optical SuperComputing Workshop: 77–85. 2009. Bibcode:2009LNCS.5882...77G. doi:10.1007/978-3-642-10442-8_10.
  15. Bartlett, Ben; Dutt, Avik; Fan, Shanhui. . Optica. 2021-12-20, 8 (12): 1515–1523. Bibcode:2021Optic...8.1515B. ISSN 2334-2536. arXiv:2101.07786 可免费查阅. doi:10.1364/OPTICA.424258 （英语）.
  16. Head, Tom. . Algorithmic Bioprocesses. Springer: 631–637. 2009. doi:10.1007/978-3-540-88869-7_31.
  17. , [2022-08-14], （原始内容存档于2019-08-10） （英语）
  18. NT Shaked, S Messika, S Dolev, J Rosen. . 应用光学. 2007, 46 (5): 711–724. Bibcode:2007ApOpt..46..711S. PMID 17279159. S2CID 17440025. doi:10.1364/AO.46.000711.
  19. A. J. Macfaden, G. S. D. Gordon, T. D. Wilkinson. . 科学报告. 2017, 7 (1): 13667. Bibcode:2017NatSR...713667M. PMC 5651838 可免费查阅. PMID 29057903. doi:10.1038/s41598-017-13733-1.
  20. Courtland, Rachel. . IEEE Spectrum. 2017年1月2日 [2019年7月16日]. （原始内容存档于2021年4月19日）.
  21. Cartlidge, Edwin. . Physics World. 2016年10月31日 [2019年7月16日]. （原始内容存档于2018年2月23日）.
  22. Cho, Adrian. . Science. 2016-10-20 [2022-12-06]. （原始内容存档于2022-10-09）.

延伸阅读

外部链接
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.