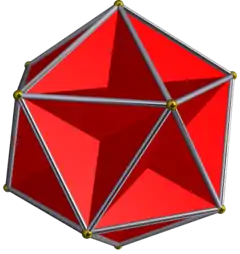
凹凸性 (幾何)
在几何学中，一个幾何圖形可分为凸或凹的。例如多邊形和多面體。其中，凸的多邊形稱為凸多邊形、凹的多邊形則可稱為凹多邊形或非凸多邊形，多面體與多胞體亦然。然而在三維或更高維度的空間中，不是凸的幾何圖形不一定會是凹幾何圖形，亦可能是星形幾何圖形，因此在三維或更高維度的空間中較常分為凸與非凸。
凸幾何圖形
凸幾何圖形是指内部为凸集的幾何圖形[1]，二維空間中的凸幾何圖形稱為凸多邊形、三維空間則稱凸多面體。若一多胞形的内部为凸集，則稱凸多胞形。
二維空間中的凸幾何圖形稱為凸多邊形，简单多边形的下列性质与其凸性等价：
凸幾何圖形的凸包與其邊界相同。
凹幾何圖形
凹幾何圖形是指内部不是凸集的幾何圖形，在二維空間中，不是凸集的簡單多邊形，稱為凹多边形（Concave polygon）[2]或凹角[3]。
凹多邊形至少存在一個內角大於180度。
在三維空間中，不是凸的幾何圖形不一定會是凹幾何圖形，亦可能是星形多面體，因此在三維空間中較常分為凸與非凸。
凹多边形示例
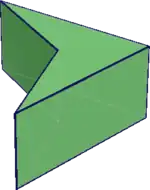凹多面體示例：凹鷂形柱
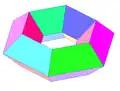環形多面體
嚴格凸與非嚴格凸
非嚴格凸的正三角錐反角柱，其由一個正三角錐和一個三角反角柱組成，上方的三角錐側面與三角反角柱側面共面，而非严格小于180度。
如果一个简单多边形的每个内角严格小于180度，是严格凸的；如果每个非相邻顶点间的线段除端点外严格位于多边形的内部，也是严格凸的。
所有非退化三角形都是严格凸的。
星形幾何圖形
星形幾何圖形是非凸幾何圖形的一個特例，其並未有一個明確的定義。在二維空間中，稱為星形多邊形，數學家Branko Grünbaum指出了兩種由克普勒提出的定義：一種是具有自相交稜的正星形多邊形，且自相交的稜不產生新的頂點，另一種是邊可遞的簡單凹多邊形[4]。
參見
- 凹多邊形
- 凸多邊形
参考文献
- . [2009-10-18]. （原始内容存档于2017-10-17）.
- McConnell, Jeffrey J., : 130, 2006, ISBN 0763722502.
- Mason, J. I., , The Mathematical Gazette, 1935, 30 (291): 237–238 [2009-10-18], （原始内容存档于2016-03-25）.
- Grünbaum & Shephard 1987，section 2.5
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.