分子结构

分子结构，或称分子立体结构、分子形状、分子几何、分子几何构型，建立在光谱学数据之上，用以描述分子中原子的三维排列方式。分子结构在很大程度上影响了化学物质的反应性、极性、相态、颜色、磁性和生物活性。[1][2][3]

水分子结构

分子结构最好在接近绝对零度的温度下测定，因为随着温度升高，分子转动也增加。量子力学和半实验的分子模拟计算可以得出分子形状，固态分子的结构也可通过X射线晶体学测定。体积较大的分子通常以多个稳定的构象存在，势能面中这些构象之间的能垒较高。

分子结构涉及原子在空间中的位置，与键结的化学键种类有关，包括键长、键角以及相邻三个键之间的二面角。

温度对其的影响

由于分子中原子的运动由量子力学决定，因此“运动”这个概念也必须要建立在量子力学基础之上。总体（外部）的量子力学运动——如平移和旋转几乎不改变分子的结构（由旋转导致的科里奥利力和离心扭曲以及由此导致的形状变化在此可以忽略）。内部运动包括振动，隶属于谐波，即原子即使在绝对零度仍会在平衡间振荡。此时所有原子都处于振动基态，具有零点能量，振动模式的波函数也不是一个尖峰，而是有限宽度的指数。随着温度升高，振动模式（自由度）被热激发，用通俗的话讲是分子振动加快，而它们仍然只在分子特定部分振荡。

玻尔兹曼分布可以量度温度对分子振动的影响： $\exp \left(-{\frac {\Delta E}{kT}}\right)$ ，其中 $\Delta E$ 是振动模式的激发能， $k$ 是玻尔兹曼常数， $T$ 是绝对温度。在298K（25 °C）下，典型的玻尔兹曼因子值为：ΔE = 500 cm^-1 → 0.089；ΔE = 1000 cm^-1 → 0.008；ΔE = 1500 cm^-1 → 7 * 10^-4。即，如果激发能为500 cm^-1，那么大约9%的分子在室温时会处于热激发态。对水分子而言，其弯曲模式具有最低的激发能，大约为1600 cm^-1，因此室温下水分子中振动速度比绝对零度时快的分子占不到0.07%。

虽然转动很难影响分子结构，但作为一个量子力学运动，相对振动而言它在低温下热激发程度较高。从经典力学角度来看即是，更多分子在高温下转动更快（它们具有更大的角速度和角动量）；而从量子力学角度看则是，随温度升高，更多角动量较大的本征态开始聚集。典型的转动激发能数量级在几cm^-1。

由于涉及转动态，很多光谱学的实验数据都被扩大了。而转动运动随温度升高而变得激烈，因此，低温下的分子结构数据往往更加可靠，而从高温下的光谱很难得出分子结构。

成键

根据定义，分子中的原子是由共价键连结起来的，包括单键、双键、叁键等（另一种原子的成键方法被成为离子键，并且涉及一个正的阳离子和一个负的阴离子）。

因此分子形状可通过键长、键角和二面角这些参数来阐明。键长被定义为任何分子中，两个原子中心间的平均距离；键角是相邻三个原子两条键之间的夹角；而二面角，或称扭转角，则相对于四个相邻原子而言，是前三个原子所形成的平面与剩下一根键之间所成的角度。

电子的量子力学性质决定分子结构，因此可通过价键理论近似来理解化学键类型对结构的影响。杂化轨道理论认为，先有原子轨道间的杂化，才有化学键的生成。至于化学键，其中两种最常见的为σ键和π键，而含离域电子的结构可借助分子轨道理论来理解。

研究原子和分子中电子的类波行为隶属于量子化学的范畴。

异构体

具有相同化学式但不同结构的物质被称为异构体，它们常有不同的性质。

纯净物只由异构体中的一种构成，因此所有分子结构相同。
結構异构体中原子排列顺序不同，性质也常有不同，例如正丙醇和异丙醇。
- 官能团异构体是由于含有不同官能团而导致异构的异构体，例如醚和醇。
立体异构体物理性质可能类似（例如熔点和沸点），但生化活性一般不同。这是由于它们具有手性，必须要有特定的立体结构才可以与其他底物结合。一对立体异构体可使偏振光偏转相同的角度，但是在相反方向上。
蛋白质折叠关系到高分子蛋白质的构象取向问题。

分子结构类型

分子有六种基本形状类型：

直线型：所有原子处在一条直线上，键角为180°，例如二氧化碳 ${\ce {O=C=O}}$ 。
平面三角形：所有原子处在一个平面上，三个周边原子均匀分布在中心原子周围，键角120°，例如三氟化硼 ${\ce {BF3}}$ 。
四面体：四个周边原子处在四面体的四个顶点，中心原子位于四面体中心。理想键角 $\arccos {-{\frac {1}{3}}}\approx 109^{\circ }28'$ ，例如甲烷 ${\ce {CH4}}$ 。
八面体：六个周边原子处在八面体的六个顶点，中心原子位于四面体中心。理想键角90°，例如六氟化硫SF₆。
锥形
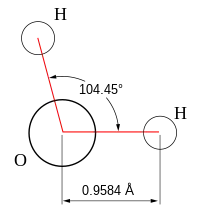
- 三角锥：四面体型的一条键被孤对电子占据，剩下三条键的形状即是三角锥型。由于孤对电子体积较大，三角锥形的键角较四面体形的键角要小。例如氨 ${\ce {NH3}}$ ，键角107.3°。
- 四方锥：八面体型的一条键被孤对电子占据，剩下五条键的形状即是四方锥型，例如五氟化溴 ${\ce {BrF5}}$ 。
角形：与直线型相对，两条键的三个原子不在一条直线上。例如水H₂O，键角104.5°。

除了上述的基本类型外，也存在以下的分子结构：

T形：此分子構型描述其中央原子有著三個配基的化合物形狀，二個鍵位於一直線上，另一個鍵則和上述二個鍵垂直，因此形成T形的結構，例如三氟化氯 ${\ce {ClF3}}$ 。根據價層電子對互斥理論，T形分子構型是三個配基和兩個中央原子的孤電子對相互作用造成的結果。
三帽三角稜柱：分子構型描述有九個原子、原子基團或配基被安排在一個中心原子周圍的形狀，利用三側錐三角柱（一個有著和三個矩形面相接觸的額外原子的三角柱）定義此種分子的頂點。這和帽狀方形反稜柱分子構型非常相似，並且在某些分子中對於此特定的幾何構型展現出一些爭議。九氫合錸(VII)酸鉀中的九氫合錸(VII)酸根離子 ${\ce {ReH_9^2-}}$ 通常被視為擁有三帽三角稜柱分子構型，雖然有時此幾何構型用帽狀方形反稜柱分子構型所取代。
三角稜形：分子構型描述有六個原子、原子基團或配基被安排在一個中心原子周圍的形狀，利用三角柱定義此種分子的頂點。
五角平面：分子構型描述有五個原子、原子基團或配基被安排在一個中心原子周圍的形狀，利用五角型定義此種分子的頂點。
五角錐：分子構型描述有六個原子、原子基團或配基被安排在一個中心原子周圍的形狀，利用五角錐形定義此種分子的頂點。這是有著不均勻鍵角的少數分子鍵的其中一種。
帽狀方形：反稜柱分子構型描述有八個原子、原子基團或配基被安排在一個中心原子周圍的形狀，利用正四角錐反角柱定義此種分子的頂點。正四角錐反角柱是一種有著正四角反稜柱的四角錐去連接到方形的底部。在這方面，這可以被看成「覆蓋的」正四角反稜柱（一個有著錐體豎立在某個方形面的正四角反稜柱）。這和三帽三角稜柱分子構型非常相似，並且在某些分子中對於此特定的幾何構型展現出一些爭議。九氫合錸(VII)酸根 ${\ce {ReH{_{9}}^{2-}}}$ 有時被視為擁有帽狀方形反稜柱分子構型，雖然有時她的幾何構型用三帽三角稜柱分子構型所取代。
扭曲或覆蓋孤電子對的八面體：分子構型描述有六個原子、原子基團或配基被安排在一個中心原子周圍的形狀（有著一電子對覆蓋著八面體），利用兩個倒立相連的三角錐形定義此種分子的頂點。這種形狀有著分子對稱性。
方形反稜柱分子構型：有八個原子、原子基團或配體連接在一個中心原子周圍的分子構型，其分子形狀類似正四角反稜柱。像八氟合氙(VI)酸亞硝醯 ${\ce {(NO)2XeF8}}$ 中的八氟合氙(VI)酸根離子 ${\ce {XeF_8^{2-}}}$ 離子即為此構型。
蹺蹺板形：或稱蝴蝶骨型，是一種和中央原子有四個鍵結並擁有C2v對稱性的分子構型，名稱"蹺蹺板"的來源是因為其在觀察中看起來像蹺蹺板。和中央原子有四個鍵結的構型中，最常見的為四面體，或是較少見的，方形平面構型，所以蹺蹺板形分子構型就像他的名字一樣，是很少見的。

**价层电子对互斥理论**
鍵連原子	孤對電子	電子對數	形狀	理想鍵角	例子
2	0	2	直線形	180°	CO₂
3	0	3	平面三角形	120°	BF₃
2	1	3	角形	120° (119°)	SO₂
4	0	4	四面體形	109.5°	CH₄
3	1	4	三角錐形	107°	NH₃
2	2	4	角形	109.5° (104.5°)	H₂O
5	0	5	三角雙錐形	90°, 120°, 180°	PCl₅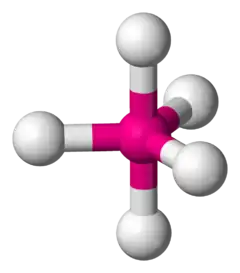
4	1	5	變形四面體形	180°, 120°, 90° (173.1°, 101.6°)	SF₄
3	2	5	T字形	90°, 180° (87.5°, < 180°)	ClF₃
2	3	5	直線形	180°	XeF₂
6	0	6	八面體形	90°, 180°	SF₆
5	1	6	四角錐形	90° (84.8°), 180°	BrF₅
4	2	6	平面四方形	90°, 180°	XeF₄
7	0	7	五角雙錐形	90°, 72°, 180°	IF₇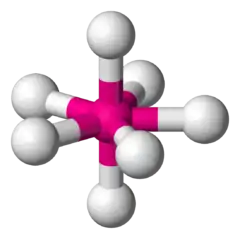
6	1	7	五角錐形	72°, 90°, 144°	XeOF₅⁻
5	2	7	平面五角形	72°, 144°	XeF₅⁻
8	0	8	四方反稜柱形		XeF₈²⁻
9	0	9	三側錐三角柱形		ReH₉²⁻
10	0	10	雙四角錐反角柱		Th(C₂O₄)₄²⁻ [4]
11	0	11	五角錐反角柱		[Th^IV(NO₃)₄(H₂O)₃] [4]
12	0	12	二十面體		Mg[Th(NO₃)₆].8H₂O 裡的 Th(NO₃)₆²⁻離子[5]

参考文献

McMurry, J. (1992). Organic Chemistry (3rd Edn.), Belmont:Wadsworth. ISBN 0-534-16218-5
Cotton, F. Albert; Wilkinson, Geoffrey; Murillo, Carlos A.; Bochmann, Manfred (1999). Advanced Inorganic Chemistry (6th Edn.) New York:Wiley-Interscience. ISBN 0-471-19957-5.
Alexandros Chremos; Jack F. Douglas. . J. Chem. Phys. 2015, 143 (11): 111104. Bibcode:2015JChPh.143k1104C. PMID 26395679. doi:10.1063/1.4931483 .
Greenwood, N. N.; Earnshaw, A. 2nd. Oxford:Butterworth-Heinemann. 1997. ISBN 0-7506-3365-4.
Wells A.F. (1984) Structural Inorganic Chemistry 5th edition Oxford Science Publications ISBN 0-19-855370-6

参见

外部链接

共价键和分子结构（页面存档备份，存于）
超分子形状（页面存档备份，存于）（蛋白质、DNA和RNA）http://swift.cmbi.ru.nl/（页面存档备份，存于）
3D化学（页面存档备份，存于）——化学，结构和3D分子
IUMSC——印第安纳州大学分子结构中心
分子结构

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] McMurry, J. (1992). Organic Chemistry (3rd Edn.), Belmont:Wadsworth. ISBN 0-534-16218-5

[2] Cotton, F. Albert; Wilkinson, Geoffrey; Murillo, Carlos A.; Bochmann, Manfred (1999). Advanced Inorganic Chemistry (6th Edn.) New York:Wiley-Interscience. ISBN 0-471-19957-5.

[article0-3] Alexandros Chremos; Jack F. Douglas. . J. Chem. Phys. 2015, 143 (11): 111104. Bibcode:2015JChPh.143k1104C. PMID 26395679. doi:10.1063/1.4931483 .

[Greenwood-4] Greenwood, N. N.; Earnshaw, A. 2nd. Oxford:Butterworth-Heinemann. 1997. ISBN 0-7506-3365-4.

[Wells-5] Wells A.F. (1984) Structural Inorganic Chemistry 5th edition Oxford Science Publications ISBN 0-19-855370-6