利普希茨連續

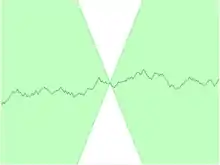
对于利普希茨连续函数，存在一个双圆锥(白色)其顶点可以沿着曲线平移，使得曲线总是完全在这两个圆锥外。

對於在實數集的子集的函數${\displaystyle f\colon D\subseteq \mathbb {R} \to \mathbb {R} }$ ，若存在常數${\displaystyle K}$，使得${\displaystyle |f(a)-f(b)|\leq K|a-b|\quad \forall a,b\in D}$，則稱${\displaystyle f}$ 符合利普希茨條件，對於${\displaystyle f}$ 最小的常數${\displaystyle K}$ 稱為 ${\displaystyle f}$ 的利普希茨常數。

若${\displaystyle K<1}$，${\displaystyle f}$ 稱為收縮映射。

利普希茨條件也可對任意度量空間的函數定義：

給定兩個度量空間${\displaystyle (M,d_{M}),(N,d_{N})}$，${\displaystyle U\subseteq M}$。若對於函數${\displaystyle f:U\to N}$，存在常數${\displaystyle K}$ 使得

${\displaystyle d_{N}(f(a),f(b))\leq Kd_{M}(a,b)\quad \forall a,b\in U}$

則說它符合利普希茨條件。

若存在${\displaystyle K\geq 1}$使得

${\displaystyle {\frac {1}{K}}d_{M}(a,b)\leq d_{N}(f(a),f(b))\leq Kd_{M}(a,b)\quad \forall a,b\in U}$

則稱${\displaystyle f}$為双李普希茨(bi-Lipschitz)的。

若已知${\displaystyle y(t)}$有界，${\displaystyle f}$符合利普希茨條件，則微分方程初值問題${\displaystyle y'(t)=f(t,y(t)),\quad y(t_{0})=y_{0}}$剛好有一個解。

在應用上，${\displaystyle t}$通常屬於一有界閉區間（如${\displaystyle [0,2\pi ]}$）。於是${\displaystyle y(t)}$必有界，故${\displaystyle y}$有唯一解。

• ${\displaystyle f:[-3,7]\to \mathbb {R} ,\quad f(x)=x^{2}}$符合利普希茨條件，${\displaystyle K=4}$。
• ${\displaystyle f:\mathbb {R} \to \mathbb {R} ,\quad f(x)=x^{2}}$不符合利普希茨條件，當${\displaystyle x\to \infty ,\quad f'(x)\to \infty }$。
• 定義在所有實數值的${\displaystyle f(x)={\sqrt {x^{2}+5}}}$符合利普希茨條件，${\displaystyle K=1}$。
• ${\displaystyle f(x)=|x|}$符合利普希茨條件，${\displaystyle K=1}$。由此可見符合利普希茨條件的函數未必可微。
• ${\displaystyle f:[0,1]\to [0,1],\quad f(x)={\sqrt {x}}}$不符合利普希茨條件，${\displaystyle x\to 0,\quad f'(x)\to \infty }$。不過，它符合赫爾德條件。
• 若且唯若處處可微函數f的一次導函數有界，${\displaystyle f}$符合利普希茨條件。這是中值定理的結果。所有${\displaystyle C^{1}}$函數都是局部利普希茨的，因為局部緊緻空間的連續函數必定有界。

• 符合利普希茨條件的函數連續，实际上一致連續。
• 双李普希茨(bi-Lipschitz)函數是單射。
• Rademacher定理：若${\displaystyle A\subseteq \mathbb {R} ^{n}}$且${\displaystyle A}$為開集，${\displaystyle f:A''\to \mathbb {R} ^{n}}$符利普希茨條件，則${\displaystyle f}$幾乎處處可微。[1]
• Kirszbraun定理：給定兩個希爾伯特空間${\displaystyle H_{1},H_{2}}$，${\displaystyle U\in H_{1}}$，${\displaystyle f:U\to H_{1}}$符合利普希茨條件，則存在符合利普希茨條件的${\displaystyle F:H_{1}\to H_{2}}$，使得${\displaystyle F}$的利普希茨常數和${\displaystyle f}$的相同，且${\displaystyle F(x)=f(x)\quad \forall x\in U}$。[2][3]

1. Juha Heinonen, Lectures on Lipschitz Analysis （页面存档备份，存于）, Lectures at the 14th Jyväskylä Summer School in August 2004. （第18頁以後）
2. M. D. Kirszbraun. Uber die zusammenziehenden und Lipschitzchen Transformationen. Fund. Math., (22):77–108, 1934.
3. J.T. Schwartz. Nonlinear functional analysis. Gordon and Breach Science Publishers, New York, 1969.