勒壤得轉換
勒壤得轉換(英語:)是一個在數學和物理中常見的技巧,得名於阿德里安-馬裡·勒壤得(Adrien-Marie Legendre)。该操作是一个实变量的实值凸函数的对合变换。它经常用于经典力学中从拉格朗日形式到哈密顿形式的推导、热力学中热力学势的推导以及多变量微分方程的求解。
概述
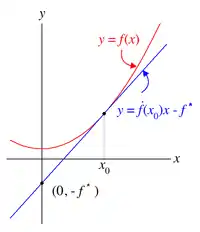
為了研究一個系統內部蘊藏的數學結構,表述此系統的函數關係 改用一個新函數 來表示,其變數 是 的導數, 。而 的值是如右圖藍線在 y 軸的负截距
換句話說,從 x 值到 y 值的函數,轉換成 f(x) 在 x 點的導數到在 x 點切線 y 截距的函數
這程序是由阿德里安-馬裡·勒壤得所發明的,因此稱為勒壤得轉換。稱函數 為 的勒壤得轉換;
用方程式表示
- 。
此式子表示 中的 u 對 而言是個參數,且參數 u 會滿足 的 。即求算表達式關於變數 的極值。
為方便討論,把討論限定在 為嚴格單調遞增。會有這方程式是因為在 也就是斜率不變的狀況下,對每個而言,所有與曲線相交且斜率為的直線族為 。若令,該直線即是在的切線方程式。把x當作常數並由右圖直接觀察可知,在的情況下,值是最小的,也就是說直線方程式中這部分是最大的,而正好 ,正是原方程式所求的極值。
勒壤得轉換是點與線之間對偶性關係()的一個應用。函數 設定的函數關係可以用 點集合來表示;也可以用切線(在嚴格單調遞增的討論下,切線跟導數p有一對一的關係)集合表示。
定義
给定区间I ⊂ ℝ和凸函数f : I → ℝ,则其勒让德变换为函数f* : I* → ℝ,
当f(x)为凸函数时,这个函数有良好的定义。
不难将勒让德变换推广到定义在凸集X ⊂ ℝn 上的凸函数f : X → ℝ:其变换f * : X* → ℝ为定义在
上的函数
其中表示x*和 x的点积。
从导数的角度理解勒让德变换
对于实轴上具有可逆一阶导数的凸函数,其勒让德变换 的一阶导数与的一阶导数互为反函数,反过来说,这个条件可以给出至多相差一个常数的。
最大值式定義
更詳細地定義勒壤得轉換,為了求得 關於 的最大值,設定 關於 的偏導數為零:
- 。
則
- 。(1)
這表達式必為最大值。因為,凸函數 的二阶导数是負數:
- ;
用方程式 (1) 來計算函數 的反函數 。代入 方程式,即可以得到想要的形式:
- 。
計算 的勒壤得轉換,所需的步驟為:
- 找出导函數 ,
- 計算导函數 的反函數 ,
- 代入 方程式來求得新函數 。
這定義切確地闡明:勒壤得轉換製造出一個新函數 ;其新自變數為 。
反函數式定義
另外一種勒壤得轉換的定義是:假若兩個函數 與 的一階導數是互相的反函數;
- ,
或者,
- ,
則 與 互相為彼此的勒壤得轉換。
依照定義,
- ,
- 。
思考下述運算:
- 。
所以,
- ;
這裏, 。
這答案是標準答案;但並不是唯一的答案。設定
- ,
也可以滿足定義的要求。在某些情況下(例如:熱力勢(),會採用非標準的答案。除非另外註明,此頁面一律採用標準答案。
數學性質
以下討論,函數 的勒壤得轉換皆標記為 。
平移性質
- ,
- 。
反演性質
- 。
線形變換性質
讓 成為一個從 到 的線形變換。對於任何定義域為 的凸函數 ,必有
- ;
這裏, 是 的伴隨算子定義為
- 。
例子
應用
熱力學
在熱力學裏,使用勒壤得轉換主要的目的是,將一個函數與所含有的一個自變數,轉換為一個新函數與所含有的一個新自變數,(此新自變數是舊函數對於舊自變數的偏導數);將舊函數減去新自變數與舊自變數的乘積,得到的差就是新函數。勒壤得轉換可以用來在各種熱力勢()之間作轉換。例如,內能 是外延量()熵 ,體積 ,與化學成份() 的顯函數
- 。
對於 ,函數 (非標準的)勒壤得轉換為焓函數 :
- ,
- 。
一個熵與內含量()壓力的函數。當壓力是常數時,這函數很有用。
對於 ,函數 勒壤得轉換為吉布斯能函數 :
- ,
- 。
對於 ,函數 勒壤得轉換為亥姆霍兹自由能函數 :
- ,
- 。
這些自由能函數時常用在常溫的物理系統。
參閱
- 哈密頓力學
- 切觸幾何
- 正則變換
參考文獻
- Arnold, Vladimir. . Springer. 1989. ISBN 0-387-96890-3.
- Rockafellar, Ralph Tyrell. . Princeton University Press. 1996. ISBN 0-691-01586-4.